A Note on Complete Boolean Algebras

2010-09-05SUNXiangrong

上海第二工业大学学报 2010年4期

关键词：子代数涟水理学院

SUN Xiang-rong

(School of Science, Nanjing University of Post and Telecommunications, Nanjing 210046, P. R. China)

A Note on Complete Boolean Algebras

SUN Xiang-rong

(School of Science, Nanjing University of Post and Telecommunications, Nanjing 210046, P. R. China)

This paper shows that a complete Boolean algebra is atomic if and only if each subalgebra of it is atomic.

complete Boolean algebra; atomic algebra; subalgebra

0 Introduction and preliminaries

In literature [1], an atomless complete Boolean algebra is called simple if it has no proper atomless complete subalgebra, the equivalence of which to rigid and minimal is proved in literature [2]. As the same time, the question of whether a simple complete Boolean algebra exists is raised firstly in literature [2]. In literature [3], a positive answer is given. Similarly, in the note, we will give some results of the complete atomic Boolean algebra as same as the complete atomless Boolean algebra.

It is well known that the properties of complete Boolean algebras correspond to properties of generic models obtained by forcing with these algebras, which the major work on complete Boolean algebra come from. But the ideal of this note comes from locale theory, especially in literature [4].

Recall that a frame or a locale is a complete lattice L, satisfying the infinite distributive law: ∀a∈L,S⊆L, a∧∨S=∨{a∧s:s∈S }

By Pt(L) we mean the set of prime elements of a frame L; a frame L is said to be spatial, if for any a∈L, a=∧{p∈Pt(A)p≥a}. The subframe of Frame L is a subset of it, which is closed under finite meets and arbitrary joins. A subset of complete Boolean algebra that is closed under arbitrary meets and arbitrary joins is called complete subalgebra. A complete Boolean algebra is a frame, the complete subalgebra of which is a subframe. The power set of set B is denoted by P(B). Let↑a={b∈Lb≥a}. All more terminology and notation of locale theory which is not explained here is taken from literature [5]; for general background of complete Boolean algebra, we refer to literature [6].

1 Main Result

Definition 1 A complete lattice L is said to be generated by a set, if there exists a subset B of L, satisfying the following conditions:

(1) Any two elements of L is not compatible (∀a,b∈L , we have nota≥b);

(2) For anya∈L,a=∧{b∈Bb≥a} ;

(3) For anya∈L,b0∈↑a∩B ,a≠∧{b∈Bb≥a,b≠b0}.

Lemma 2 Let L be a complete lattice. L is isomorphic to the power set of a set if and only if it is generated by a set.

Proof ⇒ It is trivially.⇐ Suppose L is generated by B. For anyS⊆P(B), letf(S)=∧S. By the Definition 1(2), f is surjective. In the following we show that f is injective. Assuming there exist S1,S2∈P(B)witha=f(S1)=f(S2). IfS1≠S2, it is no problem to suppose that there exists an element b0∈S1such that b0∉S2and b0≥a, then a=∧{b∈Bb≥a,b≠b0}. It is contradictive to condition (3) of Definition 1.

Lemma 3 Let L be a complete Boolean algebra. For anya∈L, ifa=∧{p∈Pt(L)p≥a}, then for anyp0∈↑a∩Pt(L),a≠∧{p∈Pt(L)p≥a,p≠p0}.

Proof Let a=∧{p∈Pt(L)p≥a,p≠p0}. we have

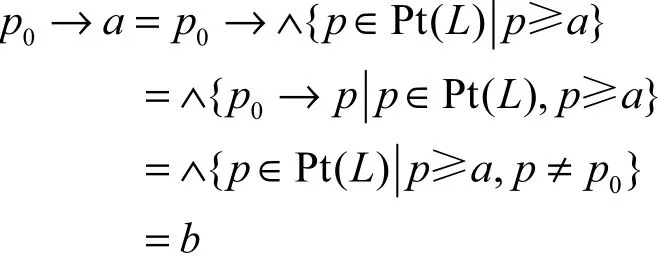
Since L is a Boolean algebra, p0→a=(p0→0)∨a . If b=a, then(p0→0)∨a=a, so p0→0≤a. Butp0≥a, sop0≥(p0→0), contradictorily.

Lemma 4: If L is a spatial complete Boolean algebra, L is generated by Pt(L).

Proof L is spatial, the condition 1 of the definition 1 is satisfied. Since L is a Boolean algebra, the element of Pt(L) is a co-atom, so any two elements Pt(L) are not compatible. The condition 3 can be obtained by Lemma 3.

Theorem 5: If L is a complete Boolean algebra, then the following properties are equivalence:

(1) L is atomic;

(2) L is spatial;

(3) L is generated by a set;

Proof (1)⇔(2) By the duality of Boolean algebras.

(2)⇒ (3) By the Lemma 4.

(3) ⇒ (1) It is trivially.

Remark Some of the theorem can be found in literature [6], here we give an alternative proof of it. Particularly, we pay attention to the property (3). It discovers the essential relation between two elements a and p in L with p∈Pt(L) andp≥a, which is called essence prime in literature [4]. In the following, it plays an important role.

Lemma 6 A subframe of spatial frame is spatial.

Proof Suppose L is a spatial frame, N is a subframe of L. For any p∈Pt(L), letp′=∨{b∈Nb≤p}. Note that p′∈Pt(N), for assuming that there exist two elements x,y∈N with x∧y≤p′, also x∧y≤p, so x≤p or y≤p, moreover, x≤p′ or y≤p′. For anya∈N, we have

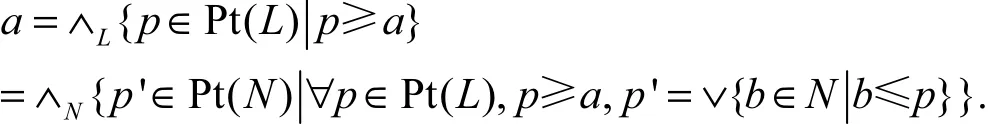
i.e. N is spatial.

Corollary 7 An atomic complete Boolean algebra has no atomicless complete subalgebra.

Lemma 8 Let L be an complete Boolean algebra, each subalgebra of which is atomic. For any a∈L, ifa≠∧{p∈Pt(L)p≥a}, then a is an atom.

Proof Suppose that there exists an element a in L witha≠∧{p∈Pt(L)p≥a,p≠p0}, a is not atomic, then we can find an element b∈L with 0＜ b＜ a. Letb=↑a∪{x→0x∈↑a}, it is easy to verify that B is a proper complete subalgebra of L. SincePt(B)={p∈Pt(L)p≥a}∪{a→0} so B is not spatial. By Theorem 5, B is atomicless, contradictorily.

Lemma 9: Let L be a complete Boolean algebra. For any a∈L, ifa≠∧{p∈Pt(L)p≥a} implies that a is an atom, then L is spatial.

Proof We only need to show that for any atom a∈L,a=∧{p∈Pt(L)p≥a}. Letb=∧{p∈Pt(L)p≥a}. If a≠b, sincea≠∧{p∈Pt(L)p≥a}implies that a is an atom, there no exist element c in L with a ＜ c＜ b. In the following we prove that b→a is prime in L, i.e. a maximal element of L. Assuming we can find an element x in L with (b→a)＜x, also a ＜ x and (b→0)＜x , moreover, b≤x, so x =1, i.e. x is a maximal element of L. Furthermore,(b→a)≥b , so (b→a)∧b=b=a, contradictorily.

Theorem 10: A complete Boolean algebra is atomic if and only if each subalgebra of it is atomic.

[1] JECH T. A propos d'algebres de Boole rigides et minimales[J]. C. R. Acad. Sci. Paris Ser. A, 1972, 274:371-372.

[2] MCALOON K. Les algebres de Boole rigides et minimales[J]. C. R. Acad. Sci. Paris Ser. A, 1971, 272:89-91.

[3] JECH T. A complete Boolean algebra that has no proper atomless complete subalgebra[J]. Journal of Algebra, 1996, 182:748-755.

[4] NIEFIELD S B, POSENTHAL K I. Spatial sublocales and essential primes[J]. Topology and Its Applications, 1987, 26:263-269.

[5] JOHNSTONE P T. Stone Spaces[M]. Cambridge:Cambridge Univ. Press, 1982.

[6] SIKORSKI R. Boolean Algebras[M]. Berlin:Springer-Verlag Press, 1964.

关于完备布尔代数的一点注解

孙向荣
（南京邮电大学理学院，南京210046）

给出了完备布尔代数是原子的等价刻画。同时，证明了一个完备的布尔代数是原子的当且仅当每一个真子代数是原子的。

完备布尔代数；原子；子代数

06D05, 03G05