球面经纬线图的分数色数
2010-09-04夏幼明
高 炜,梁 立,夏幼明
(云南师范大学计算机科学与信息技术学院,云南昆明 650092)
球面经纬线图的分数色数
高 炜,梁 立,夏幼明
(云南师范大学计算机科学与信息技术学院,云南昆明 650092)
图的着色问题是图论的重要研究课题之一,分数色数作为正常色数的一个推广在计算机的许多领域中有着重要的应用.本文给出了球面经纬线图以及它的r-冠图的分数色数,分数关联色数和分数全色数.
分数色数 分数团 球面经纬线图 分数关联色数 分数全色数
与图的分数着色有关的研究最早可以追溯到1970年对图的多重着色的研究.E.R.Scheinerman和D.H.Ullman在文献[1]中有关于此专题的较为详尽的论述.图的分数色数有着十分广泛的应用,例如MWIS问题,相关内容可参考文献[1-3].关于图的分数着色有很多不同的定义方式,下面给出几种最常见也是最重要的定义,即:分数着色,分数团和a:b着色.文中只考虑无向、简单、有限图.文中涉及的符号和标记若没有特别说明,则与文献[4]一致.
1 基本概念和引理

注:定义1.1和定义1.2中S={S1,S2,…,St},其中t=F(G)-1,即t为G的Fibonacci数减1,相关内容可参考文献[5].
定义1.3[6]图G的a:b着色,就是指给G中各顶点分配一个集合{1,2,…,a}的b元子集,使得相邻顶点的集合不交,则χ(fG)=inf{a/b存在a:b着色}.
以上3个定义是等价的,并且图G的分数色数是一个有理数,相关内容可参考文献[6].
定义1.4[7]令k和d是正整数,使得k≥2d,图G=(V,E)的一个(k,d)着色是一个映射c:V(G)→Zk={1,2,…,k},使得对任意的uv∈E(G),k-dc(u)-c(v)d.由此定义图的圆色数χ(cG)=min{k/ d有(k,d)着色}.圆色数又称为星色数,记为χ*(G).若图G满足χ(fG)=χ(cG),则G称为星极图(star-extremal).
定义1.5[8]球面经纬线图由两个顶点u,v(称作两极)和连接u,v的n条经线和球面上的m条纬线构成,记作Cm,n.它的顶点集包括u,v和mn个内点,每条经线是一长度为m+1的连接u,v的路,每条纬线是一长度为n的圈,其中m≥1,n≥3.
定义1.6图G的关联图S(G)是这样一个图:V (S(G))={(v,e)∈V(G),e∈E(G)且v与e在G中关联},顶点(u,e),(v,f)之间存在边当且仅当下列三种情况之一:①u=v;②e=f;③uv=e或uv=f.图G的关联图的色数称为G的关联色数,记为inc(G).用incf(G)表示G的分数关联色数,即G的关联图的分数色数.
定义1.7图G=(V,E)的全图T(G)是这样的图:它的顶点集合为V(G)∪E(G),T(G)中两个顶点之间存在边当且仅当它们在G中相邻或相关联.图G的全图的色数称为G的全色数,记为χ″(G).用χ″f(G)表示G的分数全色数,即G的全图的分数色数.
定义1.8图Ir(G)表示G的r-冠图,它是在图G的每个顶点上都粘接r条悬挂边所得到的图,1-冠图也称为王冠.在G的一个顶点v上粘接的r条悬挂边的端点集记作v*.
引理1.1[4]对阶数为n的完全图Kn有χf(Kn)=n.
引理1.2[4]如果H是G的子图,则χf(H)≤χf(G).
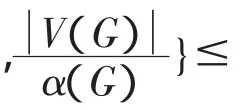
2 主要定理以及证明
本文给出了球面经纬线图以及它的r-冠图的几种分数色数:

由于篇幅有限,这里只给出定理2.2的详细证明过程,用类似的方法可证明定理2.1.
定理2.2证明:
(1)当n为偶数时,一方面Ir(Cm,n)中存在K3,由引理1.1知 χf(K3)=3,再由引理1.2知χf(Ir(Cm,n))≥3.另一方面,在Cm,n中记上往下第j(1≤j≤m)条纬线相对应的n个顶点为 uj1,uj2,…,ujn.对于uji(1≤j≤m,1≤i≤n),若i+j=奇数,则着颜色1.若i+j=偶数,则着颜色2;两极u,v着颜色3.中顶点均着颜色3;u*和v*中顶点着颜色1或2.从而Ir(Cm,n)存在正常3着色,由引理1.3可知χf(Ir(Cm,n))≤3.故有 χf(Ir(Cm,n))=3.
当n为奇数时,构造Ir(Cm,n)的(3n-1):(n-1)着色.对于集合{1,2,…,3n-1},当j为奇数时,顶点uj1,uj2,…,ujn分别分配子集{1,2,…,n-1},{n,…,2n-2},{2n-1,2n,1,2,…,n-3},{n-2,n-1,…,2n-4},…,{n+4,…,2n,1,2},{3,…,n,n+1},{n+2,…,2n}.也就是说,用前2n个元素的集合{1,2,…,2n}循环分配给uj1,uj2,…,ujn.每个顶点分配n-1个元素;当j为偶数时,顶点uj1,uj2,…,ujn分别分配子集{n,…,2n-2},{2n-1,2n,1,2,…,n-3},{n-2,n-1,…,2n-4},…,{3,…,n,n+1},{n+2,…,2n},{1,2,…,n-1};u,v和中顶点均分配{2n+1,2n+2,…,3n-1};u*和v*中顶点可分配{1,2,…,2n}中的任意n-1个元素.由定义,这就是Ir(Cm,n)的(3n-1):(n-1)着色.从而
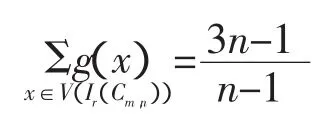
综合上述两方面,当n为奇数时,
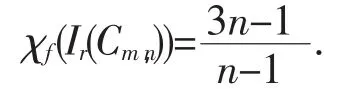
(2)易证
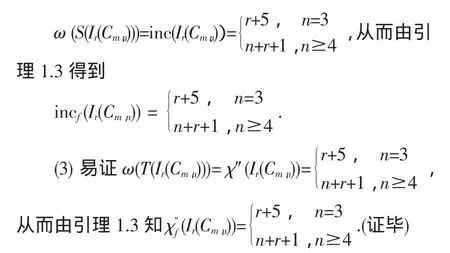
3 一些推论
根据以上得到的结论再结合引理1.3,我们得到如下推论:

注:推论中所述所有图形均为星极图.
[1]高炜,梁立,张超.超图的分数着色研究[J].云南师范大学学报:自然科学版,2009,29(1):33-36.
[2]高炜,梁立,夏幼明.两种特殊冠图的相关分数色数研究[J].西安文理学院学报:自然科学版,2009,12(1):27-30.
[3]Bondy JA,Murty U SR.Graph theory with applications[M].New York:Macmillan Press Lid,1976.
[4]Scheinerman E R,Ullman D H.Fractional Graph Theory[M].New York:John Wiley and Sons,1997.
[5]高炜.随机图的Fibonacci数研究[J].云南师范大学学报:自然科学版,2008,28(1):31-33.
[6]晏静之.关于某些图类的分数色数[D].兰州:西北师范大学,2004.
[7]Vince A.Star Chromatic Number[J].Graph Theory,1988,12:551-559.
[8]冯爱芬,王秀梅,王锋叶.几类特殊图的树宽[J].洛阳师范学院学报,2004(2):7-9.
Fractional C hromatic N umber of M eridian and L atitude L ines on a S phere
GAOWei,LIANG Li,XIA You-ming
(School of Computer Science and Information Technology,Yunnan Normal University,Kunming Yunnan,650092)
The issue of coloring is a very important in the graph theory.Fractional coloring as generalized coloring has used in many fields of computer science.This paper gives formulas to compute the fractional chromatic number、fractional incidence chromatic number and fractional total chromatic number ofmeridian and latitude lines on a sphere and its r-corona graph.
f ractional chromatic number;f ractional clique;meridian and latitude lines on a sphere;f ractional incidence chromatic number;f ractional total chromatic number
TQ92
A
〔编辑 高海〕
1674-0874(2010)01-0012-03
2009-10-13
国家自然科学基金项目[60903131];云南省教育厅科研基金项目[07Z40092]
高炜(1981-),男,浙江绍兴人,硕士,研究方向:图论及其应用.
