求偏导数的一种方法

刘国祥

（赤峰学院 数学学院，内蒙古 赤峰 024000）

求偏导数的一种方法

刘国祥

（赤峰学院 数学学院，内蒙古 赤峰 024000）

计算多元函数的偏导数时，由于变元多，往往计算量大.在求一点的偏导数时，把部分变元的值先代入，再计算偏导数，可以减少运算量.

多元函数；偏导数；高阶偏导数；混合偏导数

计算多元函数的偏导数时，由于变元多，往往计算量比较大.在求某一点的偏导数时，一般的计算方法是，先求出偏导函数，再代入这一点的值而得到这一点的偏导数.我们发现，把部分变元的值先代入函数中，减少变元的数量，再计算偏导数，可以减少运算量.

1 计算方法

例1 设f(x,y)=x2+(x-2)(y-1)arcsin，求和

一般的方法是，先求出偏导函数

再代入偏导数在点(2,1)的值

可以明显地看出第一式中的第二、第三项和第二式中的两项在点(2,1)的值都是0.

这种求偏导数的方法，过程的确很复杂.

现在给出一种比较简单的算法：

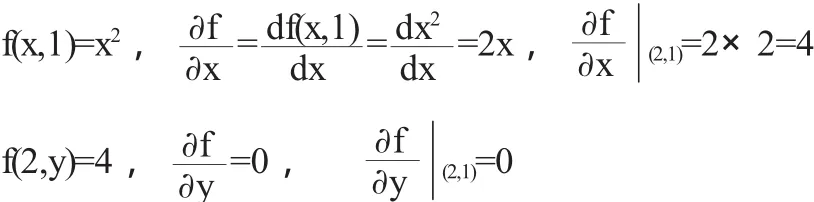
结果与通常的算法一样，但运算量大大减少了.

这种运算方法是：

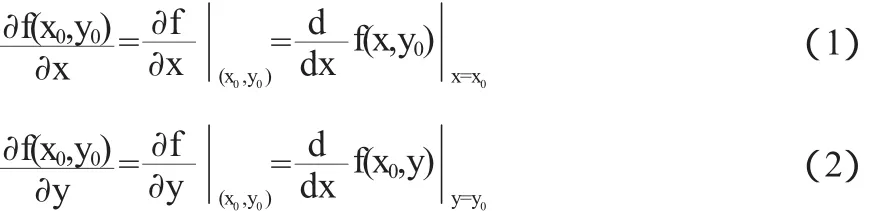
2 计算方法的理论依据

上述算法能够减少运算量的作用是明显的，但可行性的理论依据是什么呢？这不难，从偏导数的定义就可以充分说明.以二元函数为例.

设有二元函数z=f(x,y)，若一元函数f(x,y0)在x=x0处的导数存在，则称它为z=f(x,y)在(x0,y0)处对x的偏导数[1].

这个定义是以一元与多元函数的联系为主线进行的.先代入y=y0的值，成为一元函数再求导数.

设函数z=f(x,y)在点(x0,y0)的某一邻域内有定义，当y固定在y0.而x在x0处有增量△x时，相应地函数有增量f (x0+△x,y0)-f(x0,y0)，如果存在，则称此极限为函数z=f(x,y)在点(x0,y0)处对x的偏导数[2].这个定义与上定义是等价的，其出发点是从极限入手，更突出地强调“y固定在y0”这两个定义都说明求对x的偏导数，可以先把y=y0代入.同理求对y的偏导数，可以先把x=x0代入.

3 在高阶偏导数中的应用

对于高阶偏导数，特别是混合高阶偏导数，由于变元多，求导阶数高，如果函数复杂，运算量会更大.应用上述方法，可以部分地减少运算量.

（一定相等），可以选择求导数的次序，以减少运算量.

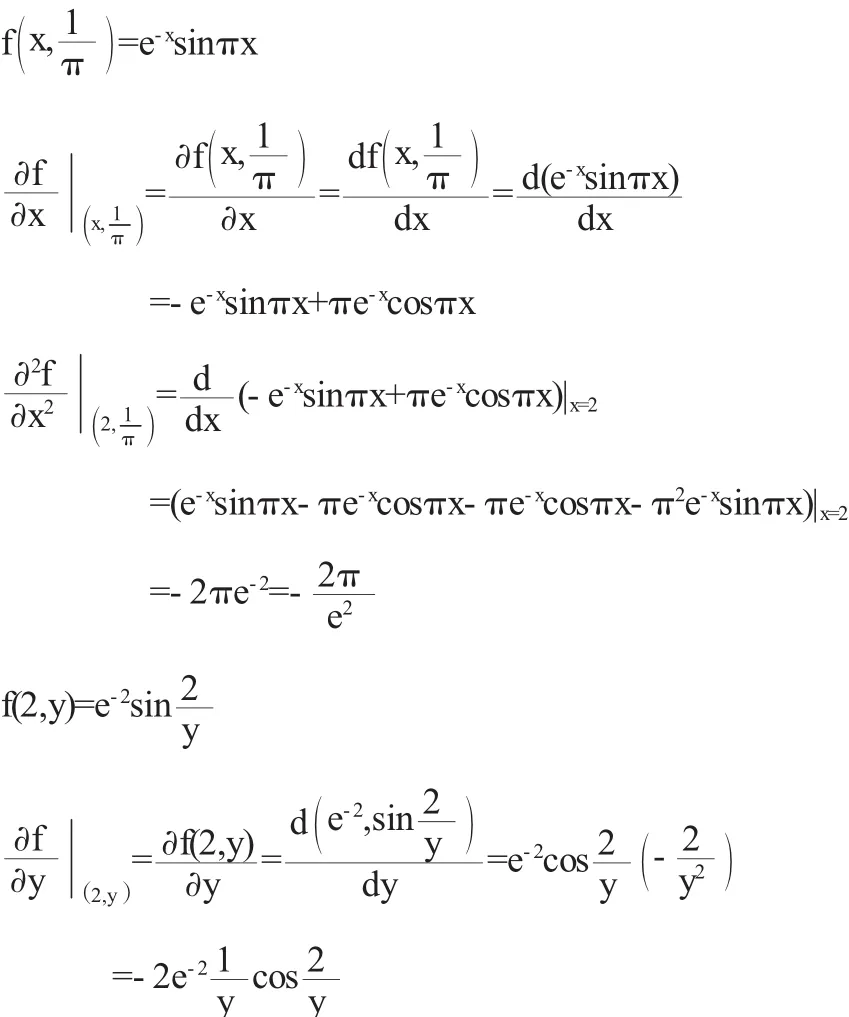
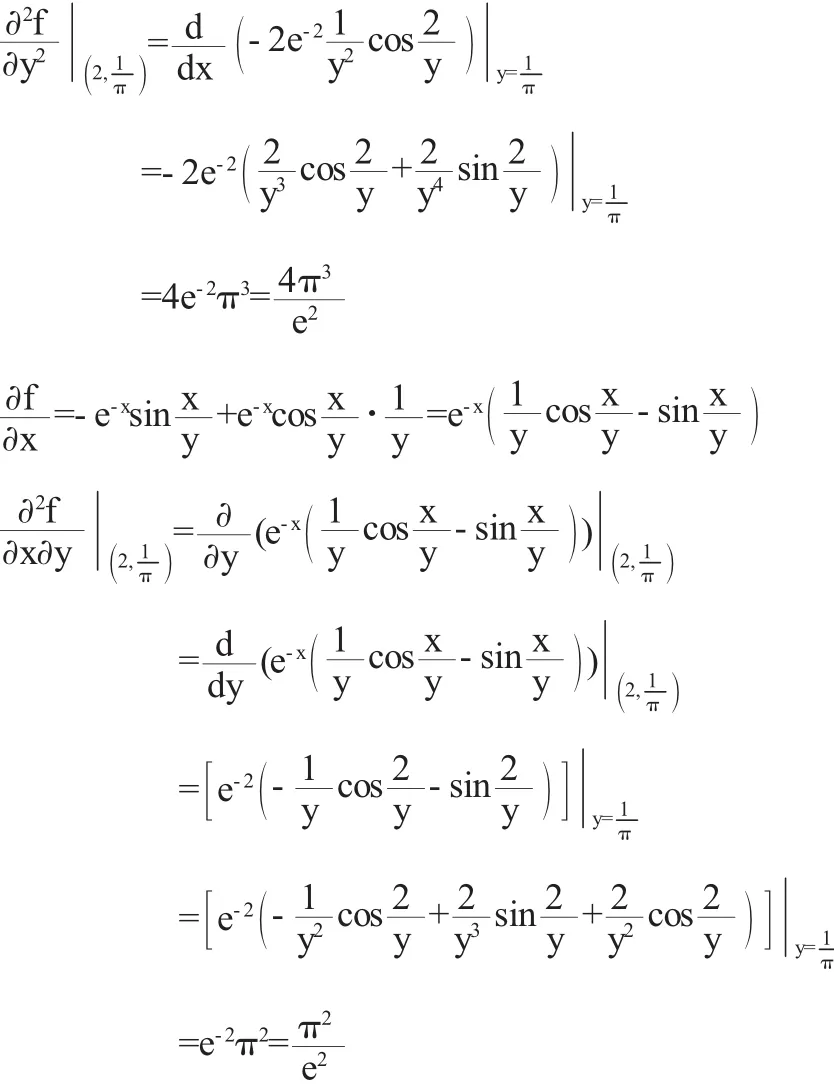
如果换一种顺序，可以

〔1〕范培华，李正元，李永乐.考研数学复习全书.国家行政学院出版社，2006.

〔2〕同济大学数学教研室.高等数学（下册）.高等教育出版社，1996.

O172.2

A

1673-260X（2010）05-0007-02