基于线性特征的机电系统辨识

李 彬，戴 怡

（天津工程师范学院机械工程学院，天津 300222）

基于线性特征的机电系统辨识

李 彬，戴 怡

（天津工程师范学院机械工程学院，天津 300222）

在对不同附加转动惯量的机电系统进行试验的基础上，提出了采用极大似然法进行了系统辨识的方法，并采用Matlab进行仿真，证明该辨识方案的正确性。

机电系统；系统辨识；线性系统

基于非线性模型的高速高精数控机床运动控制是当今控制科学的前沿课题，传统的系统辨识方法在解决非线性系统辨识问题时遇到极大困难。神经网络具有可逼近任意非线性函数的能力，因此可把神经网络作为非线性系统的模型[1-3]。然而神经网络实现技术的现状，使神经网络应用于高速高精数控机床运动控制受到限制[4]。在这种情况下，从工程应用的角度研究基于非线性模型的简化模型——线性模型的控制技术具有实际意义。另一方面，一些实际的高性能数控机床并不主要表现为非线性模型，如高速高精机床加工过程不是处于频繁过零点换向或不总是接近零速时，基于线性模型的控制策略仍是目前情况下的较好选择。本文根据两组试验数据分别进行两个模型的以线性模型为主要特征的系统辨识，并进行了模型的检验与分析。

1 机电系统模型辨识试验

采用松下750 W电机，依据附加转动惯量，采用幅值为3 000的M序列输入信号[5-7]。这样非频繁过零点换向的输入信号，控制对象以线性模型为主要特征。

实验条件：电机采用松下MSMA082C1C，功率750W，额定转速3 000 r/min；驱动器采用松下MSDA083D1A编码器每转脉冲数为2 500 P/r，4倍频反馈，得到编码器每转脉冲数=10 000 P/r；电机控制卡为凌华PCI-8136；工控机采用PentiumⅢ1.3 GHz；附加惯量为1.603 8 kg·cm2。

通过输入正弦信号试验，得到电机系统的最高工作频率fmax=112.15 Hz。作阶跃响应试验，得到电机系统的过渡过程时间Ts=15 ms。设控制器采样间隔周期为1 ms，取M序列的移位脉冲周期Δt=1 ms，M序列循环周期NP=2P-1，得NP=31。实验的输入输出数据见表1。

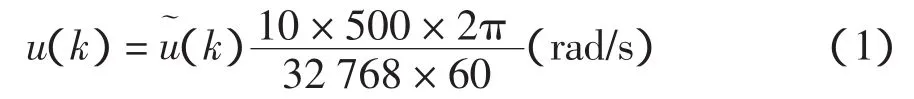
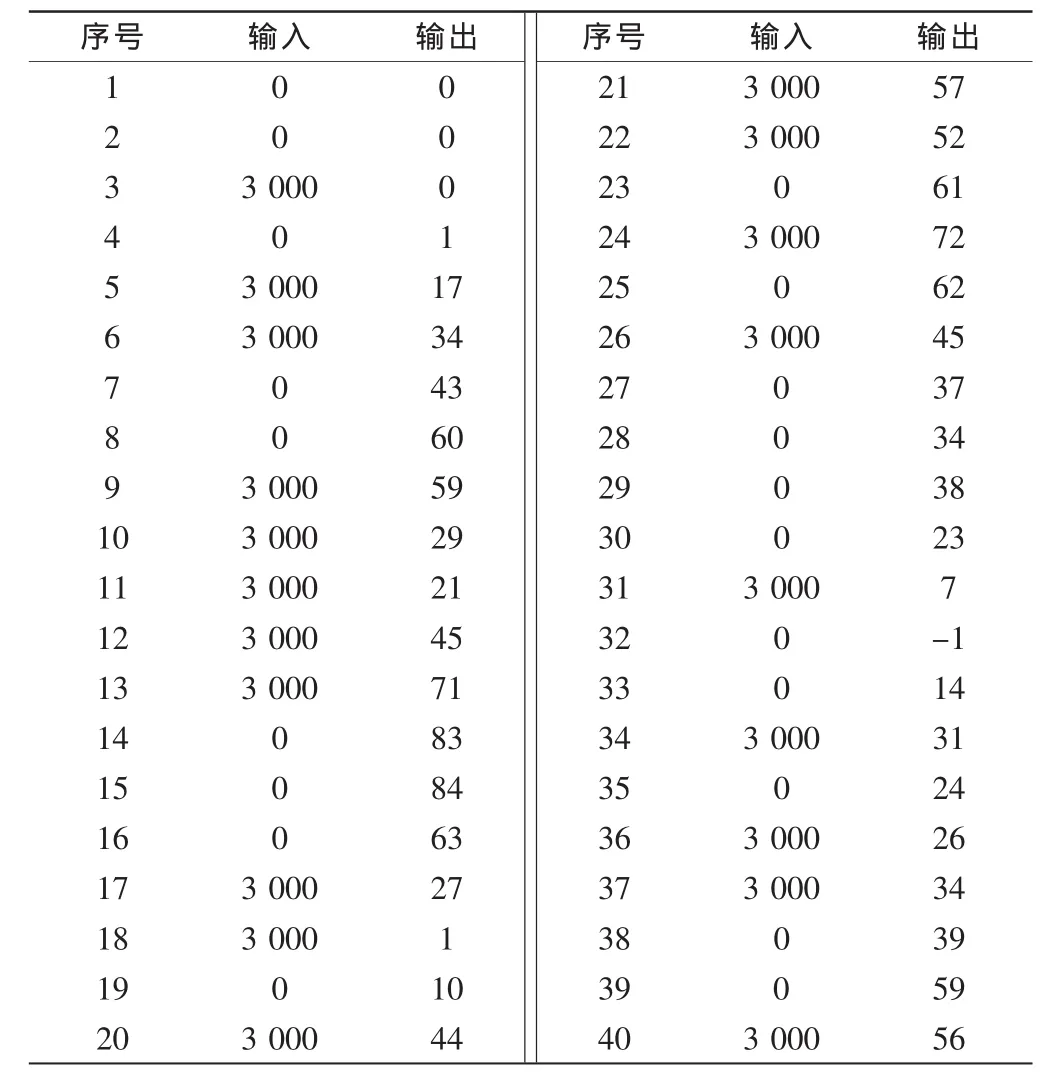
表1 试验输入输出数据

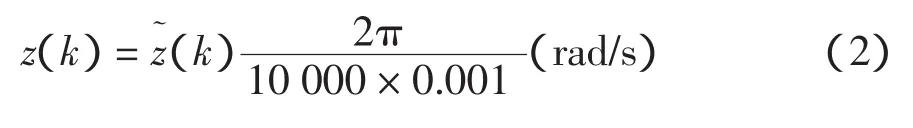
2 系统辨识

2.1 辨识模型选择

对一个给定的单输入、单输出数控系统来说，考虑可辨识性的、规范性的模型结构可采用如下形式：

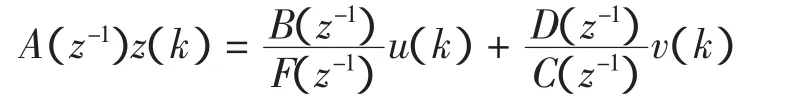
式中：u（k）和z（k）分别为过程的输入输出变量；v（k）为零均值的白噪声。系数多项式为：

模型结构的选择应兼顾灵活性与简洁性，即选用的模型类能比较灵活地描述过程的动态特性，同时模型所用参数应尽可能少。据此选用如下模型：

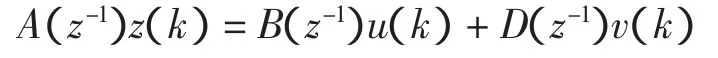
2.2 辨识方法

采用极大似然法进行辨识。就极大似然法来说，它构造一个以数据和未知参数为自变量的似然函数，并通过极大化这个似然函数，获得模型的参数估计值。这意味着模型输出的概率分布将最大可能地逼近实际过程输出的概率分布。

设所研究的模型如图1所示。

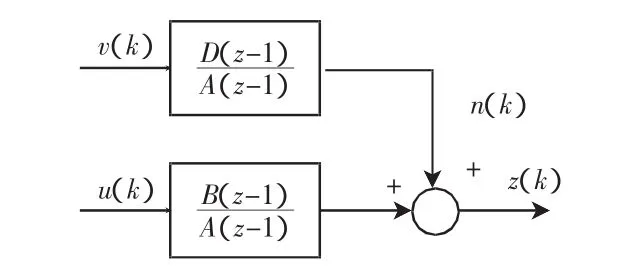
图1 过程的模型表示

其模型为：

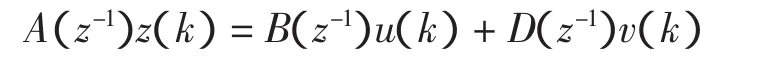
令θ=[a1，a2，…，ana，b1，b2，…，bnb，d1，d2，…，dnd]τ，中间变量为：

递推极大似然参数估计算法可归纳成：

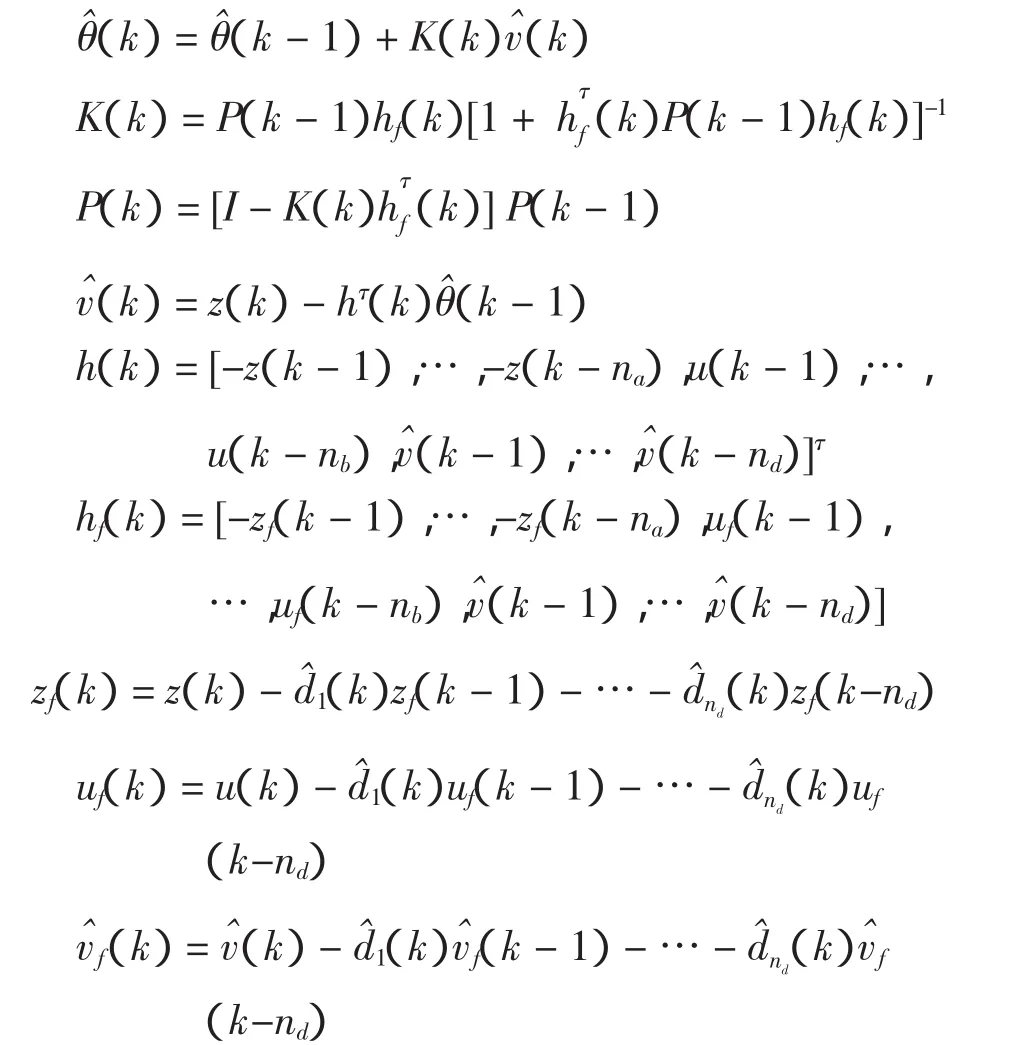
2.3 试验辨识结果

对表1数据，应用极大似然法以及Matlab工具[6]，得到机电系统速度环传递函数如下。

①离散形式：

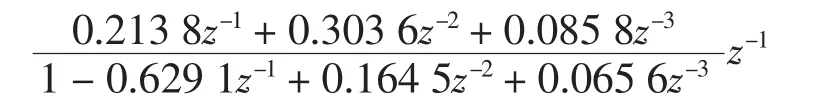
②连续函数的零极点形式：

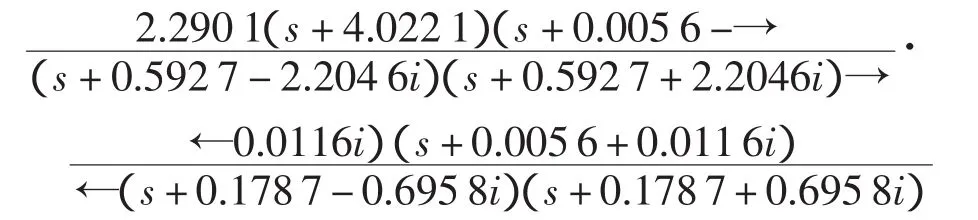
从上式（模型的零极点形式）可以看出，系统的极点的实部全部小于零，因而系统是稳定的。

图2为试验数据的辨识与比较结果。

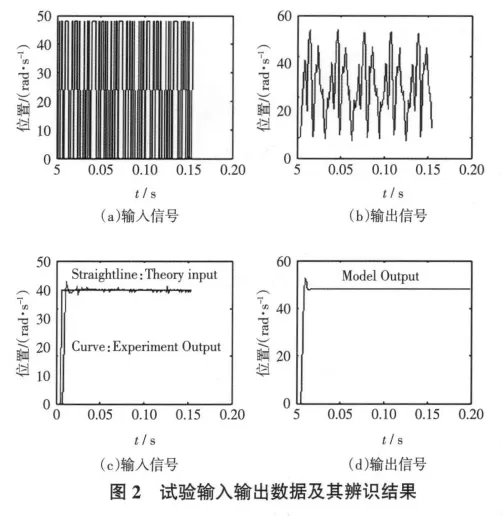
其中，图2（a）是试验输入数据，图2（b）是试验输出数据。由于输出曲线经过零线的次数比较少，相应的Stribeck摩擦力效应也较少，因而非线性摩擦力成分相对较小。图2（c）是试验系统做阶跃输入、输出试验的情况，其中规则的直线是阶跃输入值，参差不齐的曲线是输出值。图2（d）是被辨识模型的阶跃输出，从该图可以看出辨识模型基本正确。

3 模型检验与辨识结果分析

3.1 模型检验方法

设在如下模型类

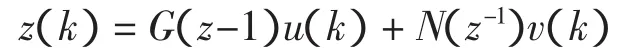
如果输出残差序列{ε（k）}是（或近似是）零均值的白噪声序列，则认为所获得的辨识模型是较好的模型，否则辨识模型可能是不好的模型。这里基于自相关函数检验法进行模型检验。

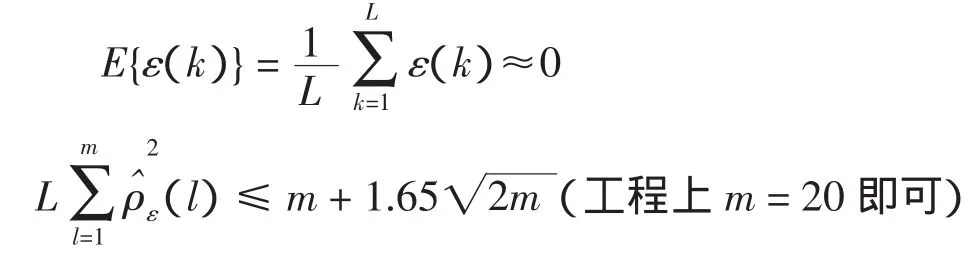
若满足则认为{ε（k）}是零均值的白噪声序列，相应的辨识模型是可靠的，其置信度为95%。

3.2 辨识结果分析

由表1数据，应用极大似然法和Matlab工具，得到计算结果如表2所示。

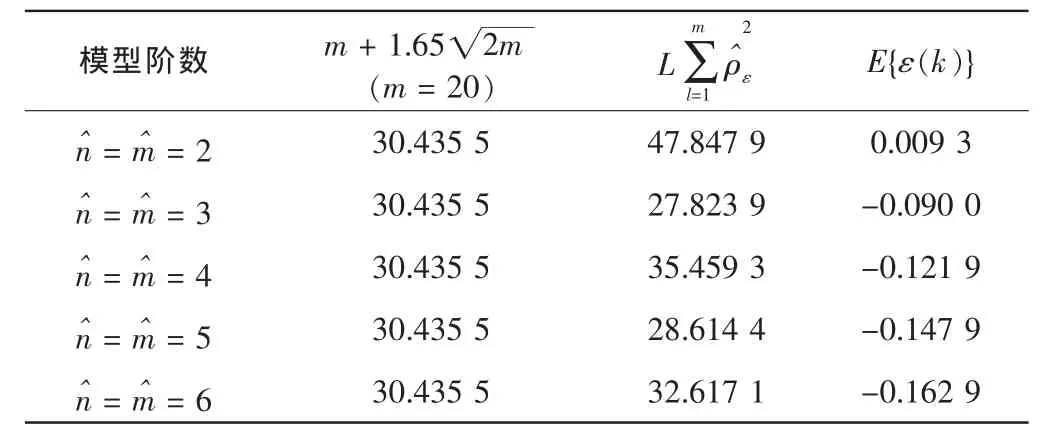
表2 试验辨识结果（仿真模型）模型检验

从表2看出，当取延迟为1个采样周期，模型阶数为3时，辨识结果最好；且当模型阶数为5时，亦有，说明该辨识模型的置信度达到95%。

4 结论

被控对象的离线精确辨识是高速高精数控机床运动控制基础和关键环节。试验系统惯量相对来说大一点，在M序列输入信号作用下，有较少输出信号越过零点，因而此时Stribeck效应的影响较小，系统呈现较小的非线性，所以用线性模型辨识该系统辨识误差较小。

［1］ 吴云洁，刘金琨，王宗学.基于模糊RBF网络的伺服系统辨识及控制[J].计算机仿真，2003（1）：50-53.

［2］ 戴 怡，周云飞.基于IP基本控制回路的预见控制研究[J].天津工程师范学院学报，2005，12（2）：33-36.

［3］ 汪 镭，周国兴，吴启迪.基于Hopfield神经网络的线性系统参数辨识方案及在鼠笼式电机传动系统参数辨识中的应用研究[J].中国电机工程学报，2001（2）：9-11，17.

［4］ 韩 江，屈胜利，王效杰，等.伺服系统辨识的仿真与实现[J].航空计算技术，2005（2）：50-52.

［5］ 许晓峰，王隆太.数控系统被控对象的模型辨识[J].机电产品开发与创新，2006（1）：133-135.

［6］ 戴 怡.高速高精运动控制器技术研究[D].武汉：华中科技大学，2003.

［7］ 谢仕宏.MATLAB R2008控制系统动态仿真实例教程[M].北京：化学工业出版社，2009.

System identification of electromechanical system based on the linear characteristic

LI Bin，DAI Yi
（School of Mechanical Engineering，Tianjin University of Technology and Education，Tianjin 300222，China）

The electromechanical system of additional inertia is tested by using the maximum of likelihood of system identification in this paper.Simulation study through Matlab indicates that the method is promising.

electromechanical system；system identification；linear system

book=2,ebook=1

TM306

A

1673－1018（2010）02－0010－03

2010-01-18

天津市高等学校科技发展基金资助项目（20071107）.

李 彬（1980—），男，硕士，讲师，研究方向为数控技术、故障诊断.