基于能量因子的基因调控网络重构

谭左平, 徐红林, 王士同＊, 堵国成

(1.江南大学信息工程学院,江苏无锡 214122;2.江南大学工业技术教育部重点实验室,江苏无锡 214122)

基于能量因子的基因调控网络重构

谭左平1,2, 徐红林1, 王士同＊1, 堵国成2

(1.江南大学信息工程学院,江苏无锡 214122;2.江南大学工业技术教育部重点实验室,江苏无锡 214122)

重构基因调控网络有助于探索生命系统的本质问题。线性组合模型以其形式简单和易于求解的特点被成功应用于基因网络的重构过程中。作者针对线性组合模型只考虑了基因之间的线性调控关系的缺陷,引入了能量因子的概念,从而使得模型具备了分析基因间的非线性调控关系的特性。将模型应用于大肠杆菌(Escherichia coli)的SOS DNA修复过程中,实验证明:该模型能较好地拟合大肠杆菌的SOS DNA修复过程,进一步提高了调控网络的构建精度。

基因表达;能量因子;调控网络;DNA修复

20世纪50年代DNA双螺旋结构的发现揭开了分子生物学的新时代。自此,在分子水平上研究基因和基因表达,促进了生物学的发展[1]。总的来说,一个基因的表达受其他基因的影响,而这个基因又影响其他基因的表达,这种相互影响相互制约的关系构成了复杂的基因表达调控网络。更一般些,几乎所有的细胞活动都被基因网络所控制[2]。

分子生物学的主要挑战是如何更好地理解基因间的调控机理,基因调控的研究是后基因组时代的核心内容,是系统生物学的主要研究内容,基因调控网络是生命功能在基因表达层面上的展现。基因表达谱可直接检测mRNA的种类及丰度,故可以用来同时分析上万个基因的表达变化,并以此来揭示基因之间表达变化的相互关系[3]。基因调控网络的研究可以通过分析时序基因表达数据,结合生物信息学的方法和技术构建合适的基因调控网络拓扑结构来模拟系统的调控机理,这无疑有助于探索生命系统的本质问题[4]。

目前,通过分析基因表达的微阵列数据,有很多方法和模型被发展和应用于推断基因调控网络。这些研究有助于洞察基因功能和调控关系,理解细胞的生物学功能和工作机理,如布尔网络模型[5-6]、线性组合模型[7]、加权矩阵模型[8]、互信息关联模型、贝叶斯网络模型[9-10]以及微分方程模型[11]。其中线性组合模型是一种最简单的动力学模型,也是较早被用于基因调控网络建模的方法,其最大的优点是原理简单,所构建的网络模型直观易于理解,而且模型的求解相对容易。然而,该模型最大的缺点是只考虑了基因间的线性调控关系,忽略了可能存在的非线性调控关系。

针对这一问题,作者提出了基于能量因子的基因表达调控网络。即在传统的基于线性组合模型的基因调控网络的重构过程中,引入了能量因子的概念,从而在线性组合模型中考虑了基因之间的非线性调控关系。将其应用于E.coli(Escherichia coli)的SOS DNA修复过程,实验结果表明:该模型能够较好的重构E.coli的SOS DNA修复过程中的基因调控网络。

1 基因表达调控网络的重构

1.1 线性组合模型

线性组合模型假定基因之间的相互作用是线性的和非瞬时的,即基因i在时刻tk+1的表达水平是前一时刻tk所有基因j=(j=1,2,L,n)表达水平的加权相加。

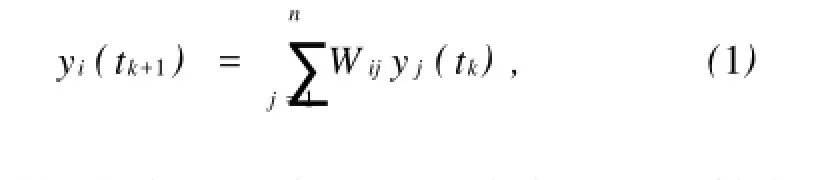
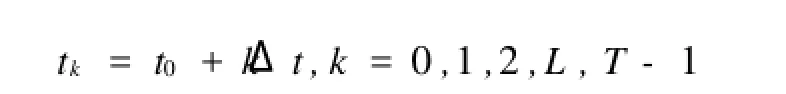
其中,yi(tk+1)代表基因i在tk+1时刻的基因表达水平;Wij表示所有基因j对i基因的调控强度;Δt表示相互作用的平均传递时间。当基因表达时间序列

yi(t)给定,要估计调控网络参数Wij,现称为逆向工程问题(reverse engineering)。即通过寻求网络参数

Wij,使得用线性网络模型拟合原型基因表达时间序列的残差总量达到最小值。

其中,P代表基因的个数;T代表基因的表达时间点。

1.2 能量因子

基因调控网络从生物信息学角度进行研究的前提是:如果两个基因序列谱(gene profiles)相似,则这两个基因协作调控,并可能功能相近;有同样表达模式的基因可能具有同样的表达过程。故在此我们假定,任意两个基因,若其基因表达水平接近,则认为它们可能具有相同的功能,即这两个基因可能属于同一组,从而这两个基因之间的相互影响就比较强。虽然该假设并不一定总是成立,但这在揭示基因调控的重要潜在机制时却很有用。故以下我们引入能量因子(energy factor)的概念:

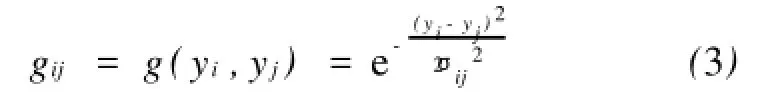
其中yi和yj分别表示为基因i和基因j的表达水平值;σij为方差。当yi和yj之间的差值越小,即基因i和基因j的表达水平越接近,则函数gij的值越大,故基因i和基因j之间的相互影响越大。

1.3 基于能量因子的线性组合模型

将上述的能量影响因子引入传统的线性组合模型中,我们得到一个新的基因表达调控网络模型:

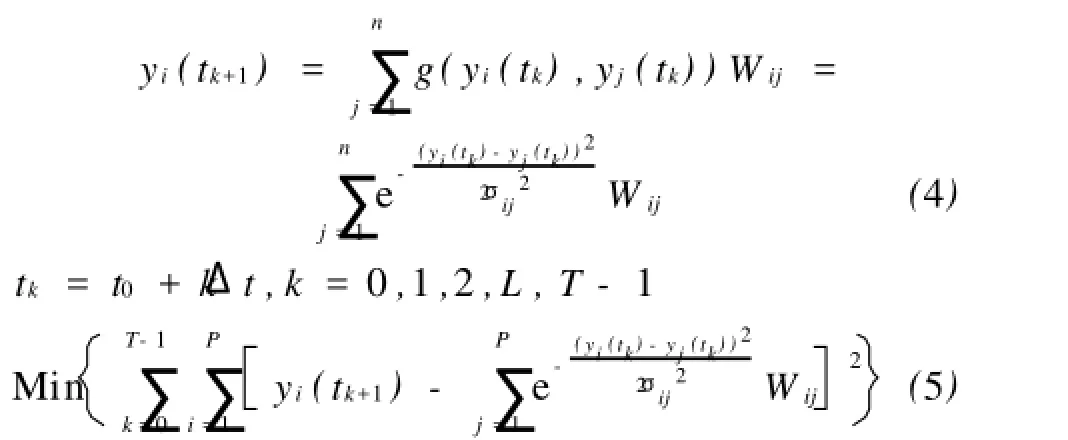
其中yi(tk+1)代表基因i在tk+1时刻的基因表达水平;σij为方差,Wij表示所有基因j对基因i的调控强度;Δt表示相互作用的平均传递时间。P代表基因的个数;T代表基因的表达时间点。

根据式(4)、(5),求得基因调控网络的参数Wij以及σij,使其拟合原型基因表达时间序列的残差总量达到最小值。

2 结果与分析

2.1 大肠杆菌(E.coli)的SOS DNA修复

DNA损伤修复是指在多种酶的作用下,生物细胞内的DNA分子受到损伤以后恢复结构的现象。DNA损伤修复的研究有助于了解基因突变机制,衰老和癌变的原因,还可应用于环境致癌因子的检测。“SOS”是国际上通用的紧急呼救信号(Save Our Souls)。SOS DNA修复是指DNA受到严重损伤、细胞处于危急状态时所诱导的一种DNA修复方式,修复结果只是能维持基因组的完整性,提高细胞的生成率,使细胞有较高的突变率,但留下的错误较多,故又称为错误倾向修复(errorprone repair)。SOS修复一种是能够引起误差修复的紧急呼救修复,是在无模板DNA情况下合成酶的诱导修复,它是SOS反应的一种功能,而SOS反应是DNA受到损伤或脱氧核糖核酸的复制受阻时的一种诱导反应。在大肠杆菌(E.coli)中,这种反应由recA-lexA系统调控。正常情况下处于不活动状态,当有诱导信号如DNA损伤或复制受阻形成暴露的单链时,recA蛋白的蛋白酶活力就会被激活,分解阻遏物lexA蛋白,使SOS反应有关的基因去阻遏而先后开放,产生一系列细胞效应。引起SOS反应的信号消除后,recA蛋白的蛋白酶活力丧失,lexA蛋白又重新发挥阻遏作用,见图1。

图1 大肠杆菌的SOS DNA损伤修复Fig.1 SOS DNA damaged repair ofE.coli

2.2 实验结果

在E.coli的SOS DNA修复过程中,作者考察了8个主要基因之间的相互作用,它们是uvrD, lexA,umuD,recA,uvrA,uvrY,ruvA,polB。本实验所采用的基因表达数据来源于Uri Alon的研究[12]。通过紫外线(UV)照射大肠杆菌,观察大肠杆菌DNA的修复过程,测得上述8个基因在不同的时间点上的表达水平值,见图2。(http://www. weizmann.ac.il/mcb/UriAlon/Papers/SOSData)

根据式(4),重构E.coli基因调控网络模型,并利用PSO算法求解目标函数(详见式(2)),使其拟合原型基因表达时间序列的残差总量达到最小值。PSO算法数学表示如下:

图2 原型基因表达数据(UV=20 J/m2)Fig.2 G ene expression data

设搜索空间为D维,总粒子数为n。向量Xi=(xi1,xi2,L,xiD)为第i个粒子的位置;Pi=(pi1, pi2,L,piD)为第i个粒子“飞行”历史中的最优位置(即该位置对应解最优);向量Vi=(vi1,vi2,L,viD)为第i个粒子的位置变化率(速度)。每个粒子的位置按如下公式进行变化(“飞行”):

其中c1,c2为正常数,称为学习因子;rand()为[0,1]之间的随机数;个体极值pid为粒子本身所找到的最优解,全局极值pgd为整个种群的最优解。第d(1≤d≤D)维的位置变化范围为[-XMAXd,XMAXd],速度变化范围为[-VMAXd,VMAXd],迭代中若位置和速度超过边界范围,则取边界值。

PSO算法的伪代码如下:

While最大迭代数或最小误差未达到

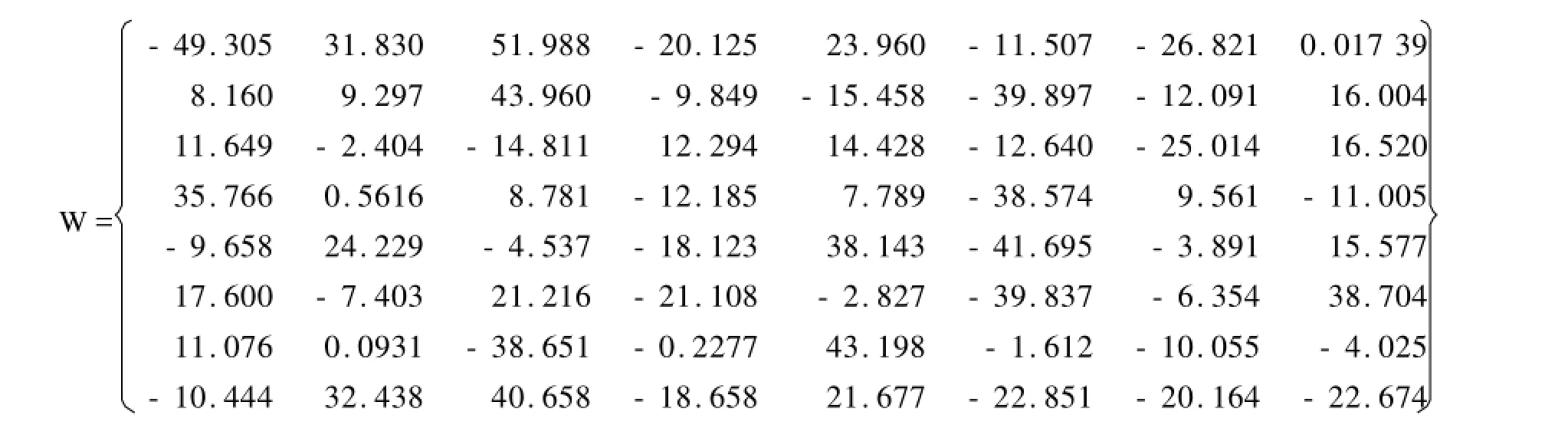
本实验中,粒子群的初始位置和速度随机产生,学习因子c1=c2=2,粒子的位置和速度的变化范围均为[-100,100]。所求得的调控关系矩阵W表示上述8个基因之间的调控水平及相互影响,对于矩阵W中的元素:

若wij>0,则表示基因之间为激励作用;

若wij=0,则表示基因之间无相互影响;

若wij<0,则表示基因之间为阻遏作用。

其具体结果如下所示:

为了更直观的显示结果,我们将所求的调控关系矩阵代入基因网络中进行计算,其详细的实验结果见图3。

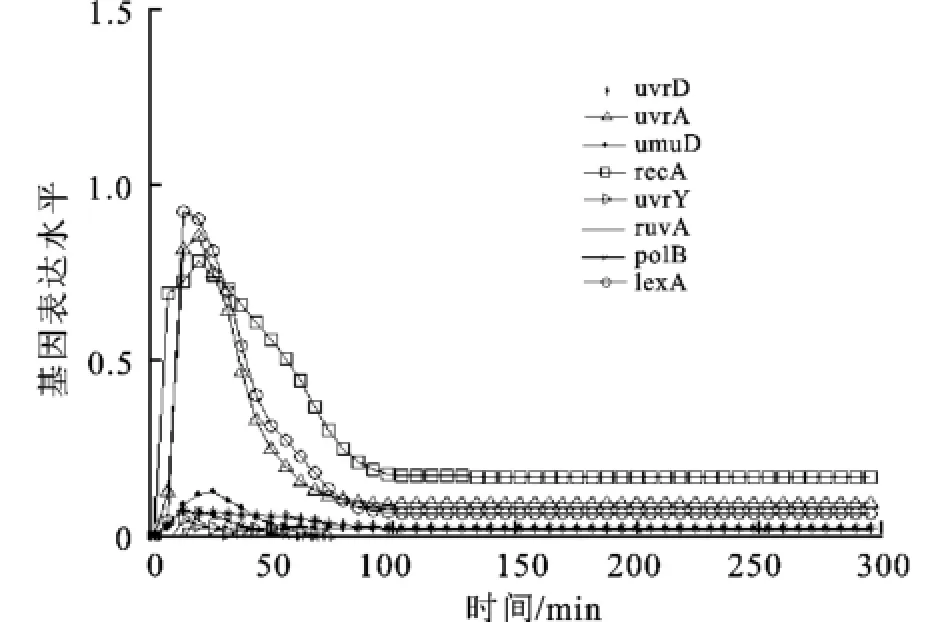
图3 模型拟合结果Fig.3 Result of modeling

从图3中可以看出,8条曲线的大致走向以及变化趋势同拟合原型基本一致,故作者提出的基于能量因子的线性组合模型能够较好的模拟E.coli的SOS DNA修复过程,初步实现了对E.coli的SOS DNA修复过程中8个主要基因之间的调节机制的再现。

3 结 语

基因调控网络是指一组调控因子如何调控一套基因表达的过程,其本质上是一个连续而复杂的动态系统。构建和分析基因调控网络,可以从分子水平认识细胞内的生理活动和功能,对基因之间复杂的调控关系进行解读,从而增进对细胞内调控模式的了解,有助于人们从整体上理解生物学进程[12]。作者采用E.coli的DNA SOS修复过程的基因表达数据,利用基于能量因子的线性组合模型,重构大肠杆菌的DNA SOS修复过程中的基因调控网络,取得了较好的拟合效果。然而,就目前而言,作者尚不清楚转录在分子水平上的所有细节,故根据基因表达数据重构整个基因网络的过程还缺乏生物学理论上的指导,因此,在系统层次上理解调控网络是今后生物信息学要努力解决的问题。

[1]Kanehisa M.Post-Genome Informatics[M].U K:Oxford University Press,2001.

[2]雷耀山,史定华,王翼飞.基因调控网络的生物信息学研究[J].自然杂志,2003,26(1):7-12.

L EI Yao-shan,SHI Ding-hua,WANG Ye-fei.Reviewing the study of gene regulatory networks from bioinformatics[J]. Ziran Zazhi,2003,26(1):7-12.(in Chinese)

[3]许杨,阮琼芳,李燕萍.表达基因分析方法[J].食品与生物技术学报,2008,27(1):122-126.

XU Yang,Ruan Qiong-fang,Li Yan-ping.Analysis methods of expression genes[J].Journal of Food Science and Biotechnology,2008,27(1):122-126.(in Chinese)

[4]崔光照,张勋才,牛云云.重建基因调控网络[J].生物信息学,2007,5(3):125-128.

Cui Guang-zhao,Zhang Xun-cai,Niu Yuan-yuan.Reconstructing transcriptional regulatory networks[J].China Journal of Bioinformatics,2007,5(3):125-128.(in Chinese)

[5]Kauffman SA.Metabolic stability and epigenesis in randomly constructed genetic nets[J].J Theor Biol,1969,22:437-467.

[6]Kauffman S.The lager scale structure and dynamics of gene control circuits:an ensemble approach[J].J Theor Biol, 1974,44:167-190.

[7]Kato M,Tsunoda T,Takagi T.Inferring genetic networks from DNA microarray data by multiple regression analysis [J].G enome Informatics,2000,11:118-128.

[8]Quackenbush J.Computational analysis of microarray data[J].Nat Reviews G enetics,2001,2:418-427.

[9]Friedman N.Inferring cellular networks using probabilistic graphical models[J].Science,2004,303:799-805.

[10]Bickel D R.Probabilities of spurious connections in gene networks:application to expression time series[J].Bioinformatics,2005,21:1121-1128.

[11]Wahde M,Hertz J.Coarse-grained reverse engineering of genetic regulatory networks[J].Biosystems,2000,55:129-136.

[12]Ronen M,Rosenberg R,Shraiman B I,et al.Assigning numbers to the arrows:parameterizing a gene regulation network by using accurate expression kinetics[J].Proceedings of the National Academy of Sciences,2002,99(16):10555-10560.

[13]王明怡,夏顺仁,陈作舟。基于微阵列数据的基因网络预测方法研究进展[J].生物物理学报,2005,21(1):19-25.

WANG Ming-yi,XIA Shun-ren,CHEN Zuo-zhou.Progress on methods for inferring the gene networks from microarray data[J].Acta Biophysics Sinica,2005,21(1):19-25.

(责任编辑:李春丽)

Reconstruction Gene Regulatory Network Depend on by Energy Factor

TAN Zuo-ping1,2, XU Hong-lin1, WANG Shi-tong＊1, DU Guo-cheng
(1.School of Information Technology,Jiangnan University,Wuxi 214122,China;2.Key Laboratory of Industrial Biotechnology,Ministry of Education,Jiangnan University,Wuxi 214122,China)

Reconstruction of gene regulatory network can help to explore the essence of life.The Linear Combination Model has been successfully applied to the reconstruction of the gene regulator network,since it is very simple and can be easily solved.However,the linear relationships between genes were only considered in the model.In order to circumvent this problem,energy factor has been added in the Linear Combination Model,thus the new model can be used to analysis the nonlinear relationships between genes.Then the present model has been applied to reconstruct the gene regulatory network ofEscherichia colion SOS DNA repair process.Our result demonstrated that the proposed model can be reconstruct SOS DNA repair process well and also improve the accuracy.

gene expression,energy factor,regulator network,DNA repair

Q 344

:A

1673-1689(2010)01-0134-05

2009-04-28

国家863计划项目(2006AA10Z313),国家自然科学基金项目(60704047),国家自然科学基金重大研究计划项目(9082002),2008年江苏省普通高校研究生科研创新计划。

谭左平(1981-),女,湖北宜昌人,生物信息学博士研究生。

＊通讯作者:王士同(1964-),男,江苏扬州人,教授,博士生导师,主要从事人工智能、模式识别、模糊系统及生物信息学方面的研究。Email:wxwangst@yahoo.com.cn