构造镶边幻方的代码法

詹 森，王辉丰

（1.广东技术师范学院 计算机科学系，广东 广州 510665；2.海南师范大学 数学与统计学院，海南 海口 571158）

构造镶边幻方的代码法

詹 森1，王辉丰2

（1.广东技术师范学院 计算机科学系，广东 广州 510665；2.海南师范大学 数学与统计学院，海南 海口 571158）

给出构造n=2m+1（m=2，3，…）阶双对称镶边幻方的代码法及其证明，给出构造n= 4m+3（m=1，2，…）阶奇偶镶边幻方的代码法.

双对称；镶边幻方；奇偶镶边幻方；代码法

我们已研究了利用已知的较低阶幻方来构造高阶幻方［1］的方法，也研究了不需要利用已知幻方而直接构造奇数高阶幻方［2-3］的方法，文[4]的镶边法是先构造一个n-2阶幻方，在其中每个方格的数上加同一个整数，然后在它四周镶上一条边，安装入余下来的数字使之成为一个n阶幻方.这种镶边法往往是从已知的、比较容易构造的幻方入手.这里，我们提出一种直接构造镶边幻方的新方法.在讨论新的镶边法之前，介绍几个有关概念如下：

定义1 若一个n=2m+1（m=2，3，…）阶幻方具有以下特性：

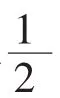
则把以上的n=2m+1（m=2，3，…）阶幻方定义为双对称镶边幻方.m-2个同心子幻方是双对称镶边子幻方.这里采用双对称镶边幻方是避免与对称幻方混淆.

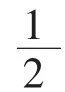
显然，如果若干个自然数其代码之和为零，则表示它们的平均数等于中位数；两个自然数其代码之和为零，就表示它们之和为n2+1，称它们是互为补数.

定义2 若一个n=4m+3（m=1，2，…）阶幻方除具有双对称镶边幻方的全部特性外，其全部奇数都集中于方阵中央的菱形中，而偶数则位于菱形外的四个角.幻方中包含2m个同心的子幻方，其中2m-1个是同心双对称镶边子幻方（是非正规幻方）.则具有这样特性的n=4m+3（m=1，2，…）阶幻方定义为奇偶镶边幻方［4］.

对1～n2中的奇数进行编码，把中位数=（n2+1）的代码规定为0；把奇数-x+2k，x+2（-k）（k=1，2，…，（n2-1））代码分别规定为k，-k.

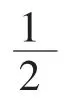
对1～n2中的偶数进行编码，把偶数+（2k-1），-（2k-1）=-x+2（-k）+1（k=1，2，…，（n2-1））的代码分别规定为粗体数字 k，-k，与以上奇数代码区别.

显然，相同数目（t）符号相反的偶数代码（共有2t个）其和为零，就表示它们所表示的偶数的平均数等于中位数.两个偶数其代码之和为零，就表示它们之和为n2+1，称它们是互为补数.两个符号相反的偶数代码之和为r，分别记它们为k1，r-k1，当前者为负后者为正时，它们所表示的偶数分别为+2（k1）+1与+2（r-k1）-1两个偶数之和为+2r.当前者为正后者为负时，结果相同.同理，相同数目（t）符号相反的偶数代码（共有2 t个）其和为r，它们所表示的偶数之和就是2 t+2 r.

以代码为元素的方阵称为代码方阵，简称代方阵，其元素简称为代元.

1 n=2m+1（m=2，3，…）阶双对称镶边幻方的构造方法

第一步 设待安装的n=2m+1（m=2，3，…）阶方阵为A，以a（i，j）（i，j=1，2，…，n）表示A的位于第i行，第j列的元素，按以下规则由中心向外即按k由小到大的顺序安装方阵A的各个元素：

a（m+1，m+1）=0；

第m+1-k（k=1，2，…，m）列a（m+1-k+ h，m+1-k）=（2k2+k）-h（h=0，1，…，k-1）；a（m+1，m+1-k）=-2k2；a（m+1+k-h，m+ 1-k）=-（（2k2-k）-h）（h=0，1，…，k-1）；

第m+1-k（k=1，2，…，m）行a（m+1-k，m+1-h）=-（（2k2+2k）-h）（h=0，1，…，k-1）；a（m+1-k，m+1-k）=2k2+k；a（m+1-k，m+1+h）=2k2-h（h=1，2，…，k）.

此时，只是安装了方阵A左上角（由左下角至右上角对角线以及其上方）的元素，接着，在双对称的位置上安装相应的互补数，就得以代码为元素的代方阵A.代方阵A以及其任一个以0为中心的子方阵，它们的每行、每列和两条对角线上的代码之和都等于0，且具有双对称性.

第二步 把代方阵A中的代码换成其所表示的自然数，得到一个新的n=2m+1（m=2，3，…）阶方阵就是所求的双对称镶边幻方（见定理的证明）.按以上步骤安装幻方的方法称为代码法.

定理 由代码法得出的方阵是一个n=2m+ 1（m=2，3，…）阶双对称镶边幻方.

证明 在代方阵A的以0为中心的任一个2k+ 1（k=1，2，…，m）阶子方阵左上角（由左下角至右上角对角线以及其上方）中，代方阵A的第m+1-k（k=1，2，…，m）列元素之和为

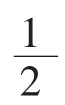
注记 我们的代码法亦可用于文[4]已有的镶边法中的镶边.

2 n=4m+3（m=1，2，…）阶奇偶镶边幻方的构造方法

设待安装的n=4m+3（m=1，2，…）阶方阵为A，以a（i，j）（i，j=1，2，…，n）表示A的位于第i行，第j列的元素.方阵A中央的菱形中所包含的最大方阵是2m+1阶以奇数代码为元素的方阵，我们称为待安装方阵 的2m+1阶基方阵.而低于 2m+1（m≠1）阶方阵是幻方常数为零的双对称镶边子幻方（是非正规幻方）；特别是，当m= 1时，方阵是一个幻方常数为零的双对称的子幻方（是非正规幻方）.

第一步 奇数代码的安装.

a（2m+2-k+h，2m+2-k）=

（2k2+k）-h（h=0，1，…，k-1），

a（2m+2，2m+2-k）=-2k2，

a（2m+2+k-h，2m+2-k）=

-（（2k2-k）-h）（h=0，1，…，k-1）.

代方阵A的第2m+2-k（k=1，2，…，m）行，可取

a（2m+2-k，2m+2-h）=

-（（2k2+2k）-h）（h=0，1，…，k-1），

a（2m+2-k，2m+2-k）=2k2+k，

a（2m+2-k，2m+2+h）=

2k2-h（k=1，2，…，k）.

第二步 偶数代码的安装.

首先，安装菱形外对角线上的偶数代码，再安装第一列的偶数代码，最后，安装其他位置上的偶数代码.在这个过程中，按我们的双对称规则在双对称的位置上安装相应的互补数.

若某行奇数代码之和为正数2r，则同一行左侧对角线上偶数的代码取为-（r+1），右侧对角线上偶数的代码取为-r.若该行有t个奇数代码，则它们所表示的奇数之和为+2（2r），而同一行中对角线上两个偶数代码所表示的偶数之和为

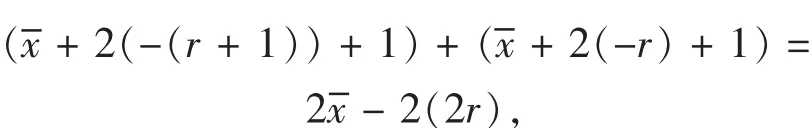
所以，它们所表示的t个奇数和两个偶数的平均数等于中位数.接着，在双对称的位置上安装相应的互补数，至此，已安装了菱形外全部对角线上的偶数代码.

2）安装第一列的偶数代码.

因为取a（1，2m+2）=2（2m+1）（m+1），第一行只有这一个元素是奇数代码，按以上安装菱形外基方阵上方位于对角线上的偶数代码的规则，有

a（1，1）=-（（2m+1）（m+1）+1），

a（1，n）=-（2m+1）（m+1），

所以，对于第一列，我们已有奇数代码a（2m+ 2，1）=2（2m+1）（m+1）-1，偶数代码a（1，1）= -（（2m+1）（m+1）+1）及由双对称规则得到的偶数代码a（n，1）=（2m+1）（m+1），其所表示的奇数是

偶数是

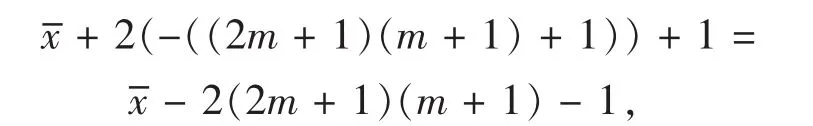
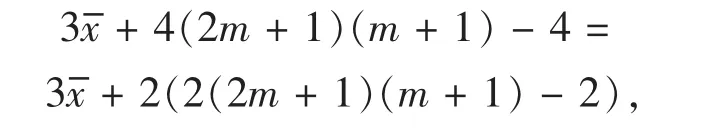
所以，安装第一列其他4m个偶数代码时要有2m个偶数代码是正的，另外2m个偶数代码是负的，且这些偶数代码的和为-（2（2m+1）（m+1）-2）.第一列4m+3个代码所表示的一个奇数和4m+2个偶数的平均数等于中位数.这些偶数代码是从安装于菱形外全部对角线上的偶数代码后剩余下的偶数代码中选取的.

3）安装第2列至第m+1列的代码.

若代方阵A的第s（s=2，3，…，m+1）行位于对角线上的两个偶数代码是-（r+1）和-r，则第s（s= 2，3，…，m+1）列位于对角线上的两个偶数代码是-（r+1）和r，其所表示的偶数分别是-x+2（-（r+ 1））+1=-2r-1和-x+2r-1，它们的和为2-x-2.又由奇数的安装知，该列奇数代码的和为1，若该列有t个奇数代码，该列奇数代码所表示的奇数之和是t-x+2，所以，这些奇数和同一列对角线上两个偶数的平均数等于中位数.所以，上下两对角线之间菱形之外偶数代码（显然，每行都有偶数个）的安装，只要符号相反的偶数代码个数相同且这些偶数代码的和为0即可，而这是很容易做到的.当这一步结束后，基方阵外左方位于两条对角线中间（包括对角线）各列代码所表示的奇偶数的平均数都等于中位数.接着，按我们的双对称规则在基方阵外右方双对称的位置上安装相应的互补数.

第三步 将上述代方阵A中的代码换成其所表示的奇偶数，得到新的n=4m+3（m=1，2，…）阶方阵就是所求的奇偶镶边幻方.

由于整个安装过程是在保证待安装的方阵以及其任一个同心的子方阵都是幻方的前提下，并按双对称规则进行的，所以，当代方阵A安装代码结束并把代码换成其所表示的奇偶数后，显然整个方阵以及其任一个同心的子方阵都是幻方，且具有我们所要求的特性.即这样的方阵是奇偶镶边幻方.

在用代码法构造幻方的每一环节，我们都已经同时给出论证，按我们的安装规则所得到的必定是奇偶镶边幻方.但奇偶数代码的选择、安装具有很大的随意性，及任意以对角线元素为端点的两双对称行（或列）的互换并不导致任何特性的改变，所以，利用这个方法可得出许多不同的奇偶镶边幻方.

由于奇偶镶边幻方自10世纪阿拉伯数学家Alib Almad Al-Antaki［4］构造出11阶奇偶镶边幻方以来，至今未见有人给出此类幻方的构造方法，可见问题有相当的难度.为了读者更好理解以上提出的代码法，这里介绍一个15阶奇偶镶边幻方.为了避免赘述起见，主要给出基方阵的构造过程以及代方阵A，奇偶镶边幻方.

图1 7阶基方阵Fig.1 7-order Basic matrix square

将代方阵A中的代元全部换为相应的奇偶数（略），就得到15阶奇偶镶边幻方A（见图3）.

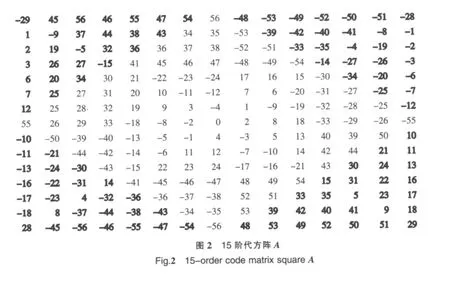
［1］詹森，王辉丰.关于构造高阶幻方的新方法[J].海南师范大学学报：自然科学版，2009，22（3）：133-134.

［2］詹森，王辉丰.奇数阶对称完美幻方的构造方法[J].海南师范大学学报：自然科学版，2009，22（4）：396-398.

［3］王辉丰，詹森.关于构造三类奇数阶幻方的新方法 [J].海南师范大学学报：自然科学版，2010，23（1）：12-15.

［4］吴鹤龄.幻方及其他[M].北京：科学出版社，2004：50-80.

责任编辑：黄 澜

The Code Methods about Structure Bordering Magic Square

ZHAN Sen1，WANG Huifeng2
（1.Department of Computer Science，Guangdong Technical Normal University，Guangdong 510665，China；2.College of Mathematics and Statistics，Hainan Normal University，Haikou 571158，China）

The neWstructure methods called code method were given，which could obtain a n=2m+1（m=2，3，…）order double symmetrical bordered magic square and a lot of n=4m+3（m=1，2，…）order odd-even-bordeved magic squares.Ten former method was proved.

double symmetrical；bordered magic square；odd-even-bordered magic square；code method

O 157.6

A

1674-4942（2010）02-0152-06

2010-01-08