kdv方程的显式行波解
2010-09-11赵长海
赵长海
(南通大学理学院,江苏 南通 226007)
kdv方程的显式行波解
赵长海
(南通大学理学院,江苏 南通 226007)
给出一种求解非线性发展方程精确行波解的新方法:双函数法.使用此方法,借助计算机代数系统Mathematica,利用双函数法和吴文俊消元法,获得kdv方程的多组新的显式行波解,包括孤波解和周期解.
双函数法;吴文俊消元法;kdv方程;行波解
非线性kdv方程现已成为数学物理的基本方程之一,kdv方程最初应用于浅水波的研究.随后相继都引出kdv方程,如文[1-3]用齐次平衡法和椭圆函数法得到了kdv方程的一组解,文[4]和[5]用散射反演法给出了kdv方程的单孤子解和双孤解,文[6]和[7]由试探函数法为kdv方程的求解给出了新的思路.文[8]给出了kdv方程的一个差分格式,由于非线性方程问题的复杂性和特殊性,非线性方程没有统一的求解办法,因而出现求解非线性方程的各种方法,所有这些方法都有一定的局限性.
本文借助Mathermatica软件,采用双函数法和吴文俊消元法[9-12],获得了非线性发展方程kdv的多组行波解.
1 kdv方程的行波解
kdv方程可表示为:

现在用双函数法来求解上述kdv方程,为了求解方程(1),可以先设行波解,令

代入方程(1)可得常微分方程:
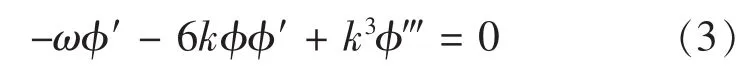
对(2)式积分一次,并取积分常数为零,可得:
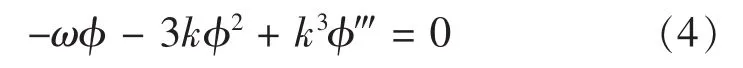
方法1:
由双函数法设方程(4)有如下形式的行波解
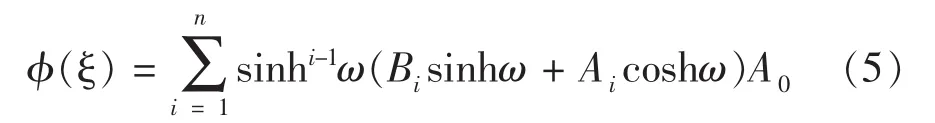
并且通过平衡方程(4)线性最高阶导数项和非线性的次数易知n为2所以,
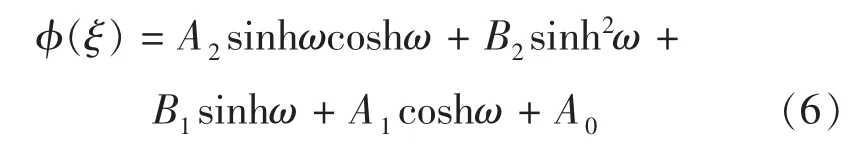
其中 A0,A1,A2,B1,B2为待定系数,而可以有多种选法,令

将(6),(7)代入(4)式,并令其中的常数项以及各次项的系数为零,得到如下线性方程组:
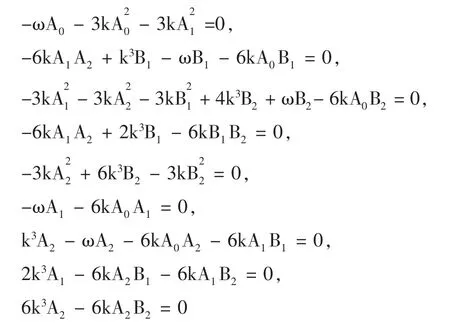
利用吴消元法解上述关于 A0,A1,A2,B1,B2的超待定代数方程组得:
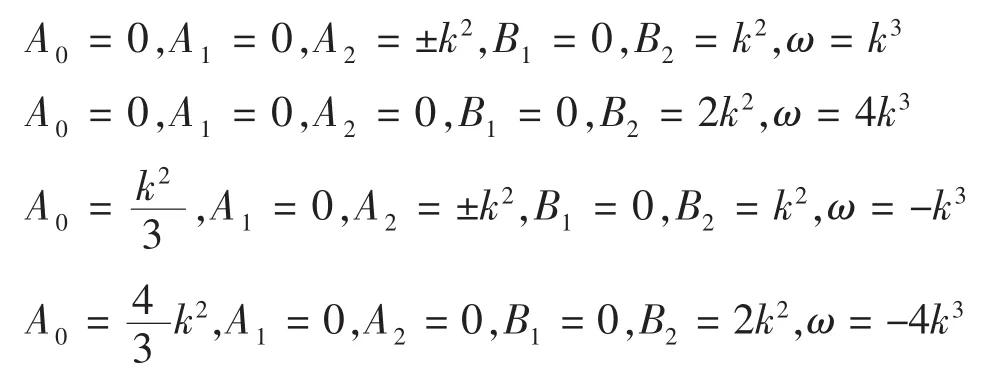
对(7)式分离变量并且两边积分,积分常数取为零得:
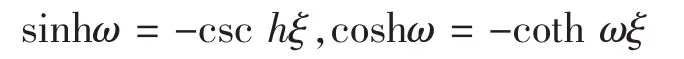
于是方程(4)有如下形式的解

进一步由(2)式可得方程(1)的解为:
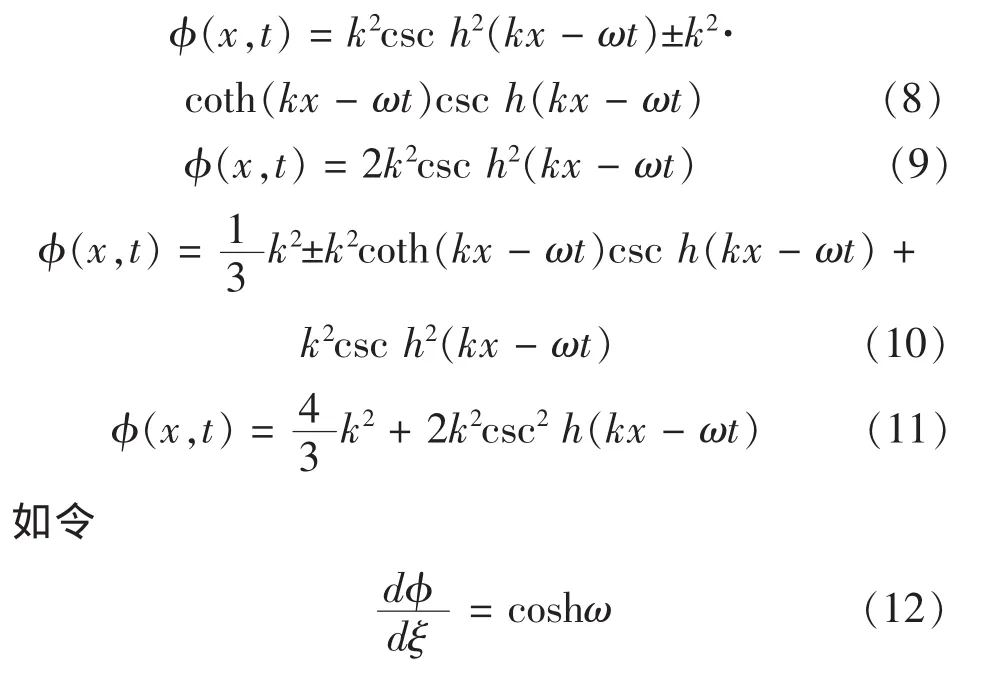
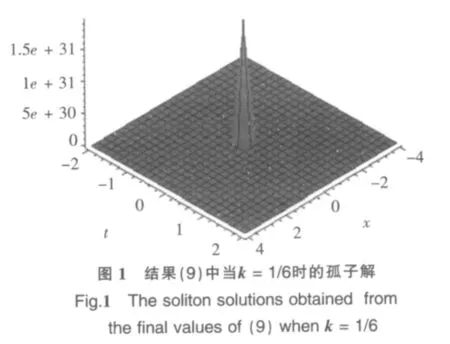
将(6),(12)代入(4)式,并令其中的常数项以及各次项的系数为零,得到如下线性方程组:
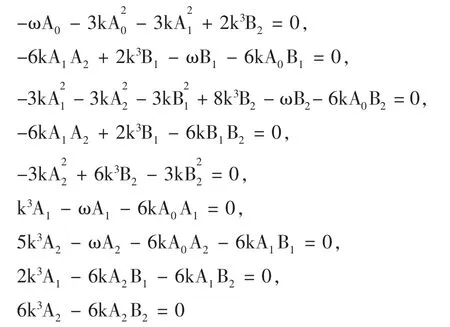
利用吴消元法解上述关于 A0,A1,A2,B1,B2的超待定代数方程组得:

对(12)式分离变量并且两边积分,积分常数取为零得:
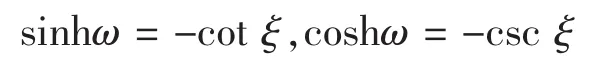
于是方程(4)有如下形式周期解
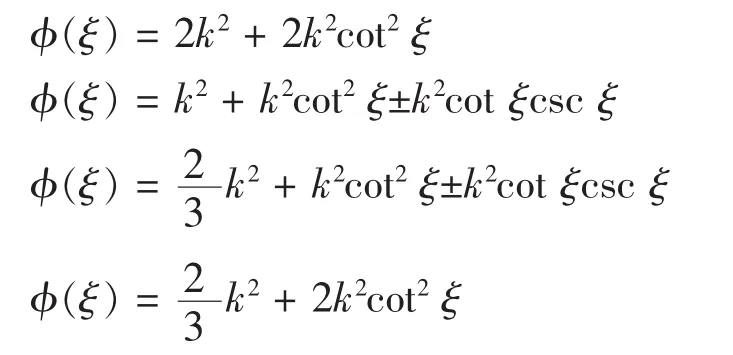
进一步由(2)式可得方程(1)的解为:
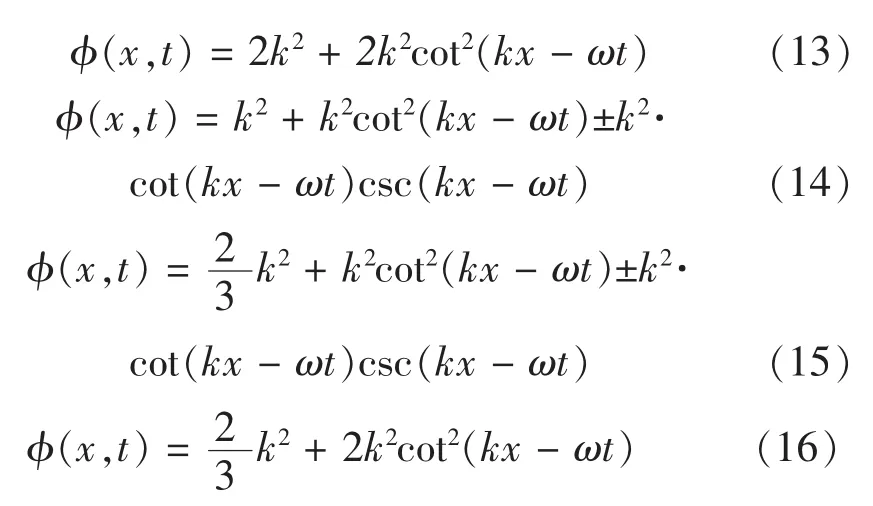
方法2:
设方程(4)有如下形式的行波解

如令

将(17),(18)代入(4)式,并令其中的常数项以及各次项的系数为零,得到如下线性方程组:

利用吴消元法解上述关于 A0,A1,A2,B1,B2的超待定代数方程组得:

对(18)式分离变量并且两边积分,积分常数取为零得:
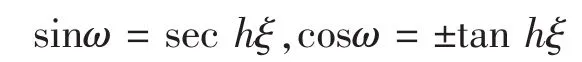
于是方程(4)有如下形式解
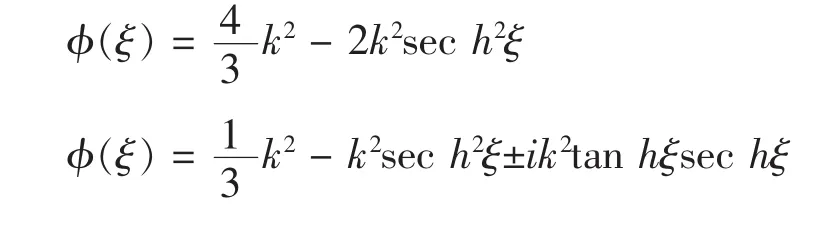
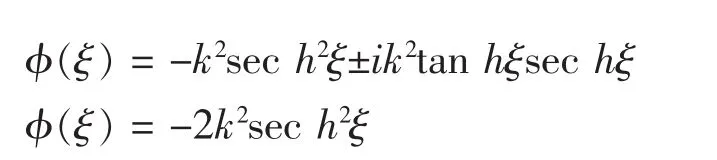
进一步由(2)式可得方程(1)的解为
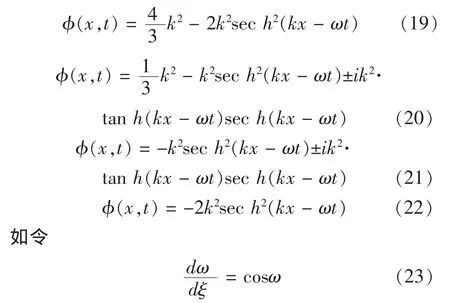
将(17),(23)代入(4)式,并令其中的常数项以及各次项的系数为零,得到如下线性方程组:

利用吴消元法解上述关于 A0,A1,A2,B1,B2的超待定代数方程组得:

对(23)式分离变量并且两边积分,积分常数取为零得:
于是方程(4)式得到如下解
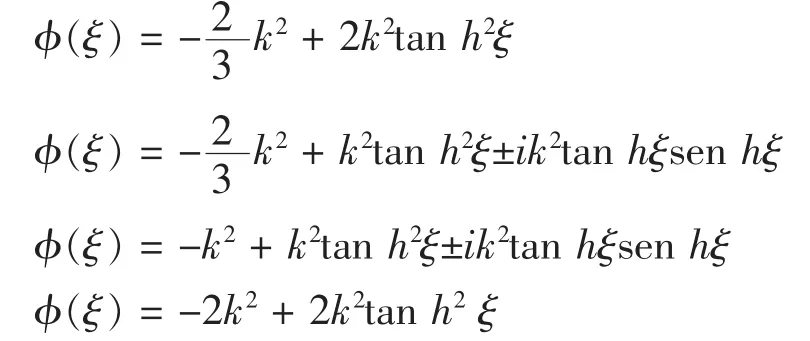
进一步由(2)式可得方程(1)的解为
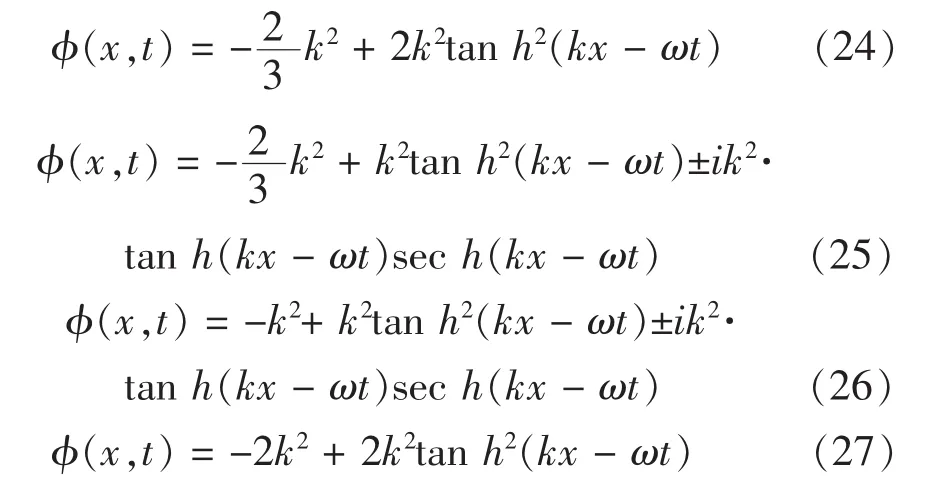

方法3:
又由双函数法设方程(8)有如下形式的行波解
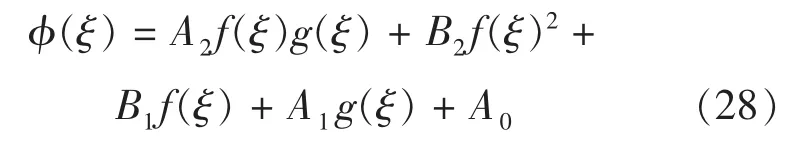
若取 f(ξ)和 g(ξ)为修正的双函数如下:
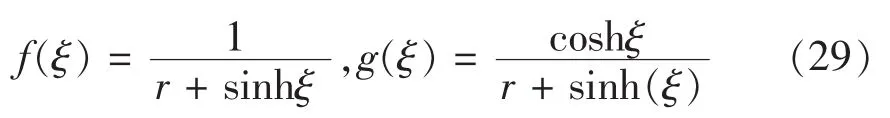
其中ξ为行波变量,r为参数,可以调整波行的变化.则易知:
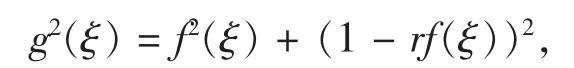
又易知:
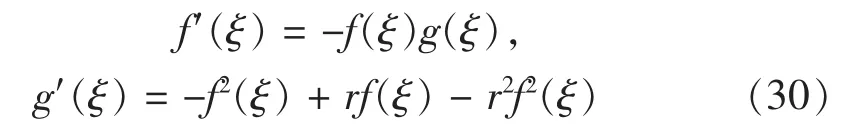
将(28)、(30)代入(4)中,并令其中的常数以及各次项的系数为零,得到如下线性代数方程组:
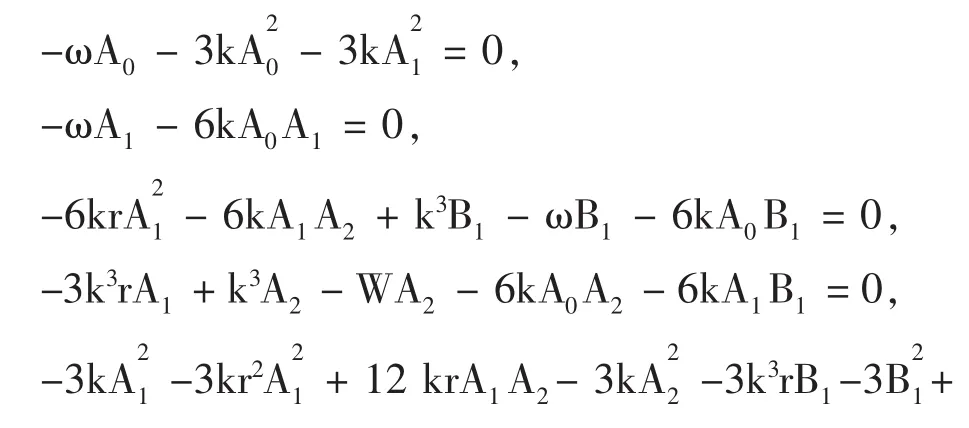

利用吴消元法解上述关于 A0,A1,A2,B1,B2的超待定代数方程组得(舍去和前面计算相同的答案):
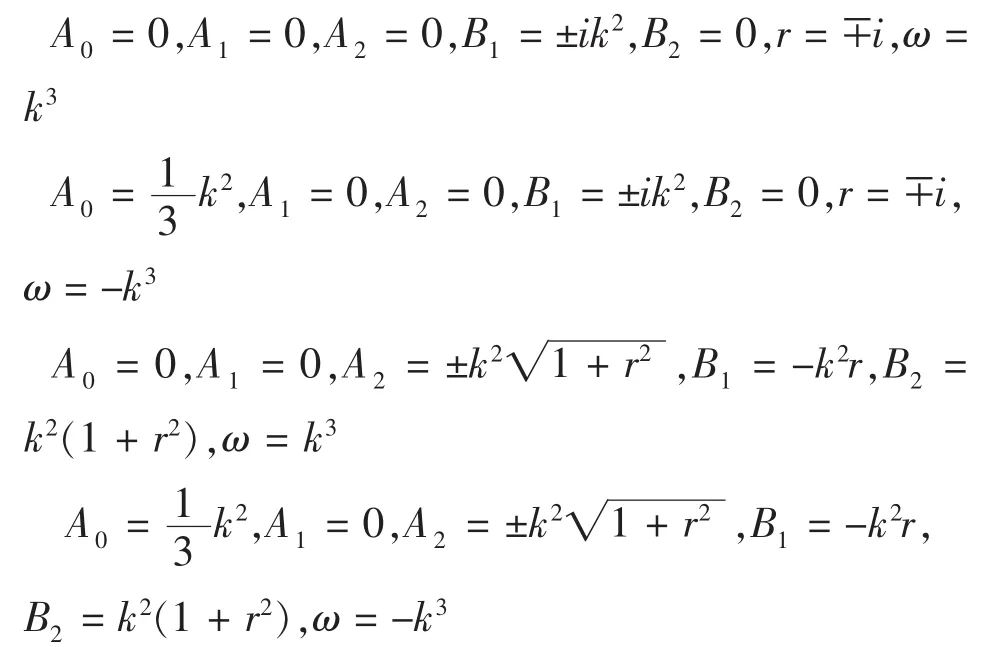
将以上结果及(29)式代入(28)式得
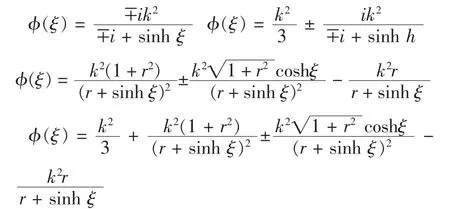
进一步由(2)式可得方程(1)的解为:
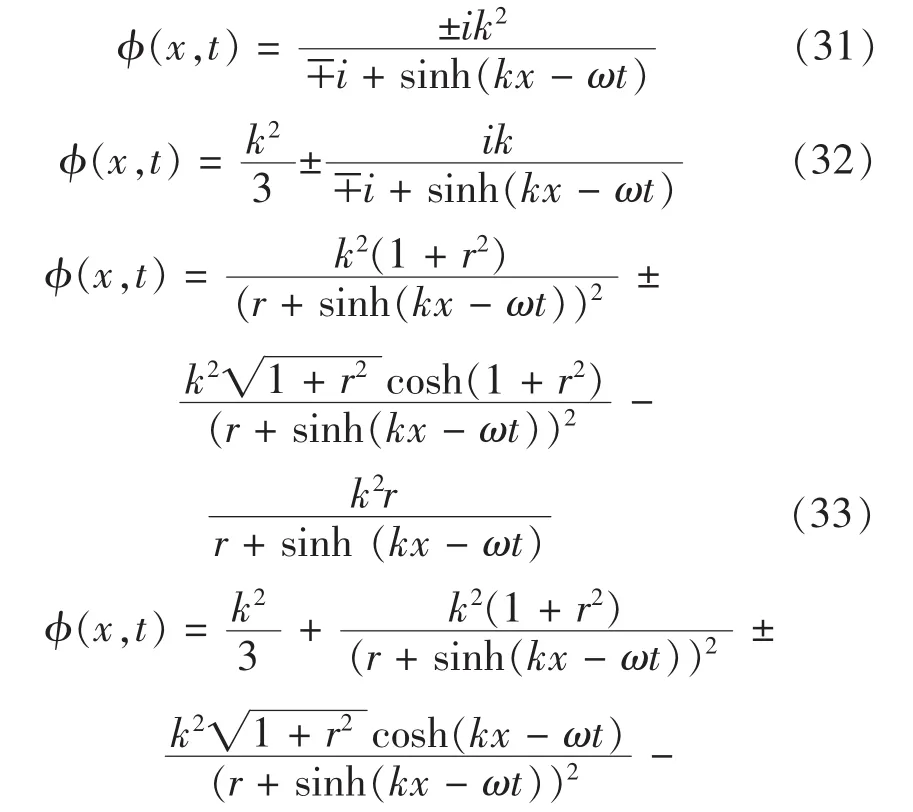
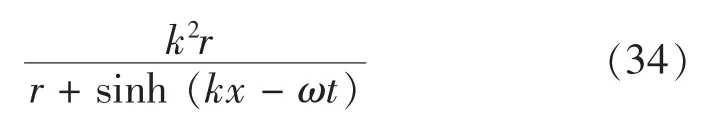
期中(31)、(32)为复标量场中的解

2 结语
本文采用双函数法和吴消元法,获得了kdv方程的多组孤波解,其中一些为复标量场中的解,丰富了kdv方程解的结果,将有助于我们对kdv方程所描述物理现象的进一步了解和研究.双函数法不仅可以用于求解一元非线性可积方程,而且可以用来求解非线性方程的各种解.其中双函数可以选择双曲函数,也可以选择三角函数等.
[1]Wang M L.Solitary Wave Solutionfor Varian Boussinesq equations[J].Phys Lett,1995,A199:169-172.
[2]Fan E G.Extended tanh-function method and its applications to nonlinear equations[J].Phys Lett,2000,A277:212-218.
[3]Kudryashow N A.Exact Solutions of the generalized Kuramoto-Sivashinsky equation[J].Phys Lett,1990,A147:287.
[4]Lin R L,Zeng Y B,Ma W Y.Solving the KdV Hierarchy with Self-Consistent Sources by Inverse Scatterin Method[J].Physica A,2001,291:287-298.
[5]Zeng Y B,Lin R L,Cao X.The Relation Between the Toda Hierarchy and the KdV Hierarchy[J].Phys Lett A,1998,251(3):177-183.
[6]韩家骅,陈良.关于一类非线性波动方程的准确周期解[J].安徽大学学报:自然科学版,2003,27(3):45-49.
[7]谢元喜,唐驾时.求一类非线性偏微分方程解析解的一种简洁方法[J].物理学报,2004,53(9):2828-2830.
[8]黎益,黎薰.解KdV方程的一个隐式差分格式[J].四川大学学报:自然科学版,1995,32(6):632-634.
[9]石玉仁,段文山,洪学仁,等.组合 KdV方程的显示精确解[J].物理学报,2003,52(2):267-270.
[10]赵长海,盛正卯.Zakharov方程的显式行波解[J].物理学报,2004,53(6):1629-1634.
[11]赵长海.非线性NLS方程的新显式精确行波解[J].南通大学学报:自然科学版,2007,6(3):12-15.
[12]关霭云.吴消元法讲义[M].北京:北京理工大学出版社,1994.
责任编辑:毕和平
Explicit Traveling Wave Solutions to kdv Nonlinear Equations
ZHAO ChangHai
(School of Science,Nantong University,Nantong 226007,China)
In this paper,multiple traveling wave solutions to kdv equation,including solition solutions and periodic solutions,were obtained by using hyperbola function method and Wu-elimination method.The method used in this work also can be applied to other nonlinear equations.
hyperbola function method;Wu-elimination method;kdv equation;traveling wave solution
O 415
A
1674-4942(2010)02-0142-05
2010-03-07
南通大学自然科学基金项目(06Z004)
