重温经典 回味无穷

●竺孟辉 (实验中学 浙江奉化 315500) ●应立君 (实验学校 浙江余姚 315400)

好的试题犹如一篇经典作品，时尝时新.不久前，在准备数学竞赛的练习题时，有一道几何证明题引起了师生的共同兴趣.

题目如图1，分别以锐角△ABC的3条边AB，BC，CA为斜边向外作3个等腰直角三角形△DAB，△EBC，△FAC.求证：

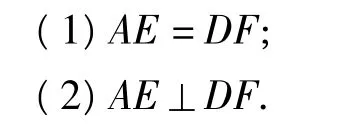
(2005年全国初中数学竞赛B卷试题)

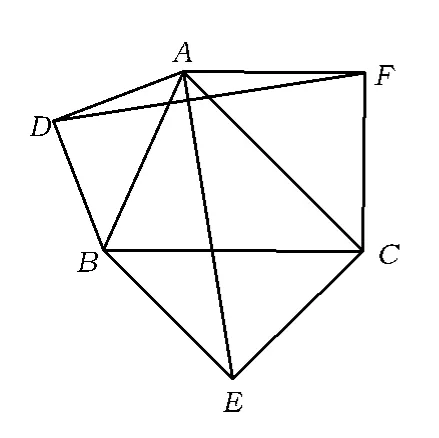
图1

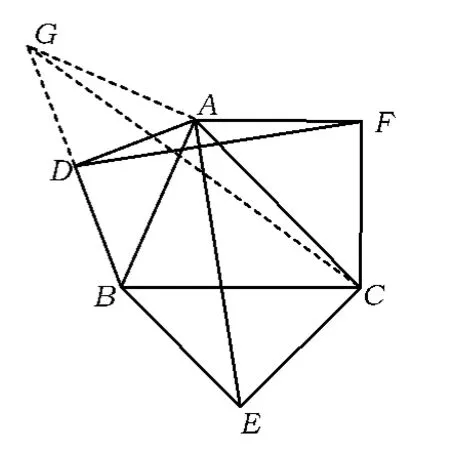
图2

方法1 向外补作一个等腰直角三角形，从中寻觅出几对相似三角形，推证出结论.

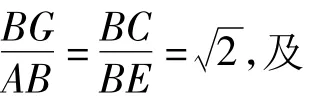
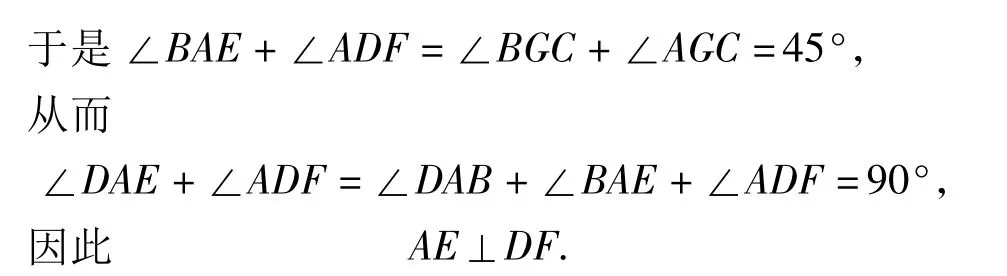
方法2 向内补作一个等腰直角三角形，得一正方形(思路来源于拿破仑三角形的证明).在此构图中寻觅相似形，推得结论.

证明(1)如图3，过点A，B分别作AG∥DB，BG∥AD，AG，BG 交于点 G，连结 GE，GF，易证四边形ADBG是正方形.由

图3

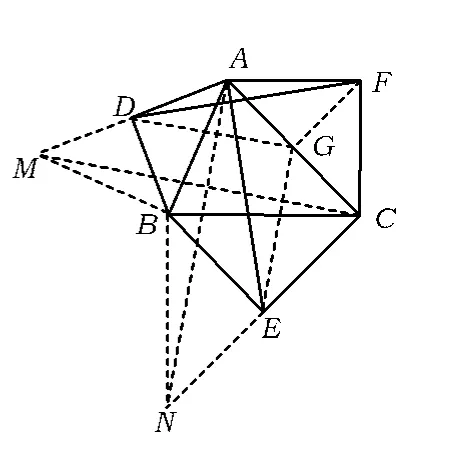
图4

方法3 取AC的中点G，延长AD至点M，使得DM=AD，延长 CE至点 N，使得 EN=CE，连结DG，EG，FG，MC，AN.通过证明△DFG≌△EAG，导出结论.

证明(1)如图4，取AC的中点G，延长AD至点M，使DM=AD，延长CE 至点N，使 EN=CE，连结 DG，EG，FG.MB，MC，NB，NA.易得△ABM，△CBN均为等腰直角三角形，则

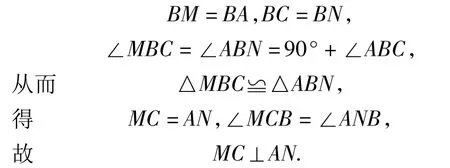
根据三角形中位线定理可得

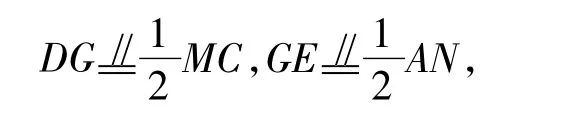
于是 DG=GE 且∠DGE=90°，从而△DFG≌△EAG，所以 DF=AE.

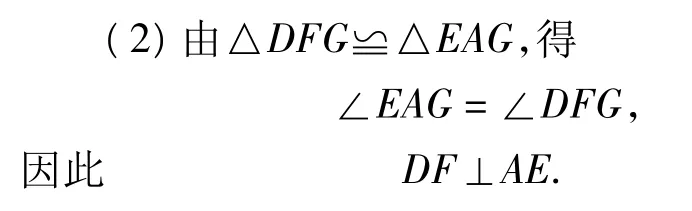
方法4 把△ADF绕点D顺时针方向旋转90°到△BDG，可证明四边形ADGE是平行四边形.

证明如图5，过点D作DG⊥DF，截取DG=DF，连结 GB，GE.易证△ADF≌△BDG，得

得AD∥GE，因此四边形ADGE是平行四边形，从而AE∥DG，且 AE=DG，于是

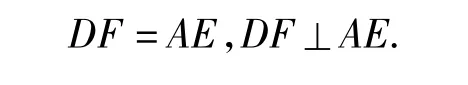
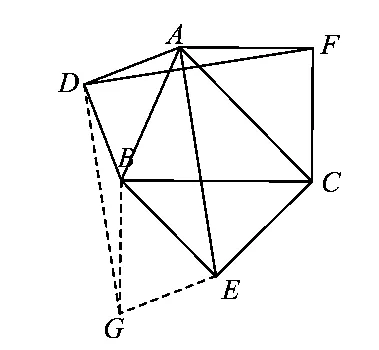
图5

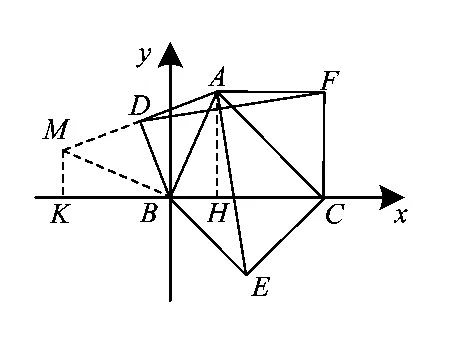
图6

方法5 建立平面直角坐标系，运用解析法，通过计算证明结论.

证明(1)如图6，以点B为坐标原点，BC所在直线为x轴，建立平面直角坐标系.设点A(a，b)，C(c，0)，延长 AD 至点 M 使得 DM=AD，连结BM.作AH⊥x轴交x轴于点H，MK⊥x轴交x轴于点 K.易证△MKB≌△BHA，得

(2)设直线DF的斜率为k1，直线AE的斜率为 k2，则

本例的解法既汇集了证明线段相等的多种基本方法，更是全等三角形、相似三角形、特殊四边形、三角形中位线、平行、垂直等知识与相关方法的一次综合运用.运用解析法(方法5)求证线段相等与垂直，对初中生来说，更是一次全新的尝试.