简论与圆有关的竞赛题

●章国水 王一杰 (元培中学 浙江绍兴 312000)

与圆有关的问题具有“知识上的综合性、题型上的新颖性、方法上的灵活性、思维的抽象性”等特点，因此圆的知识是初中数学中的重要内容之一，也是数学竞赛中的重要内容之一.本文结合实例对与圆有关的问题作一些剖析，以便能从中领略到该类问题的一般处理方式和策略.

1 与圆有关的计算题

圆既是轴对称图形，又是中心对称图形，它具有旋转对称性，这是圆的最重要的性质;弧、弦和直径的关系(垂径定理)，圆心角、圆周角、弦切角以及它们的大小与它们所对(或夹)的弧的度数之间的关系，则是圆中最基本的关系.它们都是研究有关圆的问题的基础，充分体现了圆的特色.这是解决与圆有关的问题的重要的基本知识，是证明与圆有关的结论的常用工具.

这一类计算题通常计算的是长度、角度、面积、比值、最值等，虽然计算的对象各有所别，但应用到的基础知识与方法同样具有圆问题的思维特色.

例1 如图1，已知四边形ABCD内接于直径为3的圆O，对角线AC是直径，对角线AC和BD的交点是 P，AB=BD，且PC=0.6，求四边形 ABCD的周长.

(1999年全国初中数学竞赛试题)

解设圆心为O，连结BO并延长交AD于点H.由AB=BD，点O是圆心，可得

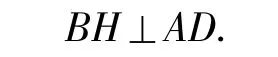
又由∠ADC=90°，得

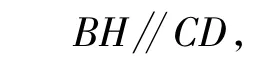
从而△OPB∽△CPD，于是

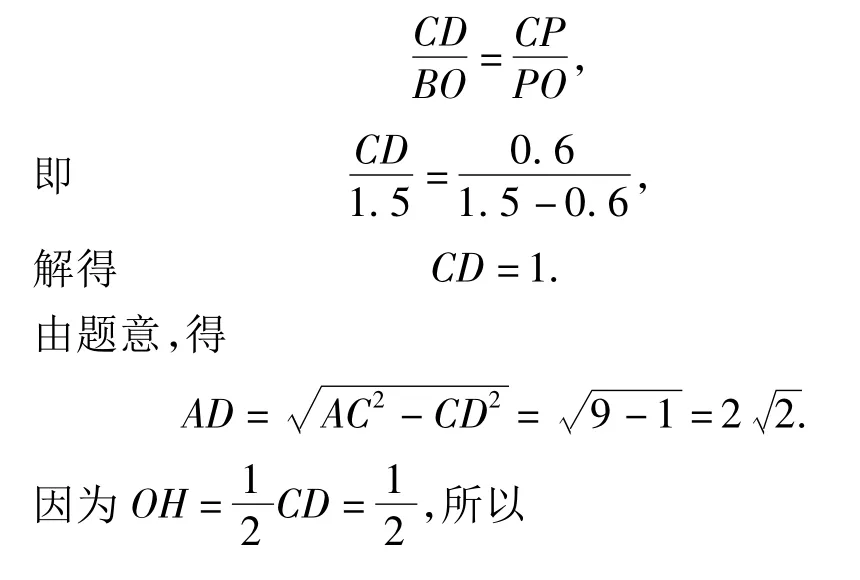
评注适当添加辅助线(连结BO并延长交AD于点H)，使条件与结论之间获得沟通，这正体现了本文所指的圆的特色.

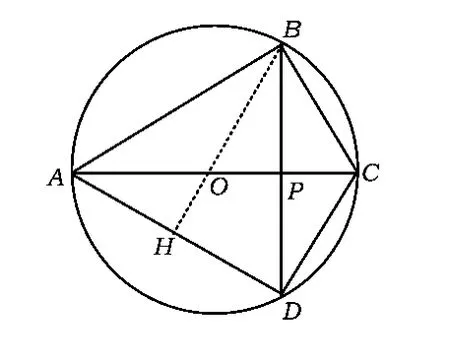
图1

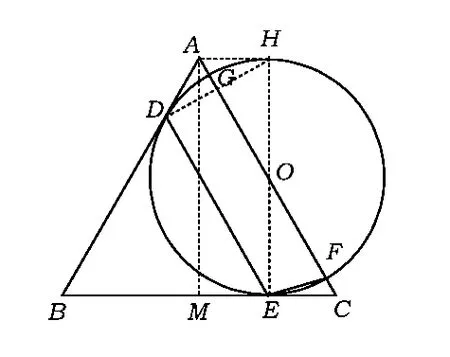
图2

例2 如图2，已知直径与等边三角形ABC的高相等的圆与边AB和BC相切于点D和E，与边AC相交于点F和G，求∠DEF的度数.

(2007年全国数学竞赛(浙江赛区)初赛试题)

解过点E作BC的垂线与圆交于点H，与AC交于点O，连结AH和DH，作AM⊥BC，垂足为M.因为E是切点，所以EH必过圆心，即EH是直径，从而DH⊥DE.又因为D，E是切点，所以BD=BE.由∠B=60°，得△DBE是正三角形，因此

由已知得AM=EH，又AM∥EH，所以四边形AMEH是矩形，因而 AH⊥HE，即AH是切线，从而 AD=AH，于是AC垂直平分DH，因此AC必过圆心，所以AC与EH的交点O是圆心，即

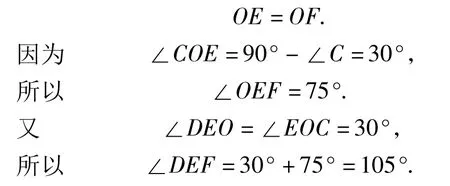
评注处理有关圆的切线的几何问题的基本思路是：由位置关系确定角的数量关系;反过来，又由数量关系确定直线与圆的位置关系.在解决这类问题的过程中，常常需借助图形中的直角三角形来解决.

(2000年全国初中数学竞赛试题)

解由题设得

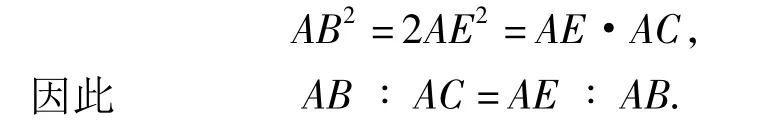
又由∠EAB=∠BAC，可得

连结AO，交BD于点H，则

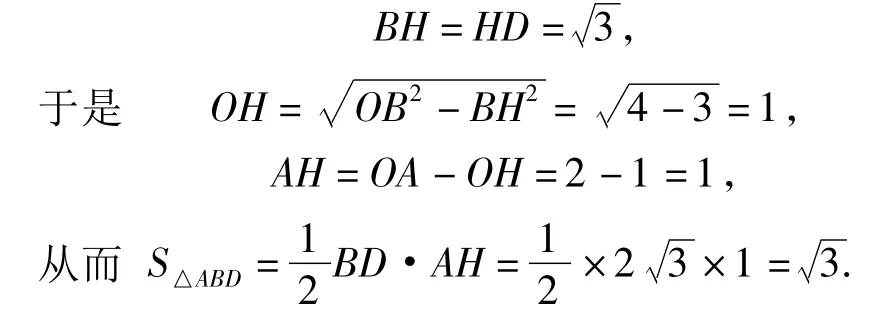
因为点E是AC的中点，所以

评注此例中有关元素的位置比较分散，通过添加辅助线(连结AO)把分散元素集中到某一个图形中，使彼此之间发生能体现圆的特色的关联.

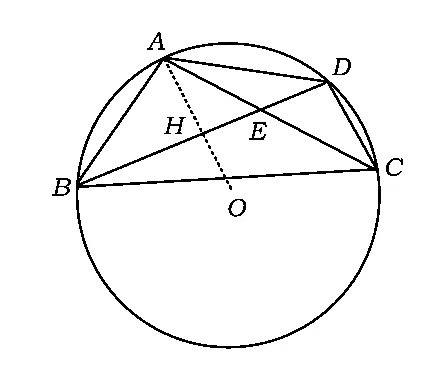
图3

图4

例4 如图4，圆O与圆D相交于点A，B，BC为圆D的切线，点C在圆O上，且AB=BC.

(1)证明：点O在圆D的圆周上;

(2)设△ABC的面积为S，求圆D的半径r的最小值.

(2008年全国初中数学联赛试题)

(1)证明 连结 OA，OB，OC，AC.因为 O 为圆心，AB=BC，所以△OBA∽△OBC，从而∠OBA=∠OBC.因为

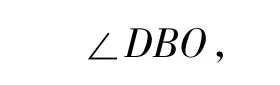
因此DB=DO，故点O在圆D的圆周上.

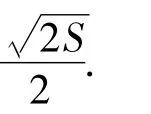
评注在圆的问题中常能找到直角与一些相等的角，这就使这样的问题常常能利用勾股定理与相似三角形的知识来解决.

2 与圆有关的证明题

证明线段相等、角相等、线的位置关系(平行、垂直)的这类问题主要考查全等三角形和相似三角形的判定，垂径定理及其推论，圆周角、圆心角的性质，及切线的性质，弦切角等有关圆的基础知识.

证明等积式、等比式及混合等式等的这类问题主要考查相似三角形、切割线定理及其推论、相交

其中当a=y时等号成立.这时，AC是圆O的直径，故圆D的半径r的最小值为弦定理及圆的一些知识.

例5 已知在△ABC中，∠ACB=90°，边 AB 上的高线CH与△ABC的2条内角平分线AM，BN分别交于点 P，Q，PM，QN 的中点分别为E，F(如图5).求证：EF∥AB.

(2009年全国初中数学联赛试题)

证明由BN是∠ABC的平分线，得∠ABN=∠CBN.又由CH⊥AB，可得

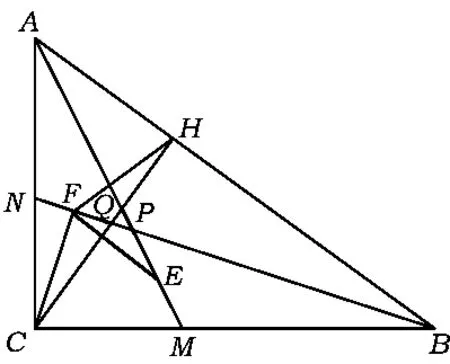
图5

又F是QN的中点，得CF⊥QN，因此

于是点 C，F，H，B 共圆.从而∠FBH=∠FBC，所以FC=FH，故点F在CH的中垂线上.同理可得，点E在CH的中垂线上.因此EF⊥CH.又AB⊥CH，所以EF∥AB.

例6 已知在等腰△ABC中，如图6，AB=AC，∠C的平分线与边AB交于点P，M为△ABC的内切圆⊙I与边BC的切点，作MD∥AC，交⊙I于点D.证明：PD是⊙I的切线.

(2010年全国初中数学联赛试题)

证明过点P作⊙I的切线PQ(切点为Q)并延长，交BC于点N.因为CP为∠ACB的平分线，所以∠ACP=∠BCP.又因为PA，PQ均为⊙I的切线，所以∠APC=∠NPC.由 CP公共，得△ACP≌△NCP，因此∠PAC=∠PNC.又由 NM=QN，BA=BC，得△QNM∽△BAC，于是∠NMQ=∠ACB，从而MQ∥AC.又因为MD∥AC，所以MD和MQ在同一条直线上.又点Q，D均在⊙I上，所以点Q和点D重合，故PD是⊙I的切线.

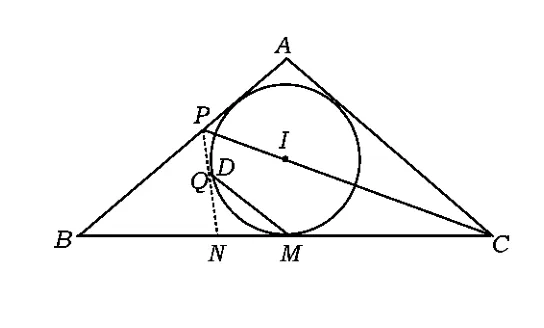
图6

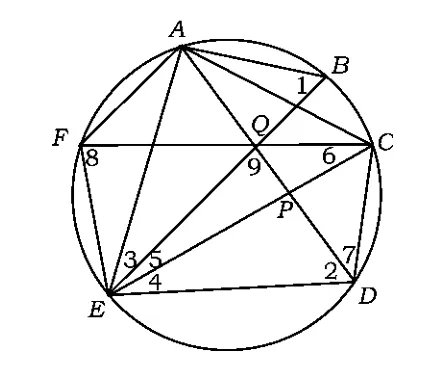
图7

例7 如图7所示，圆内接六边形ABCDEF满足AB=CD=EF，且对角线 AD，BE，CF交于一点Q，设AD与CE的交点为P.

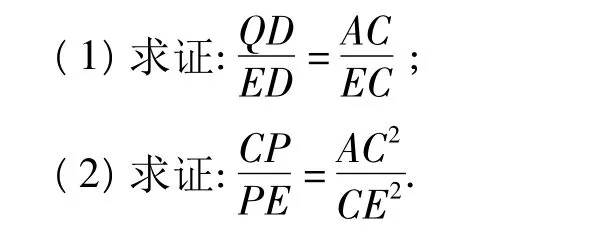
(2002年全国初中数学竞赛试题)

分析(1)易证∠3=∠4，因此∠AEC=∠DEQ.而∠ACE=∠2，于是△ACE∽△QDE，可得结论成立.

这只需证△CQD∽△EQD.而由题设有

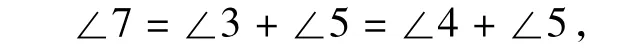
由第(1)小题得∠9=∠EAC，而

故可证得△CQD∽△EQD.

评注证明乘积式相等，一般可把乘积式转化为比例式，再看比例式中的4条线段能否作为某相似三角形的对应边.

例8 已知：如图8，在以AB为弦的弓形劣弧上取一点M(不包括点A，B)，以M为圆心作圆M和AB相切，分别过点A，B作⊙M的切线，2条切线相交于点C.求证：∠ACB有定值.

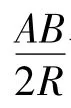
证明在△ABC中，∠MAB+∠MBA=180°-∠AMB.由M是△ABC的内心，得

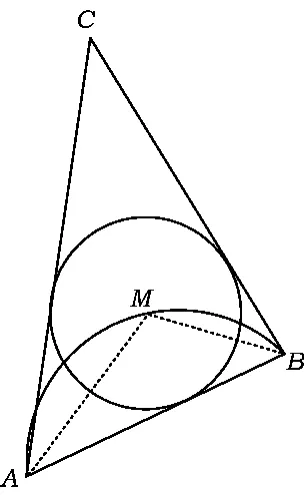
图8

评注几何定值问题一般都要通过特殊位置的计算，先找到这个定值.而本例的定值，显然是与∠AMB有关的.