简述几何不等式、几何最值与几何变换的问题

●毛幼娥 (柯岩中学 浙江绍兴 312030)

平面图形中的几何量包含线段长度、角的大小及图形的面积.每类几何量之间除了有相等关系之外，多数情况下呈现的是不等关系.研究这些不等关系就构成了几何不等式的内容.一种图形中的几何量若在某约束条件下它的值在一定范围内变化，人们很自然地会提出什么时候这个量最大(或最小)的问题，这类问题与几何不等式有着密切的联系，被称为几何最值问题.本文就初中数学知识范围内讨论上述问题.

1 几何不等式与几何变换

几何不等式主要有线段不等式、角的不等式以及面积不等式.以下是几个经常被用到的定理.

定理1 (三角形不等式)若A，B，C为任意3个点，则AB≤AC+CB.当且仅当点C位于线段AB上时，等号成立.

定理2 在三角形中，大角(边)对大边(角).

定理3 在2对边对应相等的2个三角形中，夹角(第3边)大的第3边(夹角)大.

定理4 三角形一边上的中线小于另两边和的一半.

定理5 由定直线l外一点P到直线l上的点的连接线段之长，以点P到定直线l的垂线段的距离为最短.

证明几何不等式，需要添作辅助线，常与几何变换密切相关.

例1 在△ABC中，∠B=2∠C，求证：AC ＜2AB.

证明如图1所示，延长CB到点D，使BD=AB.连结AD，则在△ABC中，∠ADB=∠DAB，因此

图1

于是∠C=∠D，故AC=AD.在△ABD中，

但AB=BD，于是

说明 通过几何图形的变换——可看作是一种旋转变换，把线段BA绕着点B转过∠ABC的补角，把要比较的线段与角相对集中.借助几何变换证明几何不等式，是一条重要的解题思路.

推广题在△ABC中，∠ABC=n∠BCA(n为大于1的自然数)，则AC＜nAB.

变式题如图2，在△ABC中，AB=AC，P是△ABC内一点，∠APB＞∠APC，求证：PB＜PC.

例2 在2条对角线长度及夹角一定的所有凸四边形中，试求周长最小的四边形.

图2

分析如图 3，取 AC，BD的中点E，F，连结EF.将AC沿EF方向平移到A'C'，连结A'B，BC'，C'D，DA'，则 A'BC'D 是一个符合条件的平行四边形.延长AF，CC'交于点 G.由点 E是AC 的中点，且 EF∥CC'，FC'∥EC，可得 F，C'分别为 AG，CG 的中点，因此

图3

同理可得

相加得

故当四边形为长度一定的对角线夹角为己知定角的平行四边形时，周长最小.

说明 辅助线虽多，但站在几何图形变换的角度，就很清楚了.

例3 如图 4，已知∠MON=20°，点 A为 OM 上一点，OA=4 3，D为ON上一点，OD=8，C为射线AM上任意一点，B是线段OD上任意一点.求证：折线 ABCD的长AB+BC+CD≥12.

证明以OM为轴，作点D关于OM的对称点D1，连结 OD1，则∠MOD1=20°.又作点 A 关于 ON的对称点 A1，连结 OA1，则∠A1ON=20°，因此∠A1OD1=60°.连结 A1D1，A1B，CD1，则

图4

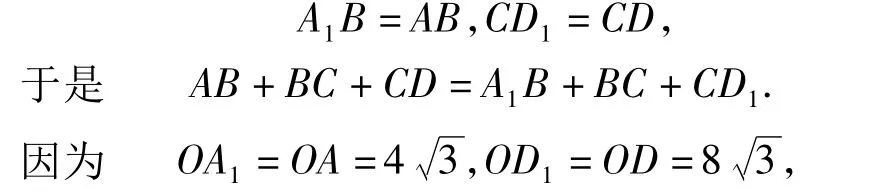
所以A1，D1为定点，因此连结定点A1，D1间的折线以线段A1D1为最短，从而

可以用同一法证明△A1OD1是直角三角形，因此

说明 本题是通过另一种几何变换——轴对称变换把折线“化直”，利用两定点间线段最短来证明的.需要注意的是：通过轴对称变换后，折线与线段比较时，折线与线段的2个公共端点必须是定点，这样才能确定这线段之长是个定值.

变式题设∠MON=20°，A为 OM上一点，OA=4;D为ON上一点，OD=8.试在AM上找一点C，在OD上找一点B，使得AB+BC+CD的长度最小.请确定点B，C的位置，并求出AB+BC+CD的长度的最小值.

虽然问题形式改变了，但实质内容是一样的.可见，不等式问题与极值问题有着紧密的联系.

例4 求证：任意三角形的3个内角平分线的乘积必小于3条边的乘积.

证明设 a，b，c为△ABC的3 条边，ta，tb，tc为△ABC 的 3 个内角的平分线.如图5，作△ABC的外接圆与∠A的平分线AD的延长线相交于点E，则

图5

3式相乘得

说明 本题可看作由圆生成的一些等角得来的相似变换解题.

2 几何极值问题与几何不等式

例5 已知A，B两村在河流MN的同侧，现需在河流MN边建一抽水站，同时为A，B两村供应自来水，请问抽水站应建在什么地方，使得到A，B两村的水管最短.

分析本例的求解也是借助于轴对称变换!

如图6，要使A，B两村的水管最短，关键是要在MN上找到点P，使得AP+BP有最小值，直接找点 P显然有困难，因此需要对这个问题进行转换.由“连结对称点的线段被对称轴垂直平分”和“线段垂直平分线上任意一点到线段两端点距离相等”可知，点B和它关于河流MN的对称点B'到抽水站点P的距离相等，因此讨论AP+BP的最小值问题转化为求AP+B'P的最小值问题.显然，A，B'之间线段最短，于是连结AB'，与MN相交于点P，点P就是建抽水站点.

图6

变式题如图7，正方形的边长为8，点M在DC上，且DM=2，N是 AC上的一动点，则DN+MN 的最小值为_______(也要借助于轴对称变换来添线引路).

图7

图8

例6 设A，B两镇分别在河R的两岸，假定河R各处的宽度是相等的，现在想在河上垂直于河岸建一座桥.问桥应该修在什么地方，才能使从A镇经过桥到B镇的总路程最短?

分析本例是借助平移变换来解决问题的.

由于河R的宽度一定，桥又垂直于河岸，因此可设桥长为定值d.假设河岸为2条平行直线m，n，设桥架在CD处，则要使BC+CD+DA最短，只需BC+DA最短.假想点B和直线m所在的半平面向下平移距离d，这时直线m与n重合，点C与点D重合，点B到了点B1的位置，于是只需B1D+DA最小即可.但两点之间以线段最短，所以点D应是AB1与直线n的交点，于是桥的位置即可作出了.

作法 如图8，把点B向下平移距离d到点B1，连结AB1，交直线n于点D.过点D作直线n的垂线交直线m于点C，连结BC，则CD即为桥的位置，且使得BC+CD+DA最短.

证明设在另外的地点垂直于河岸架桥C1D1，连结 BC1，B1D1，D1A，则 BB1∥C1D1，因此BB1D1C1为平行四边形，于是BC1=B1D1.由B1D1+D1A ＞B1A，得

因此桥CD的确为所求(使BC+CD+DA最短)的位置.

说明 一般地，若要求证的不等式以“≤”或“≥”的形式出现，则寻求等号成立的几何条件就会得到相应的几何极值.

例7 在凸四边形ABCD中，AB+AC+CD=16(如图9)，问：当对角线AC，BD为何值时，四边形ABCD面积最大?最大值是多少?

(第九届华杯赛总决赛笔试初二组一试试题)

解设 AB=x，AC=y，则

图9

当且仅当∠BAC=∠ACD=90°及y=8时，两处都取到等号.故当y=8 时，S四边形ABCD的最大面积为32.

当 S四边形ABCD取到最大面积时，凸四边形 ABCD如图10所示.由∠BAC= ∠ACD=90°，AC=8，根据勾股定理得BD=8.

图10

例8 在△ABC中，最大角小于120°.试在△ABC内取一点P，使得点P到3个顶点距离之和PA+PB+PC为最小.

解设P为△ABC内任一点，把△ABP绕点B作逆时针方向旋转60°，点P转到点P'，点A转到点A'(如图11).因为

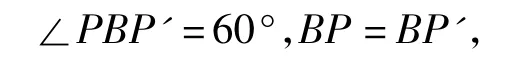
所以△BPP'是正三角形，于是

又因为A'，C都是定点，所以A'C是PA+PB+PC的最小值.当且仅当点 C，P，P'，A'共线时，取到等号.而在点 C，P，P'，A'共线时，

因此点P是以BC为弦、含120°角的位于三角形ABC内的弓形弧与以AB为弦、含120°角的位于三角形ABC内的弓形弧的交点.这个点就是著名的费马点.

反过来，若点P是费马点，则

因此点 C，P，P'共线.同理可得

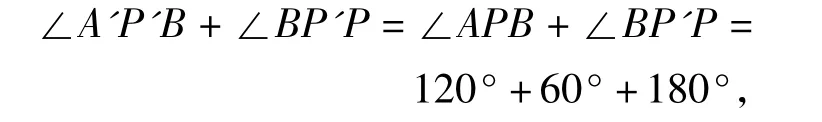
于是点 A，P'，P 共线，因此点 A'，P'，P，C 共线.故点P一定是PA+PB+PC取得最小值的点.

说明 本例借助旋转变换，把汇聚于一点的3条线段PA，PB，PC，转化为1条折线CPP'A'!

图11 图12

变式如图12，已知点O是△ABC内一点，∠AOB=∠BOC=∠COA=120°，P是△ABC内任一点，求证：PA+PB+PC≥OA+OB+OC.

［1］ 周春荔.数学创新意识培养与智力开发［M］.北京：首都师范大学出版社，2000.