解析几何中的定值问题

●蒋瑞龙 (杭州外国语学校 浙江杭州 310023)

解析几何中的定值问题是数学高考和竞赛中的热点问题.在“以能力立意”的指导思想下，定值问题综合性强，能够广泛地联系不同的数学知识和基本方法.这类题目立意新颖，能较好地考查学生对知识掌握的熟练性和灵活性.本文举例探讨定值问题的常见类型与求解策略，以供参考.

1 线段长度比为定值的问题

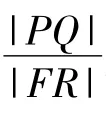
证明设 F(-c，0)，P(x1，y1)，Q(x2，y2)，直线PQ的方程为y=k(x+c).与椭圆方程联立后，消去y整理得

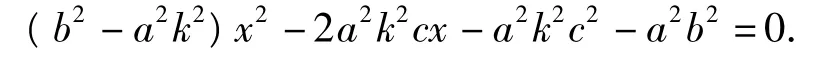
由韦达定理可得

从而弦PQ的中点为

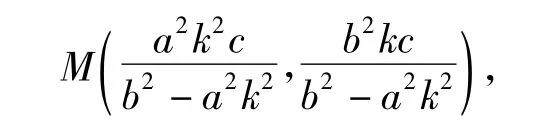
直线MR的方程为

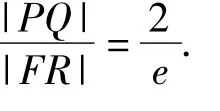
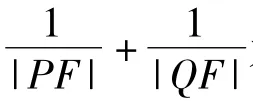
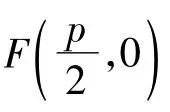
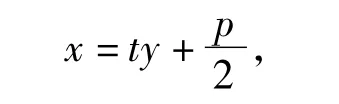
与抛物线方程联立后，消去x整理得

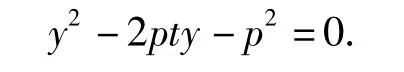
由韦达定理可得

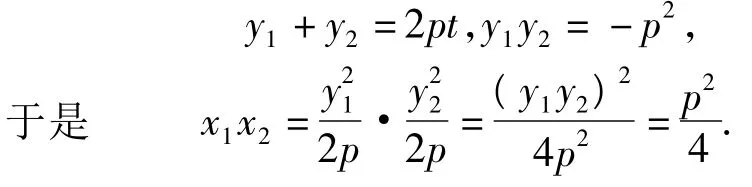
由抛物线定义得到的焦半径公式，可知

2 直线斜率或角度为定值的问题

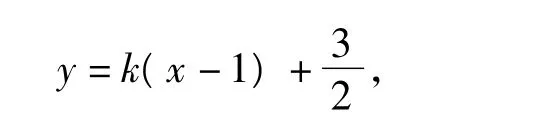
代入椭圆方程得

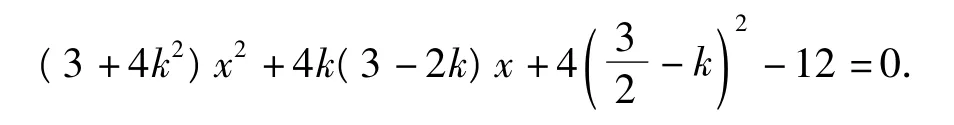
它有2个根1与xE，由韦达定理可得

又直线AF的斜率与AE的斜率互为相反数，在上式中以-k代k，可得

于是直线EF的斜率为

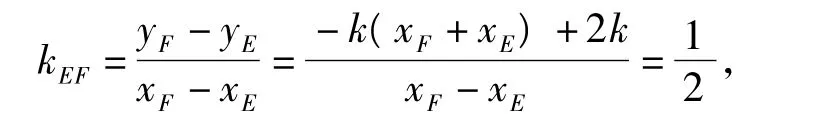
评析 本题若改为作与OA平行的直线交椭圆于点E，F，则有结论：AE，AF的斜率互为相反数.

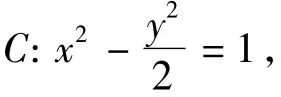
解点 P(x0，y0)(x0y0≠0)在圆 x2+y2=2上，圆在点P(x0，y0)处的切线方程为

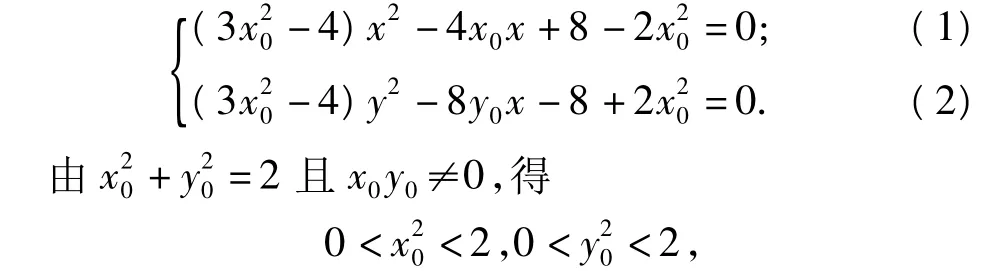
设点 A，B 的坐标分别为(x1，y1)，(x2，y2)，则

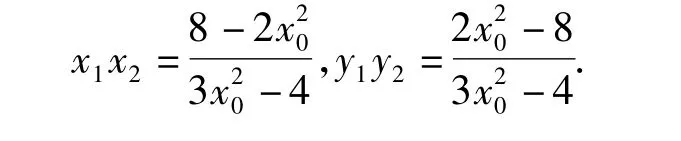
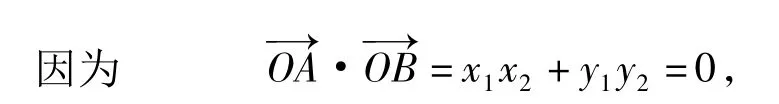
所以∠AOB的大小为定值90°.

3 动直线过定点问题

例5 已知点A(x0，y0)为抛物线y2=2px(p＞0)上的一定点，过点A作抛物线的2条弦AB，AC，证明：当AB⊥AC时，直线BC恒过一定点.

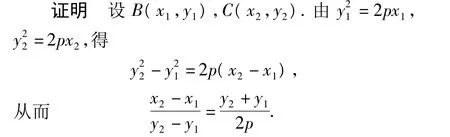
直线BC的方程为

由点 A(x0，y0)在抛物线上，即=2px0，得

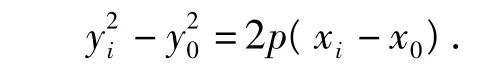
若 AB⊥AC，则

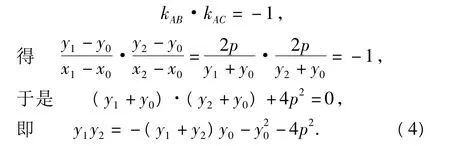
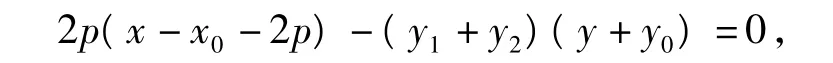
这就说明了直线BC恒过定点P(x0+2p，-y0).

逆命题即：“……直线BC过定点P(x0+2p，-y0)，则AB⊥AC”也是成立的，证明时只需把上面的过程稍作调整即可.

(2)本命题在椭圆和双曲线中有类似的结论.

例6 过抛物线x2=2py(p＞0)的准线l上一点M，作抛物线的2条切线，切点分别为A，B.证明：直线AB恒过焦点.

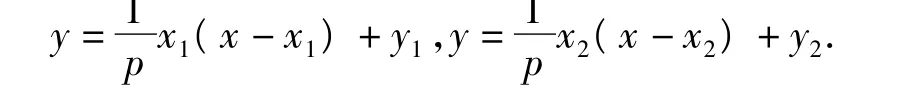
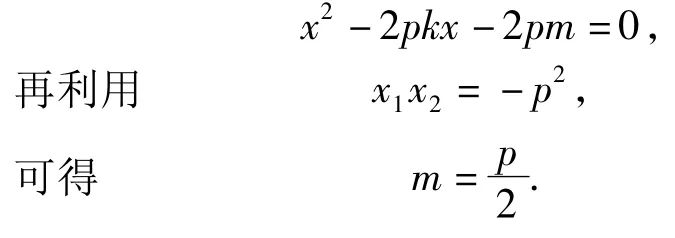
4 探求型问题

例7 已知抛物线C：y2=2px(p＞0)，在抛物线C外任取一点P(a，b)，求证：在抛物线上必存在一点Q，使得过点P作的抛物线的任意一条弦MN，都有kOM·kQN为常数.

令kQM·kQN=r为常数，则设直线MN的方程为由 y1，y2是方程(6)的2个根，得

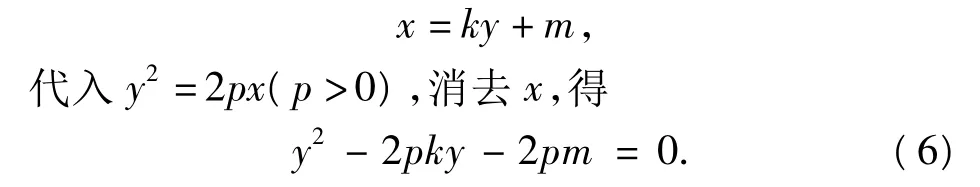
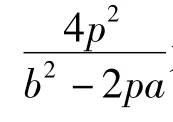
评析 本题变换角度从反面进行思考，在抛物线上过点Q任作2条弦，然后假定kQM·kQN=r为常数，找到直线过定点，从而使问题获解.这种反其道而行之的方法，是探索型问题中最为常用的方法之一.