抽屉原理在初中数学竞赛中的应用

●胡新颖 (东阳市外国语学校 浙江东阳 322100)

1 抽屉原理的含义

抽屉原理又称鸽巢原理，它的数学表述为：

原理1 把n+1个元素分成n类，不管怎么分，则一定有一类中有2个或2个以上的元素.

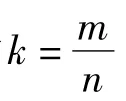
原理3 把无穷多个元素放入有限个集合里，则一定有一个集合里含有无穷多个元素.

抽屉原理也被称为迪里赫莱原理(因为最先是由德国数学家迪里赫莱明确提出来的)，它是组合数学的一个基本原理.

2 抽屉原理的应用

应用抽屉原理解题，一般可分为以下几个步骤：

第1步：分析题意.分清什么是“东西”，什么是“抽屉”.

第2步：构造抽屉.根据题目条件与结论，抓住基本的数量关系，确定抽屉的个数，并设计出解决问题所需的抽屉.这是解题的关键一步!

第3步：运用抽屉原理解决问题.

例1 (1)体育用品仓库里有许多足球、排球和篮球，某班50名同学来仓库拿球，规定每个人至少拿1个球，至多拿2个球，问至少有几名同学所拿的球的种类是一致的?

(2)某校有55个同学参加数学竞赛，已知将参赛人任意分成4组，则必有一组的女生多于2人;又知参赛者中任何10人中必有男生，则参赛的男生人数为多少人?

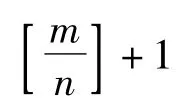
(2)因为任意分成4组，必有一组的女生多于2人，所以女生至少有4×2+1=9(人);又因为任意10个人中必有男生，所以女生人数至多有9人.故女生有9人，男生有55-9=46(人).

例2 从1～100的自然数中，任意取出51个数，证明：其中一定有2个数，它们中的一个是另一个的整数倍.

分析本题似乎茫无头绪，从何入手?其关键何在?其实就在“2个数”，其中一个是另一个的整数倍.巧妙地构造“抽屉”，使得每个抽屉里任取2个数，都有一个是另一个的整数倍.这里需要用到自然数分类的基本知识：任何一个正整数都可以表示成一个奇数与2的方幂的积，即若m∈N+，k∈N+，n∈N，则 m=(2k-1)·2n，并且这种表示方式是唯一的，如1=1 ×2°，2=1 ×21，3=3 ×2°，…

因为任何一个正整数都能表示成一个奇数乘2的方幂，并且这种表示方法是唯一的，所以可把1～100的正整数分成如下50个抽屉(因为1～100中共有50个奇数)：

这样，1～100的正整数就无重复、无遗漏地放进这50个抽屉内了.从这100个数中任取51个数，也即从这50个抽屉内任取51个数.根据抽屉原则，其中必定至少有2个数属于同一个抽屉，即属于(1)～(25)号中的某一个抽屉.显然，在这25个抽屉中的任何同一个抽屉内的2个数中，一个是另一个的整数倍.

说明 从上面的证明中可以看出，本题能够推广到一般情形：从1到2n的自然数中，任意取出n+1个数，则其中必有2个数，它们中的一个是另一个的整数倍.因为1到2n中共含1，3，…，2n-1这n个奇数，所以可以制造n个抽屉，而n+1＞n，由抽屉原则知，结论必然成立.

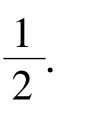
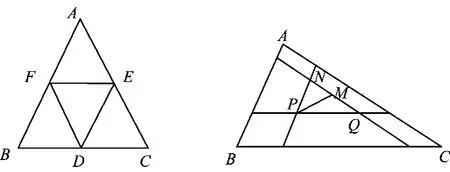
图1 图2

分析5个点的分布是任意的.如果要证明“在边长为1的等边三角形内(包括边界)有5个点，则这5个点中一定有距离不大于的2个点”，那么顺次连结三角形3条边的中点，即三角形的3条中位线，可以分原等边三角形为4个全等的边长为的小等边三角形，则5个点中必有2个点位于同一个小等边三角形中(包括边界)，其距离便不大于.

以上结论要由定理“三角形内(包括边界)任意2点间的距离不大于其最大边长”来保证，下面证明这个定理.

证明如图2，设BC是△ABC的最大边，P，M是△ABC内(包括边界)任意2个点，连结PM.过点P分别作边AB，BC的平行线，过点M作边AC的平行线.设各平行线的交点为P，Q，N，则

∠PQN=∠C，∠QNP=∠A.

因为BC≥AB，所以∠A≥∠C，则∠QNP≥∠PQN.而∠QMP≥∠QNP≥∠PQN(三角形的外角大于不相邻的内角)，于是 PQ≥PM.显然 BC≥PQ，故BC≥PM.由此可知，边长为的等边三角形内(包括边界)两点间的距离不大于.

说明 (1)这里是用等分三角形的方法来构造“抽屉”的.类似地，还可以利用等分线段、等分正方形的方法来构造“抽屉”.例如“任取n+1个正数 ai，满足 0 ＜ ai≤1(i=1，2，…，n+1)，试证明：这n+1个数中必存在2个数，其差的绝对值小于”.又如：“在边长为1的正方形内任意放置5个点，求证：其中必有2个点，这2个点之间的距离不大于

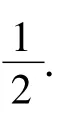
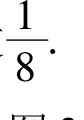
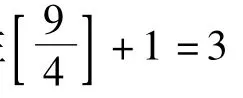
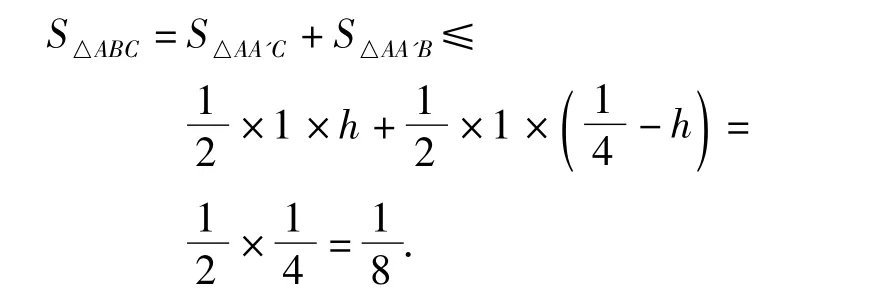
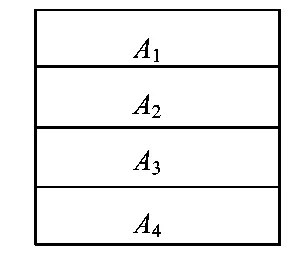
图3

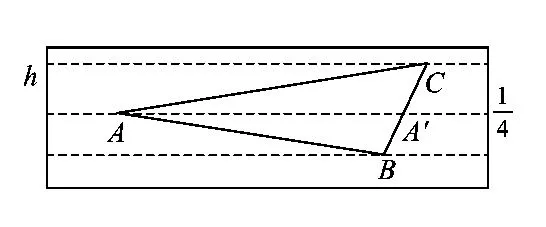
图4

说明 把正方形分成4个区域，可以得出“至少有1个区域内有3个点”的结论，这就为确定三角形面积的取值范围打下了基础.本题构造“抽屉”的办法不是唯一的，还可以将正方形等分成边长为的4个小正方形等(如图5).但是如将正方形等分成4个全等的小三角形却是不可行的(想一想为什么)，因此适当地构造“抽屉”，正是应用抽屉原则解决问题的关键所在.

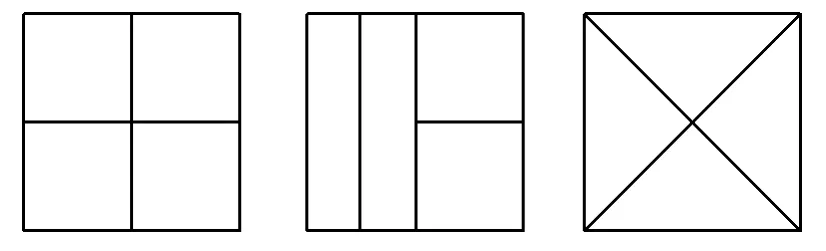
图5

例5 9条直线的每一条都把一个正方形分成2个梯形，而且它们的面积之比为2 ∶3.证明：这9条直线中至少有3条通过同一个点.

图6

分析设正方形为ABCD，点E，F分别是AB，CD的中点.设直线l把正方形ABCD分成2个梯形ABGH和 CDHG，并且与EF相交于点P(如图6)，其中梯形ABGH的面积∶梯形CDHG的面积 =2 ∶3，EP是梯形ABGH的中位线，PF是梯形CDHG的中位线.由于梯形的面积=中位线×梯形的高，并且2个梯形的高相等(AB=CD)，于是梯形ABGH的面积 ∶梯形CDHG的面积=EP ∶PF，也就是EP ∶PF=2∶3，这说明，直线l通过EF上一个固定的点P，这个点把EF分成长度为2∶3的2个部分.这样的点在EF上还有1个，如图6中的点Q(FQ ∶QE=2 ∶3).

同样地，如果直线l与AB，CD相交，并且把正方形分成2个梯形面积之比是2∶3，那么这条直线必定通过AD，BC中点连线上的2个类似的点(三等分点).这样，在正方形内就有4个固定的点，凡是把正方形面积分成2个面积为2∶3的梯形的直线，就一定通过这4个点中的某一个.把这4个点看作4个“抽屉”，9条直线看作9个“苹果”，由定理2可知因此必有一个抽屉内至少放有3个苹果，也就是必有3条直线要通过1个点.

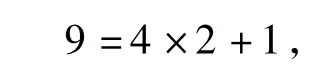
说明 本例中的抽屉比较隐蔽，正方形2双对边中点连线上的4个三等分点的发现是关键，而它的发现源于对梯形面积公式——S梯形 =中位线×梯形的高的充分感悟.