再谈调和四边形的性质及应用
2010-08-27沈文选湖南师范大学数学奥林匹克研究所湖南长沙410081
●沈文选 (湖南师范大学数学奥林匹克研究所 湖南长沙 410081)
笔者在文献[1]中介绍了调和四边形的7条性质及7道应用的例题.在此,再介绍调和四边形的一些有趣性质及应用的例子.
性质8 圆内接四边形为调和四边形的充要条件是该四边形4个顶点与不在其圆上一点的连线交圆于4点为一正方形4个顶点.
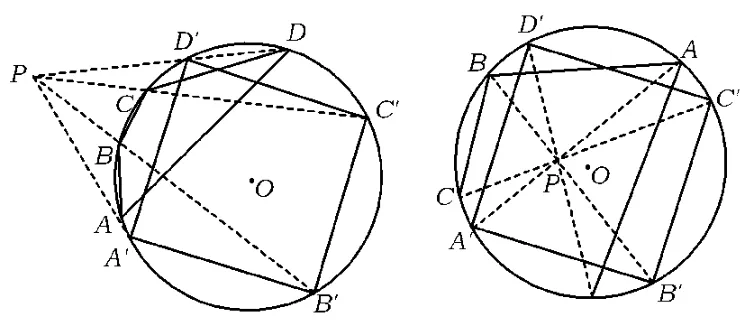
图1
证明如图1,四边形ABCD内接于⊙O,点P不在⊙O的圆周上,直线 PA,PB,PC,PD分别交⊙O 于点 A',B',C',D'.由割线或相交弦定理得

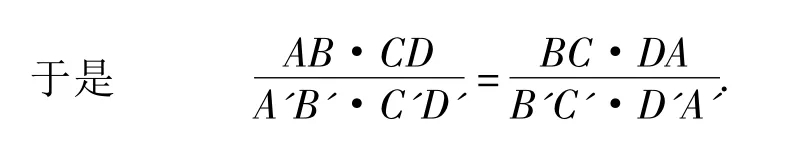
充分性 当A',B',C',D'为正方形的4个顶点时,显然AB·CD=BC·DA.
必要性 当AB·CD=BC·DA时,由PA·PA'=PB·PB'=PC·PC'=PD·PD'=k,可视点 A,B,C,D 的反演点为 A',B',C',D'.由反演变换的性质,可知 A',B',C',D'在 AB·CD=BC·DA的条件下为一正方形的4个顶点.
注由性质8给出了作调和四边形的又一种方法.在文献[2]中,也有如下定义:如果一个四边形的顶点是一个正方形顶点的反形,那么被称为调和四边形.
性质9 圆内接四边形为调和四边形的充要条件是其一顶点对其余三顶点为顶点的三角形的西姆松线段被截成相等的两段.
证明如图2,设ABCD为圆内接四边形,不失一般性.设点D在△ABC的3条边BC,CA,AB上的射影分别为L,K,T,则LKT为点D的西姆松线段.此时 L,D,K,C 及 D,A,T,K 分别四点共圆,且CD,AD分别为其直径.设此圆的半径为R,由正弦定理得
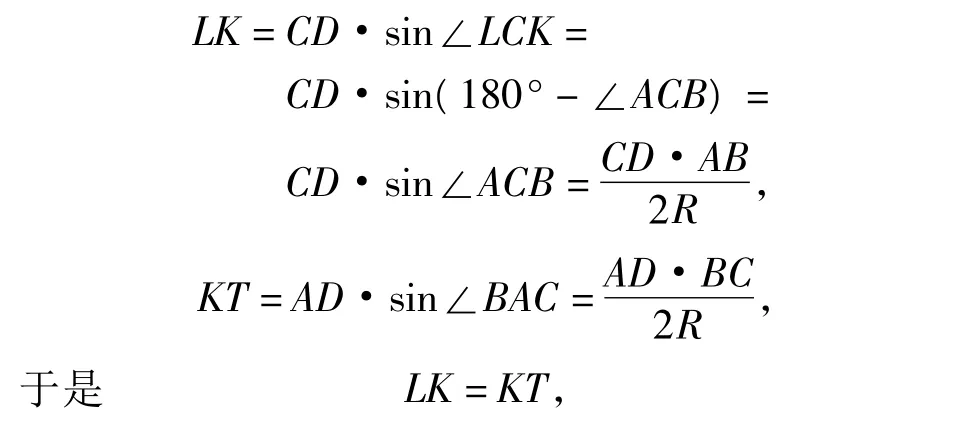

从而四边形ABCD为调和四边形.
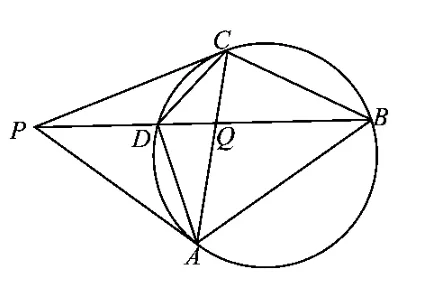
图3
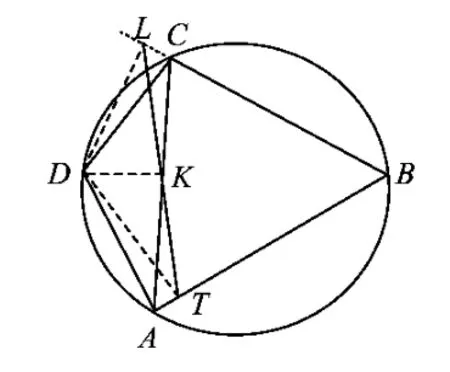
图2
性质10 圆内接四边形为调和四边形的充要条件是一条对角线2个端点处的切线交点(或无穷远点)与两对角线的交点调和分割另一条对角线.
证明当圆内接四边形为筝形时,易证得结论,这留给读者自行证明.下证非筝形时的情形.
如图3,设圆内接四边形ABCD的2条对角线相交于点Q,在A,C处的2条切线相交于点P.由△QCD∽△QBA,△QAD∽△QBC,得
充分性 如图3,当P,Q调和分割DB时,
此时点P,D,Q,B共线.由△PDC∽△PCB得
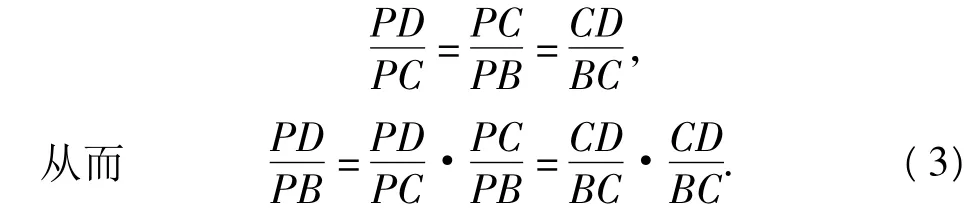
又由式(1),(2),(3)得
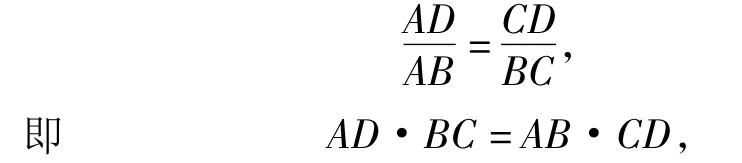
于是四边形ABCD为调和四边形.
必要性 如图3,当ABCD为调和四边形时,由性质1,知点 P,D,Q,B 共线,且有式(3)成立.由AD·BC=AB·CD,得
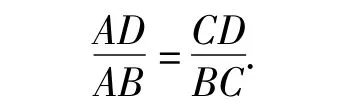
再注意到式(1)与式(3),得
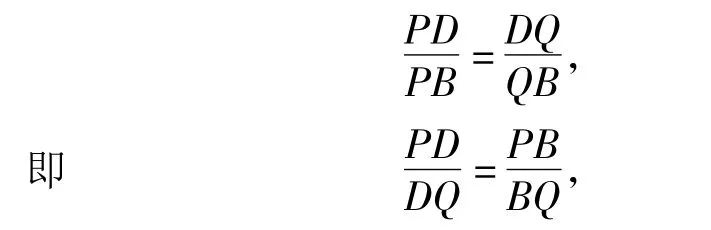
于是点P,Q调和分割DB.
性质11 圆内接四边形为调和四边形的充要条件是2条邻边之比等于此2条邻边所夹对角线分另一条对角线为2段对应之比开平方.
证明如图4,设圆内接四边形ABCD的2条对角线AC与BD交于点Q.
当圆内接四边形为筝形时,易证得结论,这也留给读者自行证明.下证非筝形时的情形.
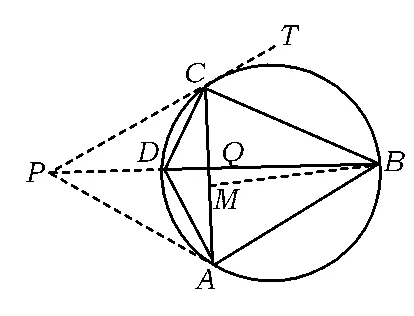
图4

从而ABCD为调和四边形.
必要性 当ABCD为调和四边形时,由性质1,知点A,C处的切线与直线DB共点于P,如图4.于是,注意到面积关系与正弦定理,得
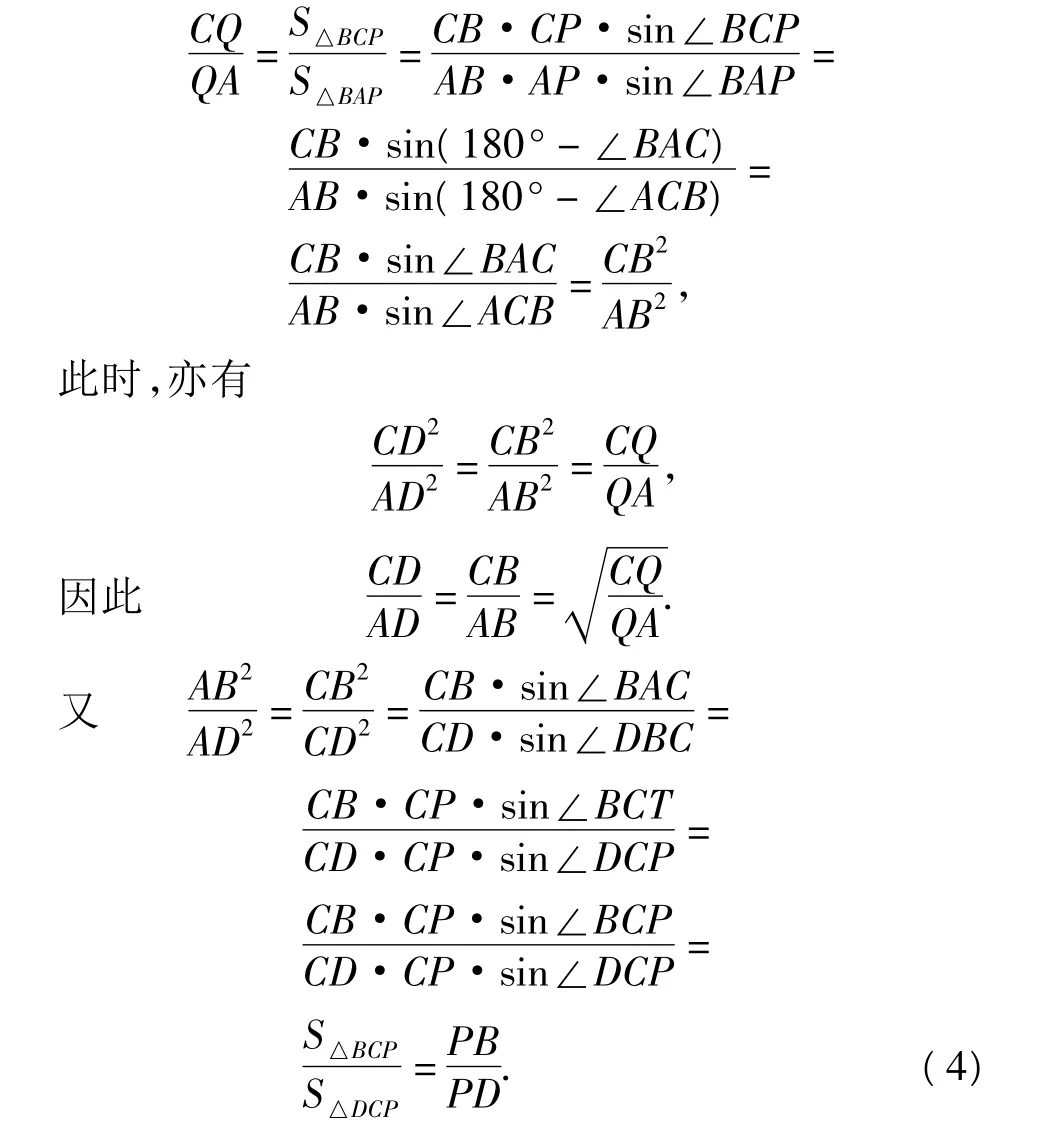
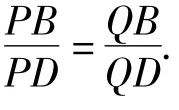

注由性质4知,在调和四边形中,对角线的中点是其等角共轭点.如图4,设M为AC的中点,

性质12 在调和四边形ABCD中,点P在对角线 BD上,记 O,O1,O2分别为四边形 ABCD,△BCP,△ABP的外接圆圆心,则直线BO平分线段O1O2.
证法1 如图5,联结BO1,BO2,OO1,OO2.设 M 为AC的中点,则由调和四边形的 性 质 4,知 ∠ABP =∠CBM,即∠ABM=∠CBP.
设直线BO交O1O2于点Q,此时
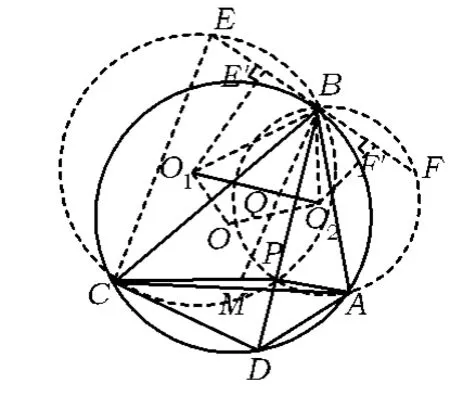
图5
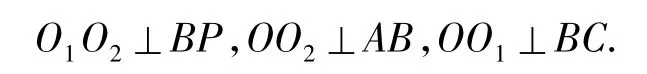
注意到当一个角的2条边与另一角的2条边对应垂直时,这2个角相等或相补,得
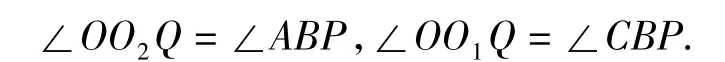
于是,由正弦定理得
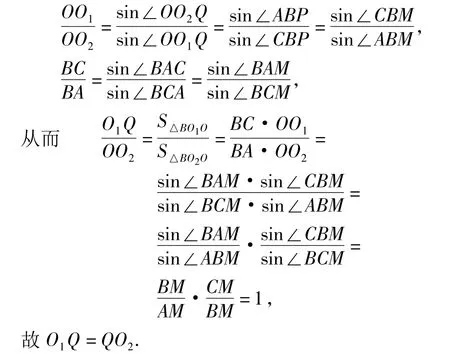
证法2 如图5,设M为AC的中点.由性质4,知∠CBM=∠ABP,即∠CBD=∠ABM.又由∠BDC=∠BAM,得△DBC∽△ABM,从而

作△BCP,△ABP的外接圆,过点B作⊙O的切线分别交⊙O1,⊙O2于点 E,F,连结 CE.则由


而MA=CM,于是 BE=BF.作 O1E'⊥EB 于点 E',作 O2F'⊥BF 于点 F'.由垂径定理,知 E',F'分别为EB,BF的中点.在直角梯形O1E'F'O2中,BO即为其中位线所在的直线,故它一定平分线段O1O2.
下面给出一些应用的例子.
例1 设ABCD是一个圆内接四边形,点P,Q和R分别是D到直线BC,CA和AB的射影,证明:PQ=QR的充要条件是∠ABC和∠ADC角平分线的交点在线段AC上.
(2003年第44届IMO试题)
证明如图6,由性质9,知PQ=QR的充要条件是ABCD为调和四边形.又由调和四边形的性质3,知∠ABC和∠ADC的角平分线的交点在线段AC上的充要条件是ABCD为调和四边形.故PQ=QR的充要条件是∠ABC和∠ADC的角平分的交点在线段AC上.
例2 已知直线上的3个定点依次为A,B,C,Γ为过点A,C且圆心不在AC上的圆,分别过点A,C且与圆Γ相切的直线交于点P,PB与圆Γ交于点Q.证明:∠AQC的平分线与AC的交点不依赖于圆Γ的选取. (2004年第45届IMO预选题)
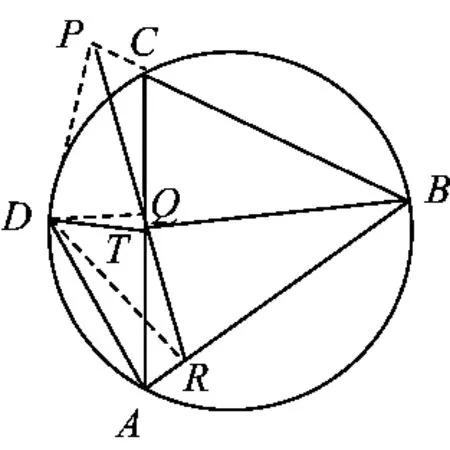
图6

图7
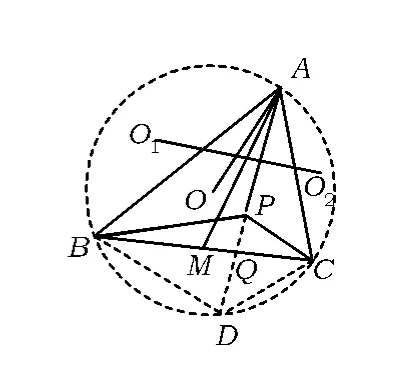
图8
证明如图7,点Q可在劣弧上,也可在优弧上.不失一般性,设点Q在劣弧上,直线PB与圆Γ的另一交点为Q'.由调和四边形的性质1,知AQ'CQ为调和四边形.设∠AQC的平分线交AC于点T,则由角平分线的性质,知.又由性质11,在调和四边形AQ'CQ中,有
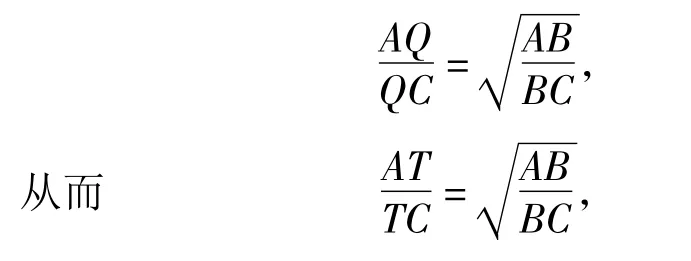
故点T不依赖于圆Γ的选取.
例3 在锐角△ABC中,AB>AC,M是边BC的中点,P是△ABC内的一点,使得∠MAB=∠PAC.设△ABC,△ABP,△ACP的外心分别为O,O1,O2,证明:直线 AO 平分线段 O1O2.
(2010年国家集训队选拔赛试题)
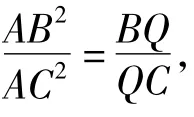
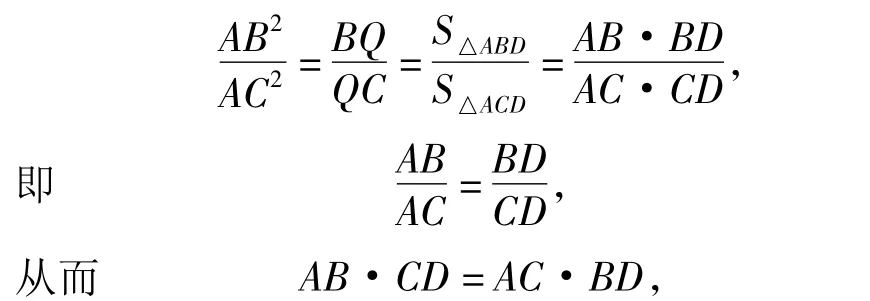
故圆内接四边形ABDC为调和四边形.于是由性质12知直线AO平分线段O1O2.
注由性质12,知例3的条件“P是△ABC内一点”,可改为“P是△ABC的外接圆内一点”,即图8中的线段AD上的点(异于端点)均可.
例4 设锐角△ABC的外接圆为W,过点B,C作W的2条切线,相交于点P.连结AP交BC于点D,点 E,F 分别在边 AC,AB 上,使得 DE∥BA,DF∥CA.
(1)求证:F,B,C,E 四点共圆;
(2)若记过点 F,B,C,E 的圆的圆心为 A1,类似地定义 B1,C1,则直线 AA1,BB1,CC1共点.
(2005年国家集训队测试题)
证明(1)如图9,欲证 F,B,C,E四点共圆,只需证
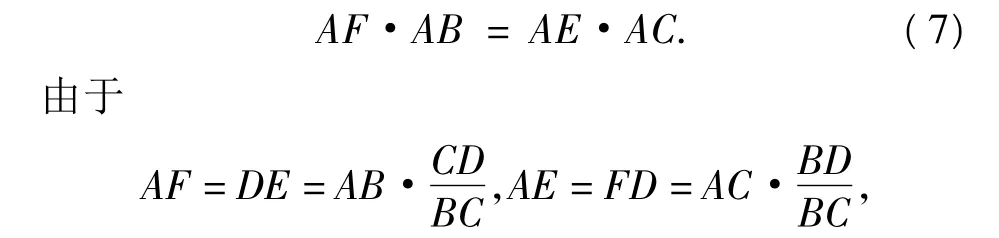
因此欲证式(7),只需证

设AP交圆W于点Q,连结BQ,QC.由调和四边形性质4,知ABQC为调和四边形.由性质11,知在调和四边形ABQC中,式(8)显然成立,故 F,B,C,E四点共圆.
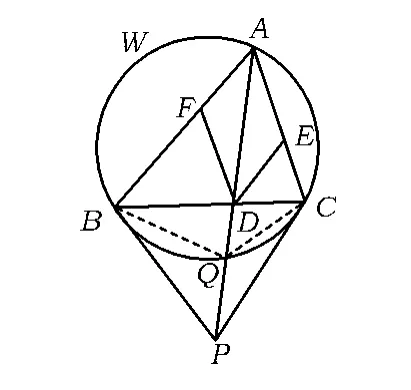
图9

图10

由△AM1N1与△ABC位似,得
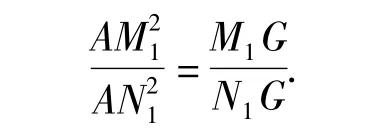
从而由第(1)小题知,F1,M1,N1,E1四点共圆.同理可得,F1,M1,S1,T1及 S1,T1,N1,E1分别四点共圆.于是
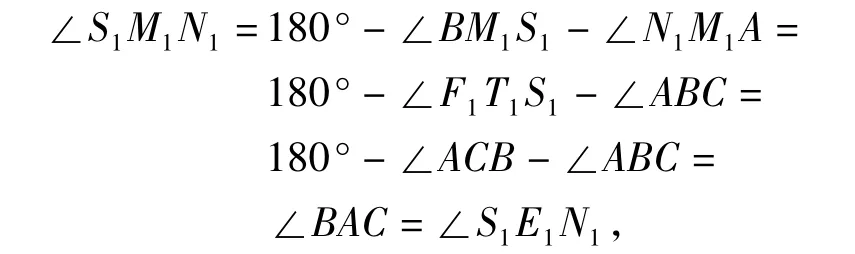
即 M1,S1,T1,N1,E1五点共圆.由对称性,知点 F1也在此圆上,即六点共圆.
设此六点圆的圆心为O.由于⊙OA1与⊙O的位似中心为A,因此直线AA1过点O.同理可得,直线BB1,CC1也过点O.
[1] 沈文选.论调和四边形的性质及应用——兼谈全国高中数学联赛2道加试题的解法[J].中学教研(数学),2010(10):35-39.
[2] 沈文选.几何瑰宝——平面几何500名题暨1 000条定理[M].哈尔滨:哈尔滨工业大学出版社,2010.
