简述三角函数题的7种解法

●邵贤虎 (江浦高级中学 江苏南京 211800)

三角函数是高考和竞赛中的重要内容，属于试题中的基础题.三角函数可以与其他知识综合在一起，演绎精彩的方法.笔者总结了三角函数题的7种解法，供参考.

原题重现 已知角x满足3cosx+4sinx=5，求tanx.

1 回归定义，追本溯源

解法1 设P(a，b)为角x终边上任意一点，点P到原点O的距离为r，则

评析 利用三角函数的定义解题是比较容易忽视的方法，应充分认识定义的解题价值.回归定义，经常会有特别的收获.

2 巧妙配凑，意外惊喜

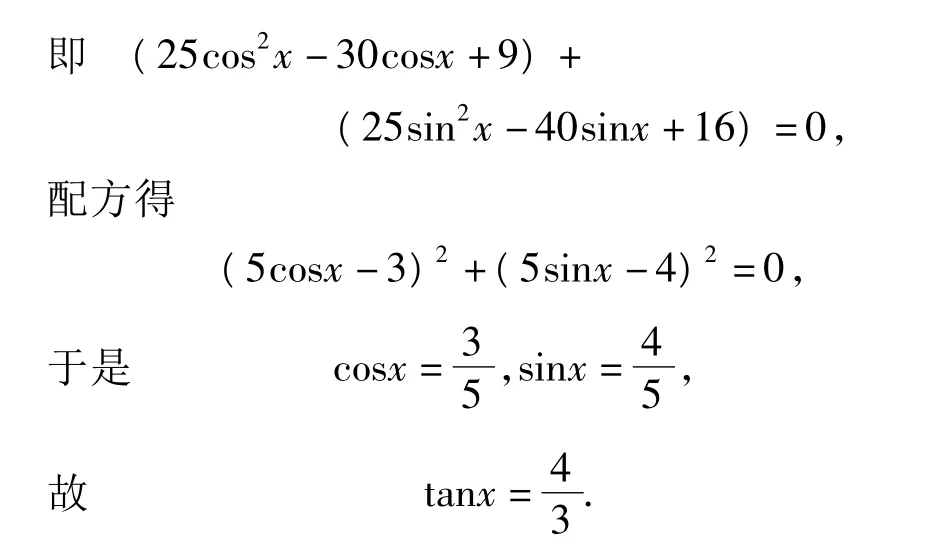
评析 解题是不断尝试的过程，需要信心和敢想敢做的勇气.很多巧解都来源于大胆的想法，始终要相信题目都是“编”出来的!

3 数列登场，良性互动

解法3 因为

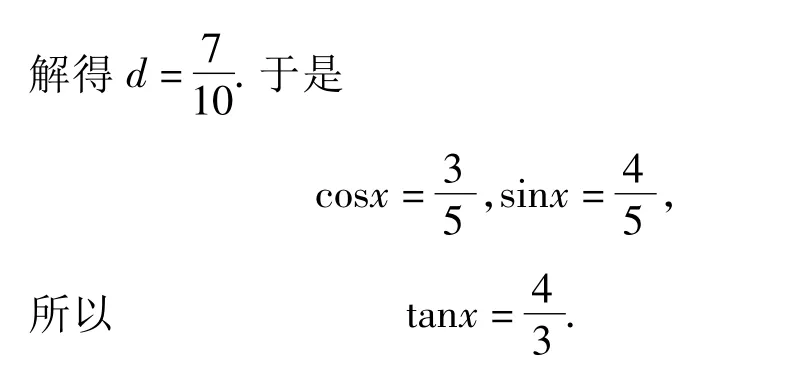
评析 等差数列的出现给三角函数吹入了一股清新的空气，转化为公差的等式可以说是水到渠成.本题告诉我们：知识和方法是相互联系的，可充分发挥各自的优点，为解题服务.

4 巧用对偶，对称和谐

评析 数学中有很多问题有着和谐的对称美，若能善于挖掘与利用这种关系，则往往会有意想不到的收获.在解某些数学问题时，针对其中的式子A的特点，为其配凑一个合适的式子B，使得由A和B之间的运算，能产生一些有用的关系式，促使问题向有利的方向转化，进而解决问题.

5 数形结合，形象直观

解法5 作 Rt△ABC，使得 AC=3，BC=4，则AB=5.作CD⊥AB于点 D，设∠A=α，则∠BCD=α.由图1可得

评析 数形结合就是根据问题的具体情况，把图形性质的问题转化为数量关系的问题，通过代数方法分析数量关系来揭示直观图形的性质，或者把数量关系的问题转化为图形性质的问题，用几何图形直观地刻画数量关系，从而使抽象思维和形象思维结合起来，使抽象问题具体化，最终得到解决.

图1

6 相等问题，不等解决

评析 数学中有些相等问题可以用不等知识来解决.运用三角函数的有界性或均值不等式中等号成立的条件等途径，通过不等导出相等，以此揭示问题中的隐含条件，揭示等与不等矛盾差异的内在联系，使问题得以简洁、明快地解决.

［1］ 俞新龙.新课程教材习题教学的实践探索［J］.中国数学教育，2008(6)：25-27.

［2］ 武瑞雪.三角函数题“正确解法”后的反思［J］.中学教研(数学)，2010(9)：26-29.

［3］ 陈久贵.数学探究的鲜活资源——一道课本习题的探究案例［J］.数学通报，2008(4)：25-27.

［4］ 余锦银.三角函数问题中隐含条件的挖掘［J］.中学教研(数学)，2008(7)：23-25.