例谈不等式研究中的“不妨假定”

●卫福山 (松江区第二中学 上海 201600)

在不等式研究与证明中，经常会使用一些另外增加的“不妨假定”条件，这些附加的条件常常可以降低解题的难度.下面通过一些具体实例谈谈不等式研究中几种常见的“不妨假定”.

1 多元对称不等式中有序的假设

在多元(如三元a，b，c)对称不等式的证明中，可考虑“不妨设”一个有序的假设，譬如a＜b＜c或a≥max{b，c}等等，这相当于增加了一个已知条件，可降低证明的难度.

例1 设 a，b，c均为正数，求证：a3+b3+c3+3abc≥ab(a+b)+bc(b+c)+ca(c+a).

(第9届全苏数学奥林匹克竞赛试题)

分析以上不等式关于字母 a，b，c是对称的，即将(a，b，c)换成(b，c，a)或(c，a，b)，原不等式不变，也即a，b，c的地位均等，因此不妨假设c=min{a，b，c}，为证明带来便利.

证明不妨设c=min{a，b，c}＞0.由于

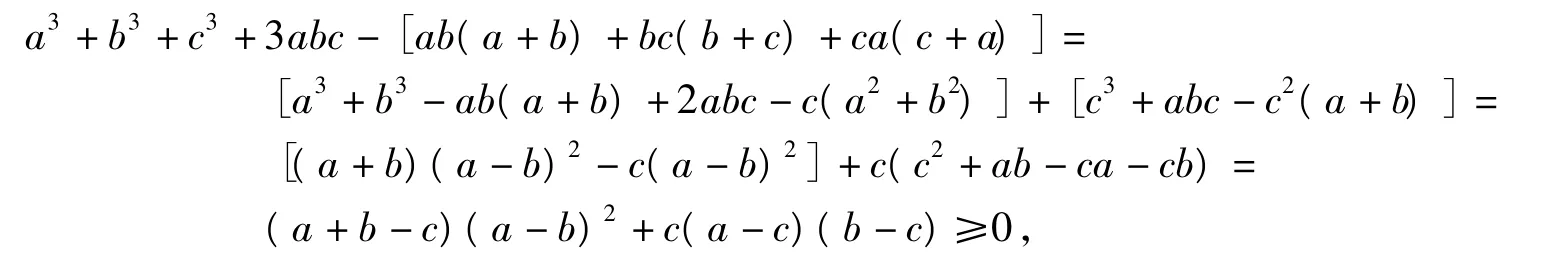
因此原不等式得证.

注以上不等式其实是Schur不等式的特例.Schur不等式如下：

若 x，y，z为非负实数，则对任意 r＞0，都有

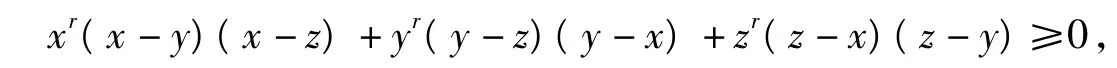
当且仅当x=y=z或者x，y，z中有2个相等，第3个为0时，等号成立.当r=1时，可以得到Schur不等式的特例，即

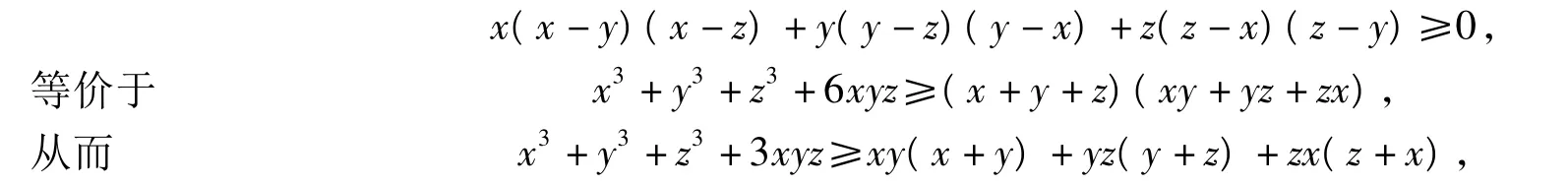
因此，例1即为Schur不等式的特例.

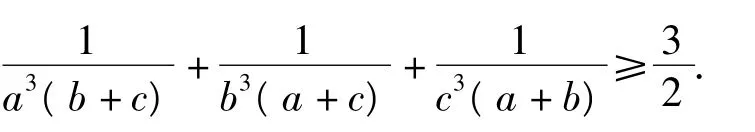
(第36届IMO试题)

分析以上所证不等式具有对称性，不妨假定a≤b≤c，运用排序不等式加以证明.

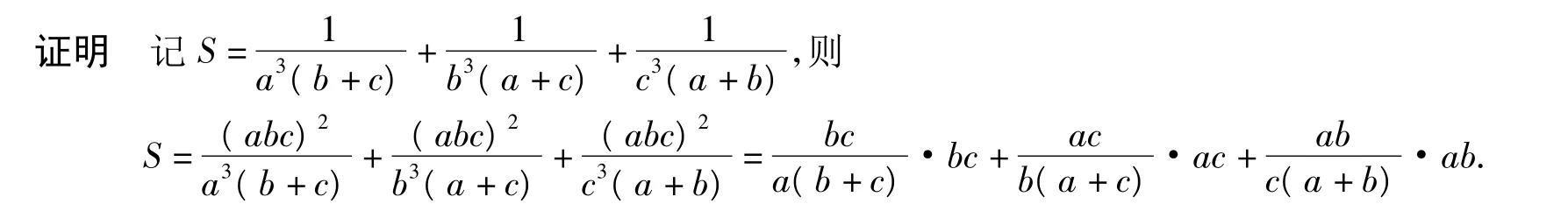
由对称性，不妨设 a≤b≤c，则

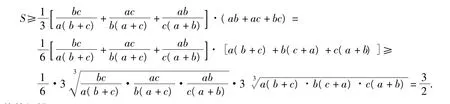
2 和为定值的假设

在某些齐次对称不等式中，若出现几个字母的和的形式(如a+b+c，a+b，b+c，c+a)，假定字母的和为定值(如 a+b+c=k，则 a+b=k-c，b+c=k-a，c+a=k-b)，常会给变形带来便利.

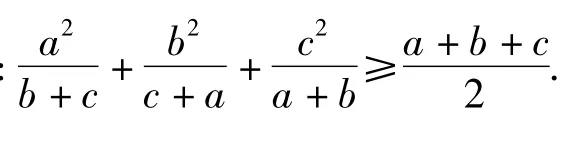
(第2届友谊杯国际数学邀请赛试题)

证明设 a+b+c=s，则

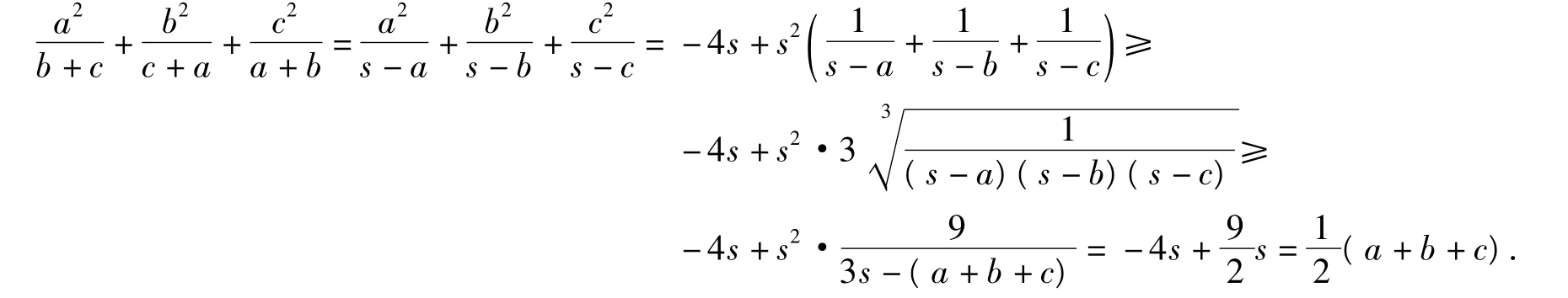
例4 设 a，b，c∈R+，求证：

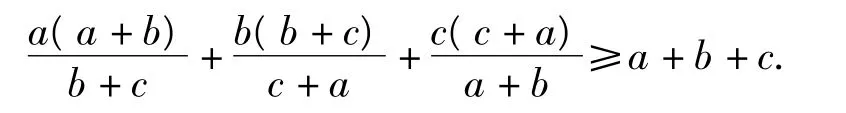
证明令 a+b+c=k，则

3 乘积为定值的假设

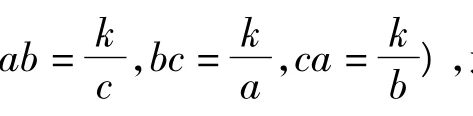
例6 设a，b，c为正数，求证：

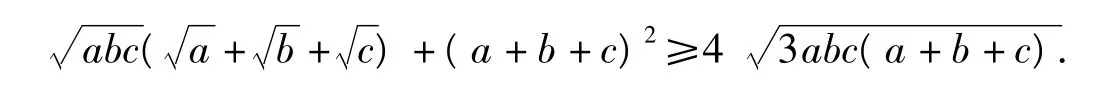
分析不等式2边关于字母a，b，c的次数均为2次，属于奇次对称不等式，不妨假定字母a，b，c的乘积为定值，如abc=1.

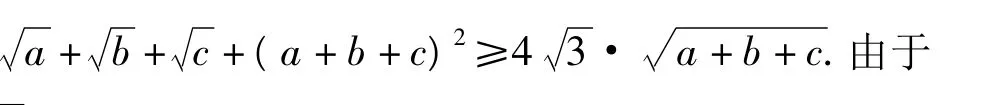
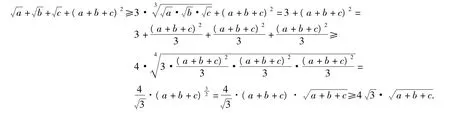
因此原不等式得证.

注本例也可以假设a+b+c=1来简化原不等式，具体如下：

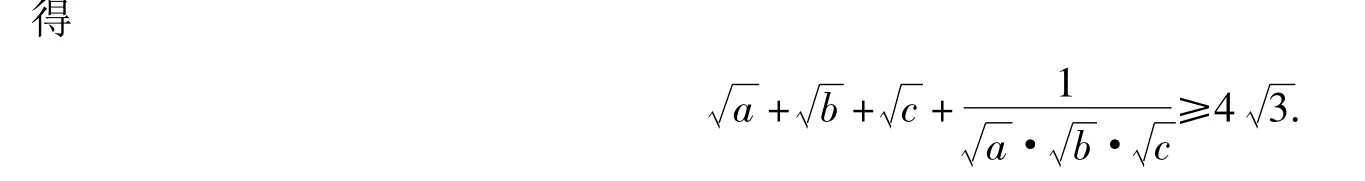
由于a+b+c=1，因此

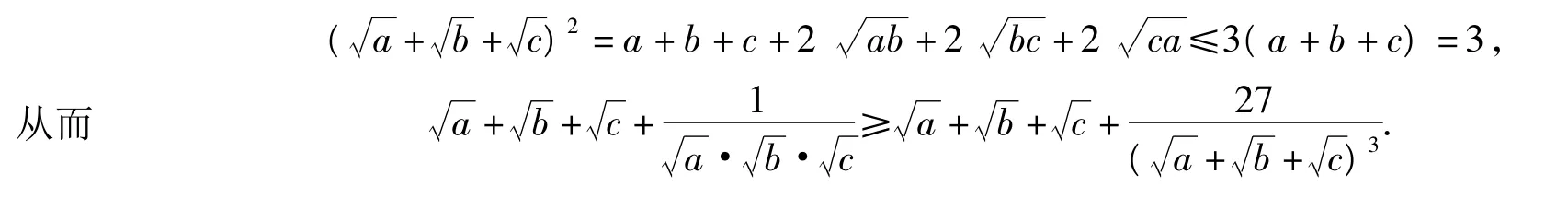
4 三角换元中角的取值范围的假设

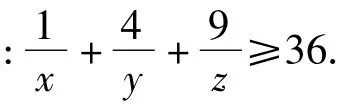
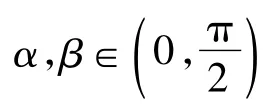
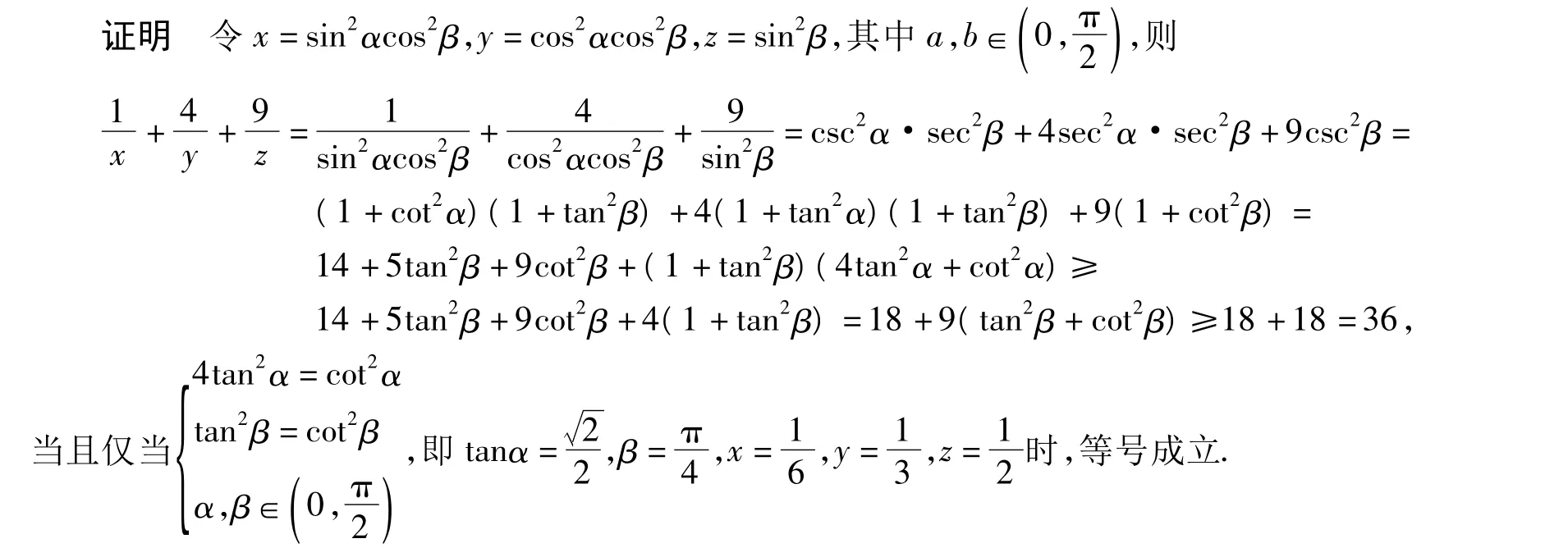
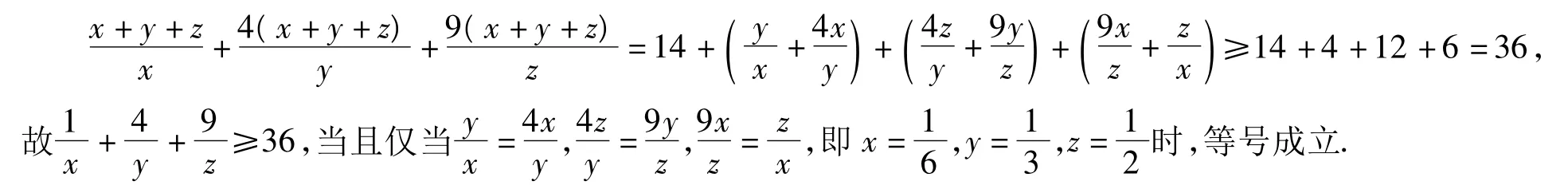
以上证明的难度在于运用均值不等式前“凑”的技巧，这也是学生运用均值不等式的最大难点，显然运用三角换元降低了对此技巧的要求.

［1］ 刘诗雄.奥数教程：高二年级［M］.上海：华东师范大学出版社，2007.