线性条件下的非线性最值问题研究

●张士琴 (汇龙中学 江苏启东 226200)

线性规划研究的是线性目标函数在线性约束条件下最大值或最小值的问题.然而在近几年全国各地的数学高考试卷中，在线性约束条件下求非线性的最值问题已屡见不鲜.该类问题难度较大、解法灵活，是学习上的难点.本文结合近几年的数学高考试题以几个常见的最值问题为例，探求在线性约束条件下的非线性最值问题的求解策略.

A.(1，3］ B.［2，3］

C.(1，2］ D.［3，+∞)

(2010年北京市数学高考试题)

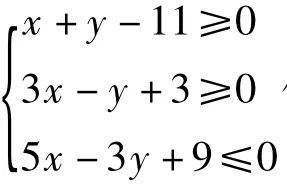
评注本题是线性约束条件下指数函数的最值问题.其解题的一般策略是先作出可行域，再结合指数函数的图像，观察图像得出结果.

图1

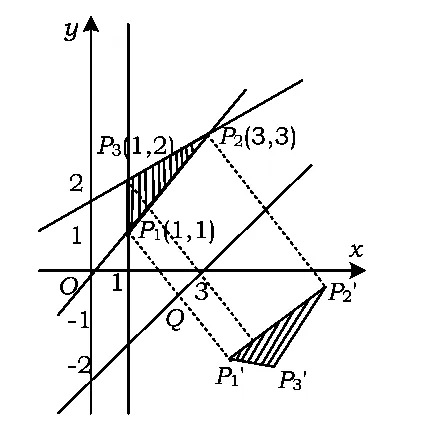
图2

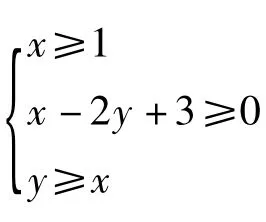
所表示的平面区域是 Ω1，平面区域 Ω2与 Ω1关于直线3x-4y-9=0对称，对于Ω1中的任意点A与Ω2中的任意点B，|AB|的最小值等于 ( )

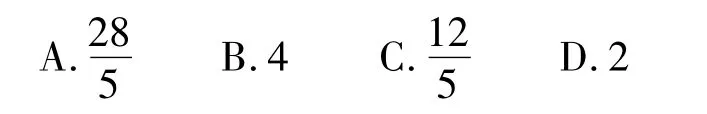
(2010年福建省数学高考试题)

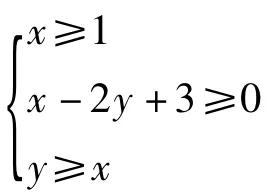
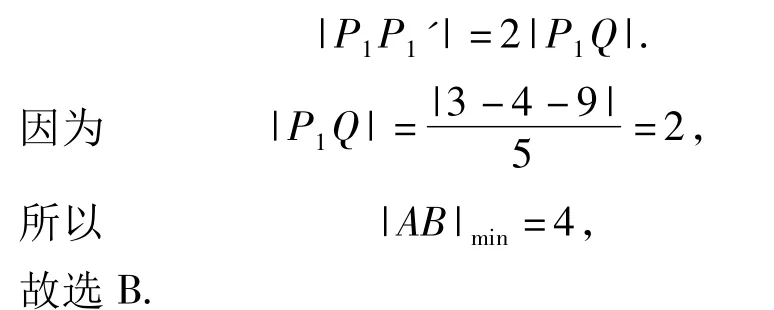
评注本题是2个对称可行性区域中两点之间距离的最值问题.解决这一问题的关键是将|AB|的最小值转化为Ω1中任意点A到直线3x-4y-9=0的距离的最小值，从而使问题得以解决.

例3 实系数一元二次方程x2+ax+2b=0有2个实根，一个根在区间(0，1)内，另一个根在区间(1，2)内.

(1)求点(a，b)对应的区域的面积;

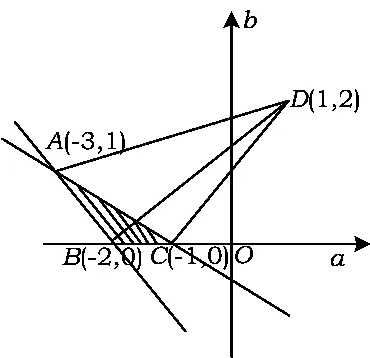
图3

(3)求(a-1)2+(b-2)2的值域.

解设f(x)=x2+ax+2b，方程x2+ax+2b=0的2个根在区间(0，1)和(1，2)内的条件是

在直角坐标系内作出不等式组表示的可行性平面区域(如图 3)，并解出点 A(-3，1)，B(-2，0)，C(-1，0).

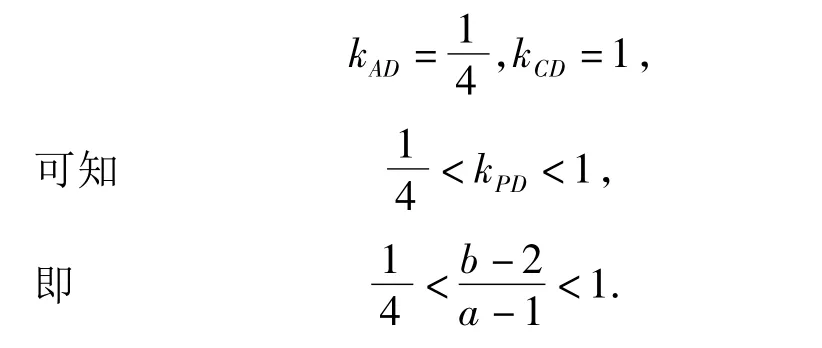
(3)(a-1)2+(b-2)2的几何意义是可行性平面区域内的任意一点P(a，b)与定点D(1，2)之间距离的平方.过点D与AC垂直的直线方程为b-2=2(a-1)，即 2a-b=0.由

所以由图可知

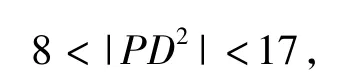
即(a-1)2+(b-2)2的值域为(8，17).

评注本题是线性约束条件下的分式函数和二元二次函数的最值问题.解决这类问题的关键是理解分式函数的几何意义是直线的斜率，二元二次函数的几何意义是两点间距离的平方，由数形结合思想解决问题.

例4 设函数f(x)=x3+3bx2+3cx的2个极值点为 x1，x2，且 x1∈［-1，0］，x2∈［1，2］.

(1)求b，c满足的约束条件，并在图4的坐标平面内，画出满足这些条件的点(b，c)的区域;

(2009年全国数学高考试题)

分析(1)f'(x)=3x2+6bx+3c.由题意知方程 f'(x)=0 有2 个根 x1，x2且 x1∈［-1，0］，x2∈［1，2］，则

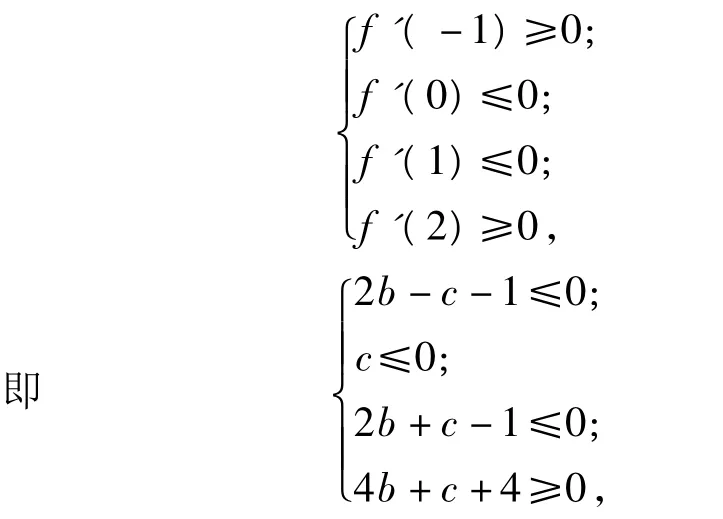
因此可在直角坐标系内作出b，c所满足的约束条件下的可行域(如图5中的阴影部分).

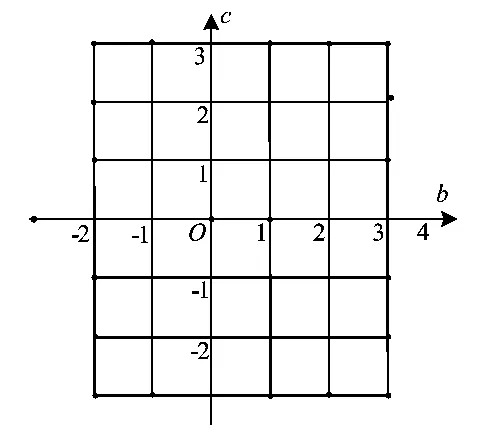
图4

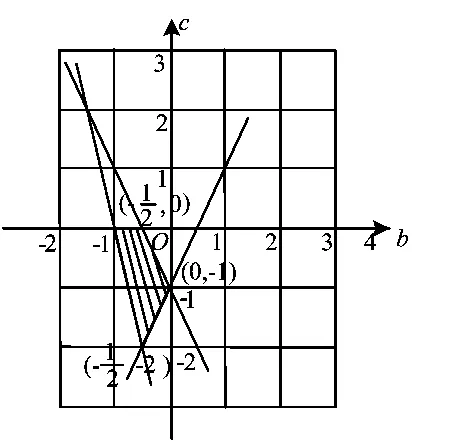
图5

(2)由题意知

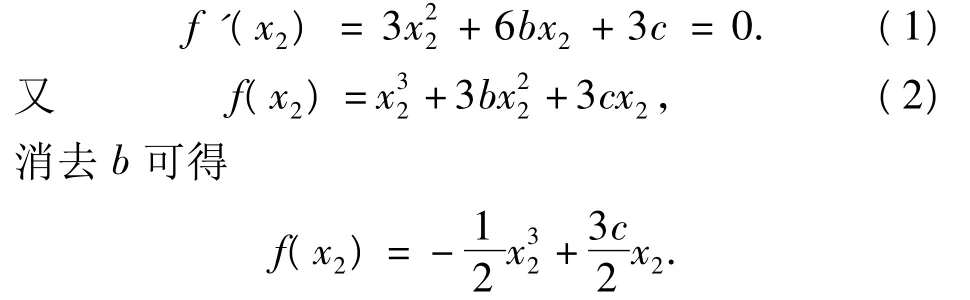
由图5 可知 c∈［-2，0］，因此

从而 f(x2)在［1，2］上单调递减，得

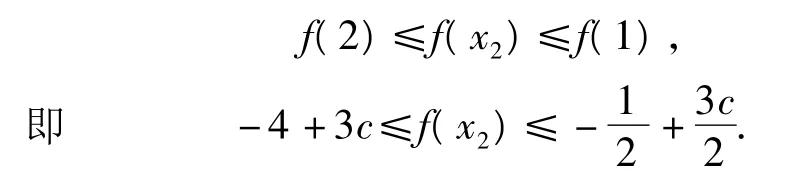
又因为 c∈［-2，0］，所以

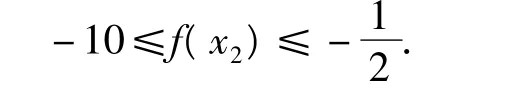
评注本题是线性约束条件下的三次函数的最值问题，对于高次(三次或三次以上)函数的最值，一般可通过导数知识来解决.