对一道数学自主招生题的探究

●金 山 (启东中学 江苏启东 226200)

2008年南京大学数学自主招生考试中有这样一道试题：

问题 若正数a，b，c满足a+b+c=1，求证：

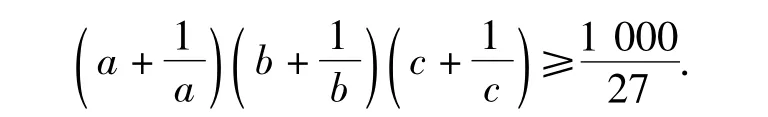
证明由均值不等式得

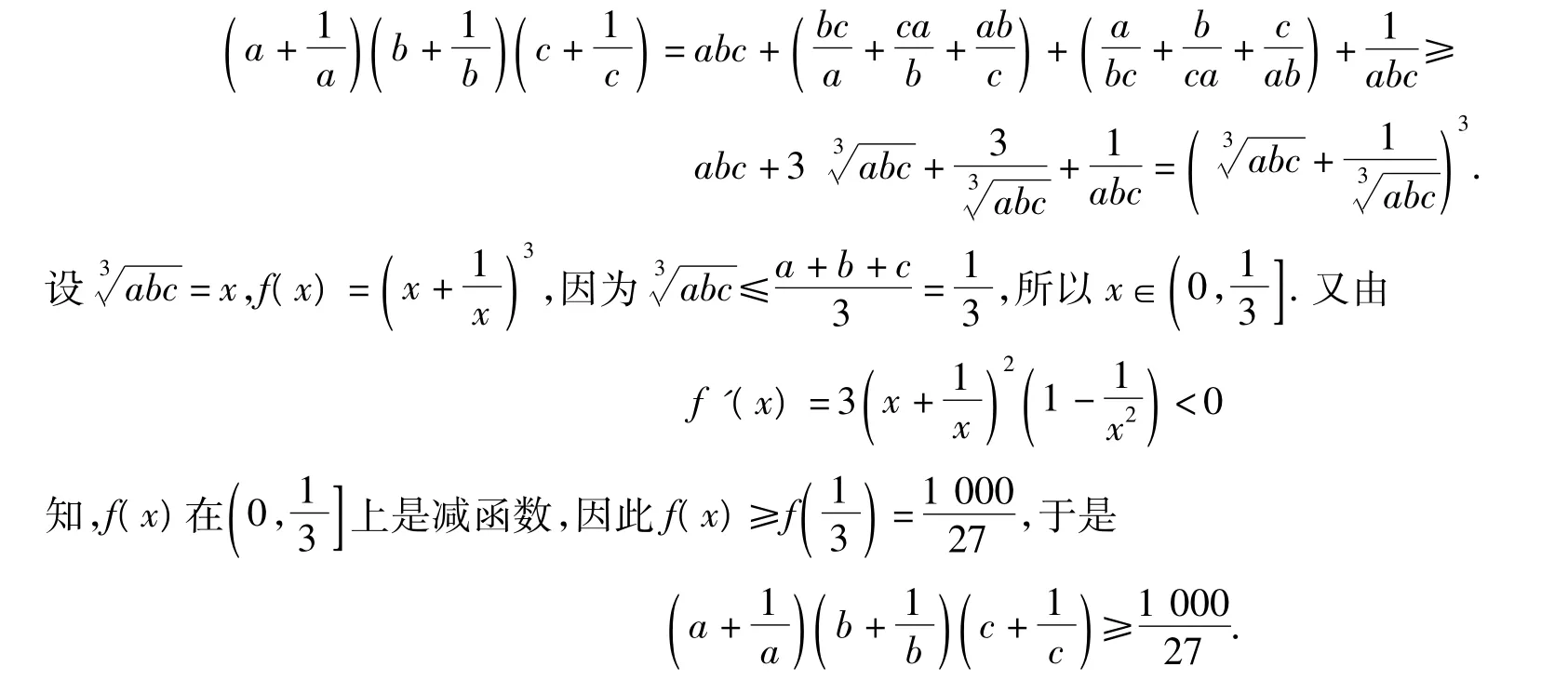
由上述证明过程可知，原不等式可推广为：

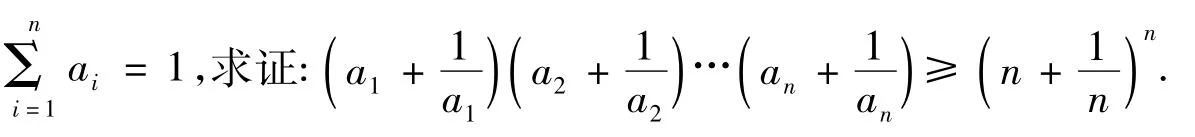
下面给出推广1的另外2种不同的证明方法.

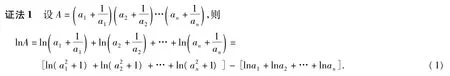
设 f(x)=ln(x2+1)，x∈(0，1)，则

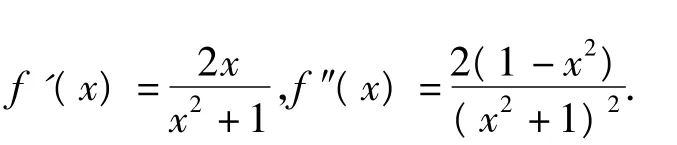
由f″(x)＞0知f(x)在(0，1)上是凸函数，由琴生不等式得

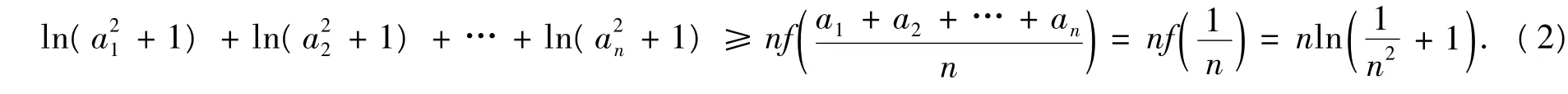
另外，由均值不等式得

把式(2)，式(3)代入式(1)得

故原不等式获证.

证法2 原不等式等价于

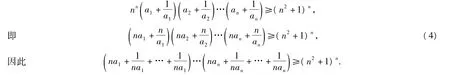
由均值不等式得

代入式(4)左边得

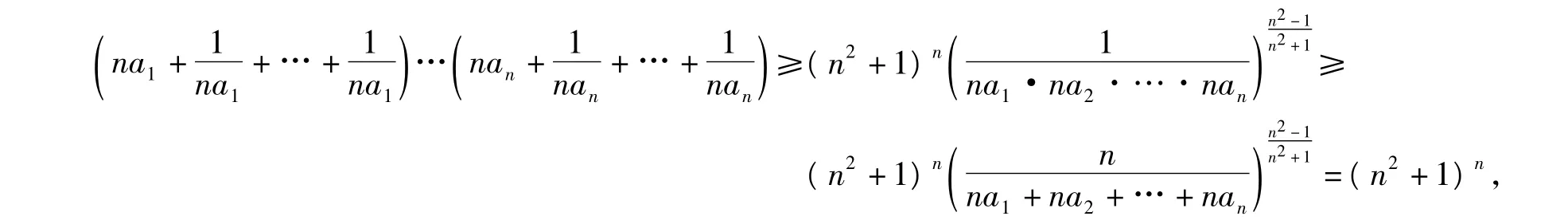
故原不等式成立.

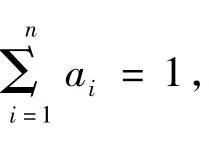
证明首先证明

根据均值不等式得

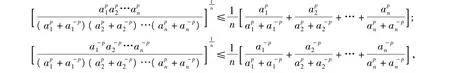
两式相加得

由推广2的证明过程，还可进一步探究得到有关结论：