我国CPI与PPI非线性调整的实证解释

苏梽芳 蔡经汉

（华侨大学数量经济研究院,福建泉州 362021）

一、引言

2008年5月我国PPI超过CPI后两者缺口持续扩大,在CPI不断降低的情况下仍短暂引发了对通货膨胀反弹的担忧。而自2008年11月PPI重新低于CPI后,其在2009年上半年不断走低并加大了与CPI之间的缺口,又使得通货紧缩的压力急剧增加,造成了新的隐忧。作为既有区别又有联系的两种物价指数,PPI常被看作是CPI的一个先行指标,二者背离产生的缺口反映了经济运行的不均衡。2008年以来两者缺口的扩大,可能就预示着经济中存在严重的不均衡现象。由于这种不均衡有可能带来巨大的代价,因此不管对于政策制定者还是普通大众来说,这种不均衡能否及时得到调整值得重点关注。

关于CPI与PPI的关系,已有丰富的理论分析和实证检验。传统的生产环节链条传递观认为,由PPI所衡量的基础商品价格的变化会领先或者说引起由CPI衡量的总体价格指数的变化。但主要从需求角度考虑的另一种观点则认为CPI也会影响PPI,例如Colclough和Lange强调最终消费产品也影响到生产过程中输入品的价格[1]。而Lown和Rich等则从工资上升的角度论证了CPI的上涨会最终拉高PPI[2]。此外,PPI与CPI定义的差异也使得两者关系复杂化。Clark考虑了PPI和CPI指数定义范围不同所产生的问题,他强调,一方面,PPI是完全针对商品的价格指数,而CPI不仅包括商品还包括服务;另一方面,PPI中的一些商品会用于出口,而CPI中则计入了许多进口商品[3]。因此两者理论上具有相互传导关系的结论是模糊的。而在实证检验方面,结论确实也不尽相同。Caporale等研究G7国家的情况发现,在法国和德国是PPI引起了CPI,在美国是CPI引起了PPI,在意大利、日本和英国则有双向的反馈关系[4]。在国内,我国CPI与PPI之间的关系也吸引了众多学者的关注。张延群的研究发现,从短期看是CPI受PPI的影响,而长期来看则是CPI决定PPI[5]。贺力平等分析2001～2007年PPI和CPI的数据发现,CPI是PPI的Granger原因,并认为其主要原因是这期间需求的力量大于供给[6]。也有一些研究应用较独特的计量方法来考察这个问题,如何光辉运用谱分析方法,发现尽管从总量上看CPI和PPI两者之间的关系并不稳定,只有CPI引导PPI,但它们的结构分量之间存在稳定的一致关系,而且无论趋势分量还是周期分量,彼此之间均互为因果,协整一致[7]。肖六亿和常云昆认为2003年以来,垄断性的生产资料市场和竞争性的生活资料市场之间的市场结构差异导致上下游产品的价格不能相互传导[8]。陈建奇则认为非对称供求结构是造成PPI和CPI倒挂的主要原因[9]。

由于PPI到CPI之间的价格传导机制错综复杂,因此两者关系的调整可能是一种非线性过程。首先,从原材料到最终商品的传导过程中可能存在非线性。例如,经济进入上升周期时,原材料价格上升,但企业可能并不会提高产品价格。一方面,企业可能要通过定价策略扩大市场份额;另一方面,在这一阶段劳动力的充分利用甚至生产率的提高反而起到了降低成本的作用。政府管制、汇率与进出口的变化等等都会导致在原材料到最终商品的过程中价格不会成比例上升,即可能存在非线性关系。其次,在商品和服务之间也可能存在非线性关系。发达国家的经验显示,服务价格通常比商品价格上涨得更快,两者之间存在的缺口可能会影响到整体通货膨胀的宏观调整机制,从而造成非线性调整。例如Esteve等分析美国的核心通胀数据发现,商品价格指数与服务价格指数之间确实存在非线性协整关系[10]。

综上所述,国内外研究之所以出现迥然不同的结论,可能正是因为忽略了在PPI向CPI传导的过程中可能存在非线性协整关系,即向长期均衡的调整并不一定在每个时刻都能发生。相反,更有可能的是,只有在PPI和CPI之间的缺口大于某一阀值时,它们才会开始调整,最终回到长期均衡位置。而从我国PPI与CPI的走势来看,当两者存在较大偏离时,随后都会有一个修正的过程。鉴于此,本文将采用Hansen和Seo提出的两区制门槛误差修正模型[11],试图描述和解释PPI与CPI倒挂后恢复均衡的过程。该模型很好地刻画了由PPI与CPI组成的系统在趋向长期均衡关系的过程中存在的非线性调整特点:当对均衡的偏离小于或等于门槛值时,倾向于不向均衡状态调整;而当对均衡的偏离大于门槛值时,倾向于向均衡状态调整。

二、模型方法

Hansen和Seo在门槛协整基础上,提出了一种以误差修正项为门槛变量的两区制门槛误差修正模型,发展了LM检验方法并把它用于检验门槛效应的存在性,并给出门槛值未知情况下的模型参数估计方法。

一个滞后阶数为l的两区制门槛协整模型表示如下:

其中 ,Xt-1（β）={1,w t-1（β）,Δxt-1,Δxt-2…Δxt-l}′,xt是 p维一阶单整时间序列,即I（1）过程 ;β是p×l维的协整向量,w t=β′xt是I（0）过程的误差修正项,ut是误差项,A1和A2是描述两个区制动态变化的系数矩阵,γ为门槛参数。进一步,H ansen和Seo用LM检验方法检验模型是否存在显著的门槛效应。零假设H 0:应用线性误差修正模型拟合变量之间的动态关系,即不存在门槛效应;备择假设H l:应用非线性误差修正模型拟合变量之间的动态关系。针对协整向量已知和未知两种情况,Hansen和Seo提出两个不同的LM检验统计量,在真实协整向量已知情况下,定义检验统计量为:

其中,˜β为式（1）中参数β的估计值,[γL,γU]为设定的γ值的搜索区间,γL和γU分别为的ø和（1-ø）百分位点。And rew s建议ø的设置在0.05和0.15之间[12]。对于上述两种检验,H ansen和Seo建议都采用Bootstrap法获得LM检验的临界值和P值。

三、实证分析

本文选择消费者价格指数（CPI）和工业品出厂价格指数（PPI）的月度同比数据作为样本数据,样本区间为2000年1月至2009年9月,共117组样本数据。数据来源于中国经济信息网数据库。通过描绘CPI与PPI的时间序列变化趋势图（因篇幅限制,故省略）,我们不难发现CPI和PPI确实发生过数次较大偏离,但从长期看,两者走势具有相似性,即短期内存在偏离,但却可能存在长期稳定的协整关系,而这需要应用协整技术进行检验。

（一）单位根检验

在检验协整关系之前,首先应对CPI与PPI进行平稳性检验,进而确定这两个时间序列的单整阶数,单位根检验结果列在表1中。

而当协整向量未知时,检验统计量为:

表1 单位根检验结果

从表1的结果不难发现,对于变量CPI与PPI的水平项,ADF、PP单位根检验结果均显示,在1%的水平下,相应的统计值均不显著,因此无法拒绝单位根存在的零假设。而对于其一阶差分序列,在1%的水平下,均一致拒绝存在单位根的零假设,即CPI与PPI的一阶差分序列为平稳序列,这表明CPI与PPI同为一阶单整过程,即I（1）。

（二）协整检验与线性误差修正模型

由于CPI与PPI同为I（1）过程,因此两者的某种线性组合可能为平稳序列,即CPI与PPI可能存在长期稳定的协整关系。为了与非线性门槛误差修正模型得到的结论相比较,本文采用Johansen协整法检验CPI和PPI之间是否存在线性协整关系。由于Johansen协整检验结果对滞后阶数比较敏感,本文使用AIC、SC信息准则和LR统计量作为最优滞后阶数的检验标准,最后确定VAR模型的最优滞后阶数为1。Johansen协整检验得出的结果列在表2中。

表2 Johansen协整检验结果

表2的检验结果显示,零假设“0个协整向量”的迹统计量为11.354,大于10%的临界值,它犯第一类错误的最大概率是0.072,概率较小,至少在90%的置信水平下拒绝原假设。而相比之下,零假设“至多有1个协整向量”的迹统计量小于10%的临界值,假设无法被拒绝,表明CPI和PPI之间存在1个协整关系。进一步,可以得到向量误差修正模型如下（括号内数值为t值）:

从模型的估计结果看,式（4）与式（5）的误差修正系数一负一正,符合负向反馈机制。从系数绝对值来看,PPI的修正幅度大于CPI的修正幅度。对CPI而言,如果它上一期偏离长期均衡关系,那么本期只有0.2%得到纠正,而且调整效果并不显著。而对PPI而言,如果它上一期偏离长期均衡关系,那么本期会有8.15%得到纠正,而且调整效果非常显著。上述结果表明CPI与PPI之间的缺口缩小,主要是由PPI的调整而得以实现,但是这种调整过程比较缓慢,平均而言需要大概一年左右的时间（1/0.0815=12个月）。

（三）门槛模型估计结果与解释

上述线性误差修正模型可能忽略系统调整的非连续性。因此,本文进一步使用H ansen和Seo提出的门槛协整模型对是否存在门槛效应进行检验。由于在不同的滞后期下,模型检验结果会有差异,因此本文假定模型的最大滞后期为4,依次选择不同滞后阶数进行协整检验,以AIC值最小为最优模型。Sup LM门槛检验使用Bootstrap方法,其中Bootstrap次数取2 000次,估计与检验结果列在表3中。

表3 门槛协整模型估计与检验结果

由表3可知,不管是以AIC值最小还是BIC值最小为标准,门槛协整模型的最优滞后阶数都应取1,此时AIC值为 -1 124.763,BIC值为 -1 123.852。最优模型的Sup LM检验统计值为19.884,对应的P值为0.021,即拒绝线性模型的假设,可认为具有门槛效应。由此可以判定,我国CPI与PPI之间存在门槛效应。此时,模型估计得到的门槛值为 -0.02,而协整向量为1.058,这意味着区制一的条件是w t=CPIt-1.058PPIt≤-0.02,即CPI小于PPI约两个百分点的时候,此时全部样本观测值中处于这一区制的比例是31.6%。相应地,区制二的条件即为 wt=CPIt-1.058PPIt＞-0.02,全部样本观测值中处于这一区制的比例是68.4%。误差修正项w t随时间变化的趋势见图 1。从图 1可知,误差修正项处于区制一时,系统基本处于CPI和PPI倒挂较严重的阶段,而误差修正项处于区制二时,CPI和PPI的关系较正常。因此,我们将区制一定义为CPI和PPI的倒挂期,而将区制二定义为正常期。

图1 误差修正项与PPI

进一步,在选定最优模型设置下,借助门槛效应的Wald检验可以确定门槛效应究竟是来自于动态系数还是误差修正系数。表4所列出的检验结果表明,在10%水平下,两者都是显著的。这就说明不管是动态系数还是误差修正系数,在不同区制下确实是不同的。这一检验结果有力地支持了门槛效应的存在。

表4 门槛效应检验

最终估计得到的门槛误差修正模型表示如下:

为了考察不同区制下CPI与PPI对误差修正项的反应,从而了解不同区制下误差修正收敛速度的差异性,本文将变量CPI和PPI的一阶差分ΔCPIt、ΔPPIt视为误差修正项的函数,在其他变量保持不变的情况下,绘制出图2。结合图2与式（6）、（7）,本文有下面三点发现:

第一,在不同区制下,CPI和PPI存在非对称调整。从绝对量的意义上来说,在区制一时,PPI方程中误差修正项的系数为0.238,而CPI方程中误差修正项的系数仅为0.046,PPI的调整速度远大于CPI,而在区制二时则是CPI的调整速度大于PPI。但应该注意的是,只有在区制一时PPI方程中的误差修正系数才是显著的,而区制一时CPI方程中的误差修正系数以及区制二时两个方程的误差修正系数皆不显著。这一结果从图2中也可看出,CPI向下调整而PPI往上调整,且 PPI调整的速度大于CPI调整的速度,也就是说PPI对误差修正的反应较为快速。

第二,在趋向长期均衡位置的短期调整过程中,调整主要是由PPI来完成的,并且这种调整主要发生在区制一,即CPI和PPI的倒挂期。此时,CPI与PPI的缺口较大,系统会产生拉动PPI向下的力量。在倒挂期,PPI的调整速度相当快,对于上一期所产生的短期偏离,在本期会有23.8%得到纠正。这种调整平均而言需要大概四个月左右的时间（1/0.238=4个月）。可以看到,与线性模型的结果相比,门槛协整模型确实更好地描述了短期内的变化。对于较大的偏离,系统会在短期内进行较剧烈的调整,而线性模型无法反映这种短期内的调整特点。

第三,在不同的区制内,PPI与CPI之间的Granger因果关系方向不一致。在线性误差修正模型中,CPI方程中的各项系数皆不显著,这说明PPI不是CPI的Granger原因。而PPI方程中的各项系数均是显著的,这说明CPI是PPI的G ranger原因。然而,从门槛误差修正模型的估计结果中,我们进一步发现,在区制一时,CPI方程中的误差修正系数以及ΔPPIt-1的系数都不显著,这说明在区制一中PPI不是CPI的短期Granger原因。而PPI方程中虽然ΔCPIt-1的系数不显著,但误差修正系数是显著的,这说明在区制一中CPI是PPI的短期Granger原因。而在区制二时,CPI方程和PPI方程中相应的两个动态系数都很显著,这表明在区制二中CPI和PPI互为G ranger原因。

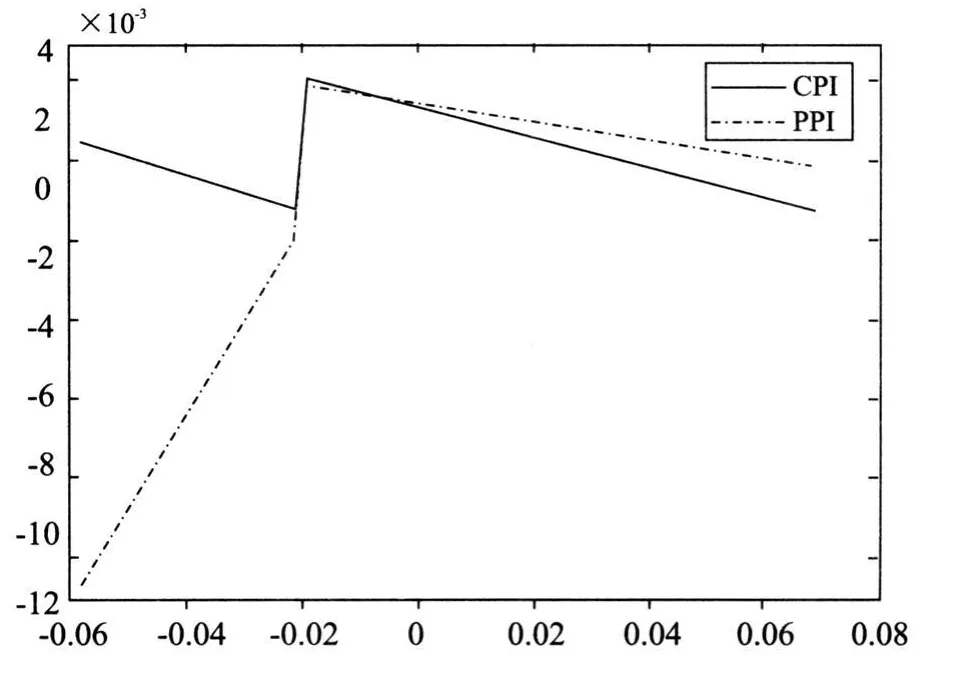
图 2 CPI与PPI对误差修正项的反应

四、结论

本文基于两区制误差修正模型,对我国CPI与PPI的倒挂现象进行了实证分析,结果发现:尽管我国在短期内经常存在CPI和PPI倒挂现象,但两者仍然存在长期均衡的稳定关系;短期偏离只有在超过某种程度时,系统才开始向长期均衡位置调整,而且调整呈非线性特点。本文所使用的门槛误差修正模型很好地刻画了这一调整过程,模型估计得到的基本结论如下:

第一,CPI与PPI之间存在非线性协整关系。门槛效应检验结果表明显著存在门槛效应,而且同时存在于动态系数和误差修正系数中,估计得到的门槛值为 -0.02。在门槛值左、右两边不同区制内,CPI和PPI的调整速度并不一致。在区制一时,PPI的调整速度大于CPI的调整速度,即PPI对误差修正的反应较为快速。

第二,在回到长期均衡位置的短期调整过程中,调整主要是由PPI来完成的,而且这种调整主要发生在区制一,即CPI和PPI发生倒挂的时期。此时,CPI与PPI的缺口较大,系统会产生拉动PPI向下的力量。

第三,在不同的区制中,CPI和PPI存在不同的Granger因果关系。在区制一时仅存在从CPI到PPI的单向Granger因果关系;而在区制二时存在CPI和PPI的双向G ranger因果关系。

[1]Colclough,W.G.,Lange,M.D.Empirical Evidence of Causality from Consumer to Whole Sale Prices[J].Journalof Econometrics,1982,19（2）:379—384.

[2]Low n,C.S.,Rich,R.W.Is There an In flation Puzzle?[Z].Federal Reserve Bank of New York Research Paper No.9723,1997.

[3]Clark,T.Do Producer Prices Lead Consumer Prices?[J].Econom ic Review,1995,（3）:25—39.

[4]Caporale,G.M.,Katsimi,M.,Pittis,N.Causality Links between Consumerand Producer Prices:Some Empirical Evidence[J].Southern Economic Journal,2002,68（3）:703—711.

[5]张延群.商品价格指数是消费价格指数的前导变量吗?[J].数量经济技术经济研究,2007,（12）:140—149.

[6]贺力平,樊纲,胡嘉妮.消费者价格指数与生产者价格指数:谁带动谁?[J].经济研究,2008,（11）:16—26.

[7]何光辉.中国CPI与 PPI的结构与动态作用机制研究[J].经济科学,2009,（4）:15—30.

[8]肖六亿,常云昆.价格传导关系断裂的根本原因分析[J].中国物价,2005,（12）:18—21.

[9]陈建奇.PPI、CPI倒挂与通货膨胀调控——基于非对称供求结构与价格决定机制的实证研究[J].中国工业经济,2008,（11）:24—34.

[10]Esteve,V.,Pareja,S.G.,Serrano,J.A.M.,Vivero,R.L.Thresho ld Cointegration and Non linear Ad justment betw een Goods and Services Inflation in the United States[J].Econom ic Modelling,2006,23（6）:1033—1039.

[11]Hansen,B.E.,Seo,B.Testing for Two-regime Thresho ld Cointegration in Vector Error-correction Models[J].Journa l of Econometrics,2002,110（2）:293—318.

[12]Andrew s,D.W.K.Tests for Parameter Instability and Struc tural Change with Unknown Change Point[J].Econometrica,1993,61（4）:821—856.