基于降维子空间的多重信号分类快速算法
2010-08-21李国林程国标
谢 鑫,李国林,程国标
(1.海军航空工程学院,山东烟台 264001;2.91960部队,广东汕头 515073)
0 引言
近炸引信技术的发展方向之一在于探测的精细化,拥有空间精确定位能力则是其中的一个具体目标。目前引信普遍采用的传统天线体制在提高空间定位能力上已经遇到了瓶颈,比较而言,阵列天线在这一方面则具有先天的优势。然而阵列天线的体积和复杂的数据处理要求一度限制着它在弹载乃至机载平台的应用。随着共形天线技术的发展,在导弹无线电引信上应用阵列天线正成为可能,这也加速了引信对于快速有效的目标空间定位算法的需求。
空间定位的核心在于到达角(DOA)估计,多重信号分类(MUSIC)DOA估计算法作为主流的超分辨算法之一,自出现以来就一直受到关注,由于其运算量较大,关于降低其运算量的研究也一直在进行。MUSIC算法的运算量主要集中在特征值分解和空间谱的搜索两部分,目前已有的研究也主要集中在这两方面。文献[1—5]分别利用接收数据近似、阵元降维、多级维纳滤波等方法研究了信号子空间或噪声子空间的的快速估计算法,避开了特征值分解问题或简化了运算;文献[6—8]则分别利用FFT、阵元降维和有限域搜索等方法研究了空间谱的快速搜索问题。这些方法不同程度地降低了MUSIC的运算量,但同时多数存在估计精度降低的问题。本文从优化MUSIC搜索过程的角度研究降低MUSIC的运算量的方法,提出了一种基于降维子空间的快速搜索算法。
1 阵列信号模型
考虑一个由N个阵元组成的扇形阵列,扇形张角为φ0,扇形半径为R,各阵元沿扇形均匀排列,阵元的归一化方向图函数均为G(θ),方向图指向扇形阵列外部如图1所示。
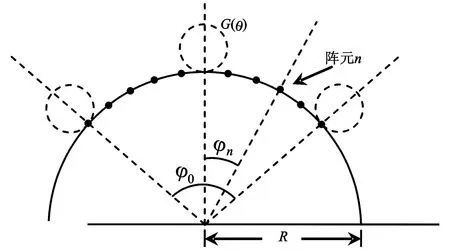
图1 基于有向阵元的均匀扇形阵列Fig.1 Uniform arc array Composed of directional elements
假设接收到M个非相关窄带信号,且N >M,设入射波信号和噪声不相关,则阵列输出信号矢量为:
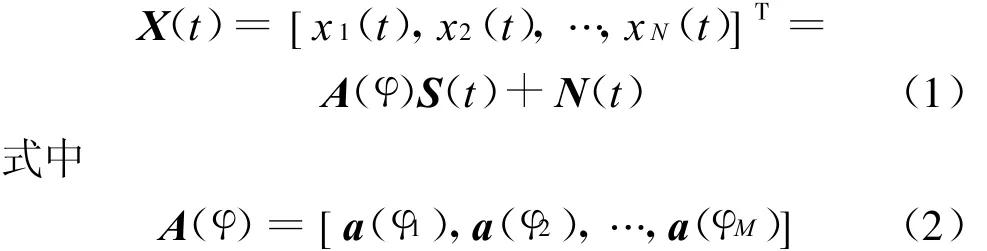
为阵列流形矩阵,其中φi为第i个信号的入射方向,a(φi)为对应的方向向量,且有
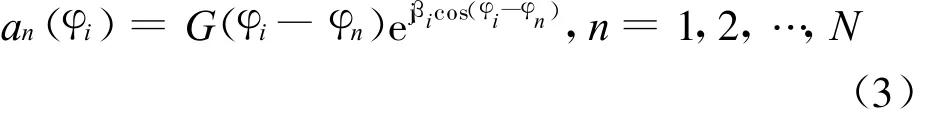
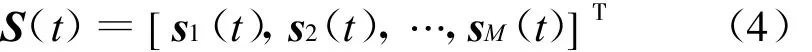
为M个入射信号矢量。
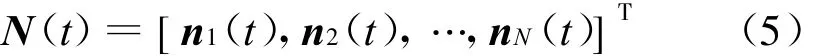
为噪声矩阵,其中ni(t)为第i个阵元中的零均值高斯加性白噪声,方差为σ2。
2 降维子空间搜索算法
基于上一节中描述的阵列模型,可得阵列输出信号的协方差矩阵。
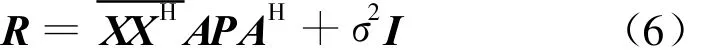
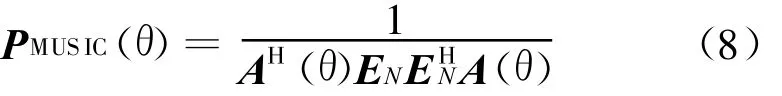
根据式(8),依θ进行步进搜索,并找到谱峰所对应的θ值即为所需的DOA。
从式(8)可以看出,每次步进搜索中,主要为矩阵乘法运算。A(θ)为N×M维矩阵,E N为N×(N-M)维矩阵,在实际编程计算中,一般是通过AHE N(AHE N)H来计算式(8)的,则每步搜索需进行M×(N-M)×(N+M)次复数乘法运算和M×(N2-M2-N)次复数加法运算。
由于E N张成的噪声子空间与信号子空间正交,显然向量eM+1,…,eN都与信号子空间正交。即:
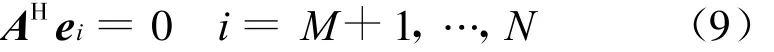
降维子空间搜索就是利用了这一特性,仅从噪声子空间中取出R的一个特征向量进行谱搜索。其空间谱表达式为A的列向量张成的信号子空间正交。即:

MUSIC算法正是利用这一点来进行DOA估计的,其空间谱表达式为[9]:
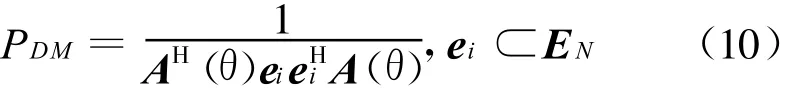
此时,在每次步进搜索中仅需要M ×(N+M)次复数乘法运算和M2次复数加法运算。显然,此时的运算量仅约为标准MUSIC算法的1/(N-M)。由于阵元数量N是要大于入射信号数量M的,且一般情况下(N-M)>1,在弹载引信阵列天线应用中更是如此。因此,运算量降低至原MUSIC搜索算法的1/(N-M)还是相当可观的。
下面给出降维子空间MUSIC算法的具体步骤:
1)计算接收数据的协方差矩阵R;2)进行噪声子空间估计;3)利用式(10)进行空间谱搜索计算;4)利用式(8)对上一步的估计结果进行检验和校正。
3 性能分析和仿真
在降低运算量的同时同样需要关注算法的性能,下面对算法的性能进行分析。令
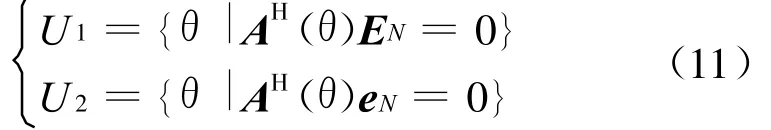
则有:U 1⊆U 2(当且仅当M=N-1时等号成立)
即可能存在某角度θ满足θ∈U且θ∉U 。这也就说明利用这种降维子空间进行DOA搜索可能出现伪峰。出现伪峰的原因正是因为噪声子空间维数的减少使得其正交子空间扩大,从而使得搜索的方向向量落入其正交子空间的概率增大。
利用第2节中的阵列模型,在阵元数为15、快拍数为256、信噪比为10 dB、信号到达角为-20°的情况下,对子空间算法进行仿真计算,其结果如图2所示。
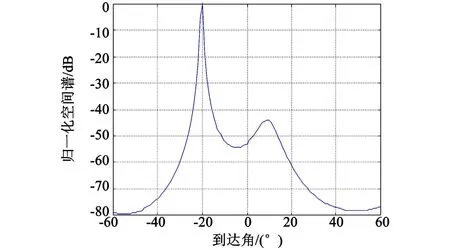
图2 降维子空间算法得到的空间谱Fig.2 Spatial spectrum estimation using dimension reduced subspace algorithm
从图2中可以看出,降维子空间搜索算法能够准确地确定入射信号的到达角,但正如前面所分析的结果,出现了伪峰,这给DOA估计带来了不确定性。通过多次仿真还发现,伪峰出现的位置和数量也具有随机性。在信噪比分别为10 dB和20 d B的情况下,经过200次Monte-Carlo仿真统计实验,得到出现伪峰个数的统计如表1所示。
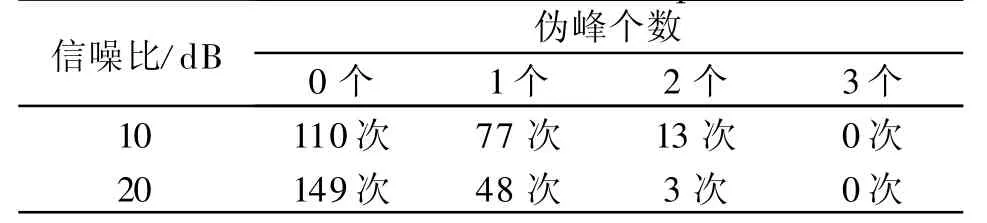
表1 出现伪峰个数统计表Statistic of the amount of false peak Tab.1
从表1可以看出,在10d B信噪比的情况下,出现1个伪峰的概率较高,而出现2个以上伪峰的概率是很低的;而且当信噪比提高到20 dB时,出现伪峰的个数和次数都明显降低。
基于这些统计分析数据,对DOA估计的检验和校正就变得简单了,只需在使用降维子空间算法进行搜索后,对得到的结果再利用式(8)进行检验。根据出现的伪峰个数,这种检验运算一般不会超过M+2次,一般应用中,这个运算次数相对于步进搜索的运算次数是很小,从而不会增加整体运算量。
从上面的分析中可以看出:虽然采用降维子空间进行DOA估计所带来的运算量降低是以引入估计结果的不确定性为代价的,但通过利用标准MUSIC算法进行校正,可以很方便地消除这种不确定性,而且进行这种校正后,还可以保证估计结果在精度上没有任何损失。
4 算法运算量分析
在第3节中已对降维子空间搜索算法和标准MUSIC算法的运算量进行了简单对比。为了具体地说明问题,下面将对不同阵元数目、不同目标数目的情况下两种算法搜索过程的运算量进行比较分析。
根据表 1,假设伪峰数为 1个,以每步 0.5°在-90°~+90°空域进行搜索,分别对阵列数为 15和30的情况下,不同目标数目时采用降维子空间算法在DOA搜索过程中运算量减少的百分比进行了分析,结果如图3和图4所示。
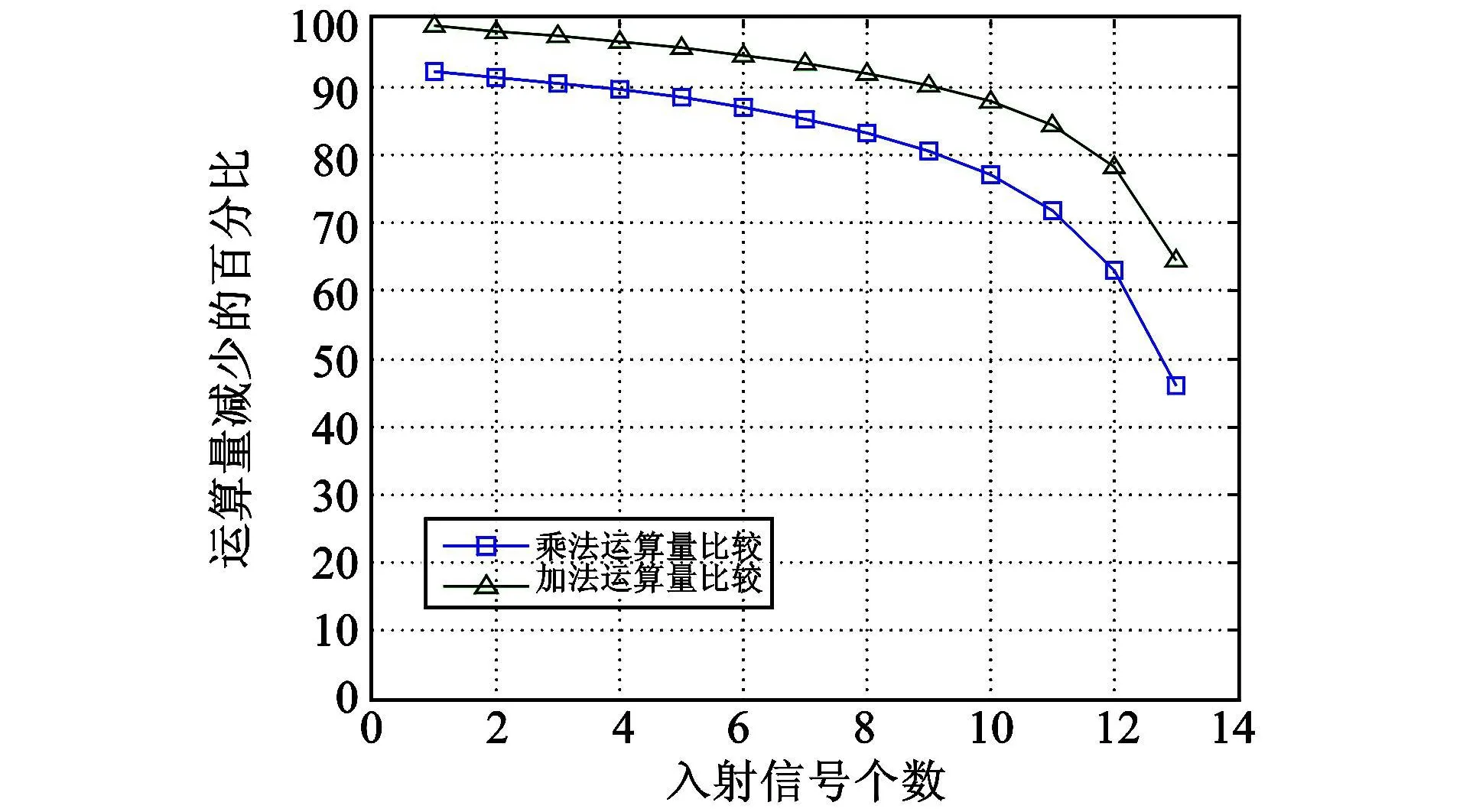
图3 阵列数为15时的运算量比较Fig.3 Comparison of computational complexity in the case of 15 elements
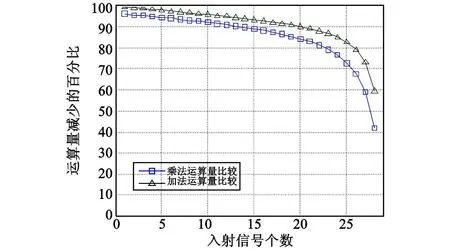
图4 阵列数为30时的运算量比较Fig.4 Comparison of computational complexity in the case of 30 elements
从图3和图4可以看出:尽管降维子空间搜索算法需要对初步估计结果进行校正,总的来看该算法所能够节省的运算量仍然是相当可观的,而且算法最终的精度没有任何损失。
5 结论
综上所述,本文所提出的基于降维子空间搜索算法先利用降维的噪声子空间进行DOA粗略估计,使得MUSIC搜索的运算量大大减小,然后利用最大噪声子空间对估计结果进行修正,保证了MUSIC算法的精度不受损失;性能分析和数值仿真验证了该算法的有效,从而使MUSIC算法更具实用性。
[1]于红旗,黄知涛,周一宇,等.一种不需要特征值分解的ESPRIT方法[J].信号处理,2008,6(24):357-360.YU Hongqi,HUANG Zhitao,ZHOU Yiyu,et al.An improved ESPRIT algorithm without eigenvalues decomposition[J].Signal Processing,2008,6(24):357-360.
[2]于红旗,刘章孟,黄知涛,等.基于快速子空间分解的宽带非相干DOA估计快速算法[J].电子对抗,2008(2):16-20.YU Hongqi,LIU Zhangmeng,HUANG Zhitao,et al.Fast wideband incoherent signal subspace DOA estimation method based on fast subspace decomposition[J].Electronic Warfare,2008(2):16-20.
[3]Mohammed A Hasan.Fast rational approximation algorithms of signal and noise[J].Proceedings of the ISSPA'2001(1):124-127.
[4]黄磊,吴顺君,张林让,等.快速子空间分解方法及其维数的快速估计[J].电子学报,2005,6(33):977-981.HUANG Lei,WU Shunjun,ZHANG Linrang,et al.A Fast Method for Subspace Decomposition and Its Dimension Estimation[J].Acta Electronica Sinica,2005,6(33):977-981.
[5]马洪,杨琳琳,黎英云.二维快速子空间DOA估计算法[J].华中科技大学学报(自然科学版),2008(4):20-23.MA Hong,YANG Linlin,LI Yingyun.A fast subspace algorithm for two-dimensional DOA estimation[J].Journal of Huazhong University of Science and Technology(Nature Science Edition),2008(4):20-23.
[6]Paine A S,Malvern QinetiQ.Fast MUSIC for large 2-D element digitized phased array radar[C]//Proceedings of the international radar conference2003.Adelaide Australia:IEEE,2003:200-205.
[7]CUI Weiwei,CAO Zhigang.Fast Source Location Method Using Anti-reverberant Searching Space Pre-estimation[C]//TENCON 2006,2006 IEEE Region 10 Conference.Hongkang:IEEE,2006:1-4.
[8]蒋毅,古天祥.基于有限域搜索的M USIC法快速频率估计[J].仪器仪表学报,2006,11(27):1 526-1 528.JIANG Yi,GU Tianxiang.Quick frequency estimation based on MUSIC algorithm[J].Chinese Journal of Scientific Instrument,2006,11(27):1 526-1 528.
[9]Schmidt R O.Multipleemitter location and signal parameter estimation[J].IEEE Trans on AP,1986,34(3):276-280.
