对称相关用于直升机声信号特征提取

徐桂芳,高 勇

(1.四川大学电子信息学院,四川成都 610065;2.四川大学锦江学院电子信息工程系,四川彭山 620860)

0 引言

为了解决超低空飞行或悬停直升机目标[1]的探测问题,本文采用被动声探测技术,即利用直升机辐射的噪声来探测直升机目标[2],其研究热点就是利用被动声信号处理技术来识别直升机目标,目标识别的关键在于特征提取。目前,特征提取的方法有AR模型、过零率、快速傅里叶变换(FFT)和子空间分解法[3-4],以及近来提出的谱估计[5]等。

由于直升机的飞行环境相当复杂,传感器接收到的直升机声信号会混有与信号不相关的随机噪声。尽管谱法可以加强低频分量,抑制高斯白噪声[5],但对于信号中混有的不相关随机噪声,消噪效果仍不是很理想。为此,本文结合直升机声信号的飞行环境和频域特性,提出将对称相关函数法和MUSIC算法相结合用于直升机声目标特征提取。

1 理论基础

1.1 直升机声信号频域特性分析

通常直升机有两个旋翼[3],即直升机的主旋翼和尾旋翼。当直升机作变速飞行时,这两个旋翼的旋转速度不变,即使悬浮在空中时也是如此。对于同一型号的直升机,旋翼的1个叶片通过频率称为BPF(Blade Passing Frequency),其值是不变的,并且等于旋翼的叶片数乘以旋翼的旋转速度。一般情况下,主旋翼的BPF用 fm来表示,尾旋翼的BPF用ft来表示。图1为某一直升机声信号的功率谱,由图1可见:直升机的频谱特征具有典型的线谱特性,其信号频谱特性主要集中在0～300 Hz的低频段内。图1中第1个谱峰是 fm产生的,它对应的频率称为直升机的基频,其余谱峰均是 fm与ft的谐波频率。不同型号的直升机,其基频不同。所以,对直升机信号而言,fm与ft以及它们相应的谐波频率是非常重要的目标特征,需要提取和保留。

图1 直升机声信号功率谱图Fig.1 Power spectrum

从上面的分析,可以近似认为直升机声信号为窄带信号,并且具有线谱特征,这些线谱所对应的谐波频率是识别直升机目标的重要特征,将谐波频率和其他特征相结合可以对直升机声目标进行识别。

1.2 对称相关函数的消噪机理

对称相关函数[6]源于应用较广泛的时-频分析——Wigner-Ville Distribution(WVD)的特例。

设x(t)为实函数,x(t)在t时刻的对称相关函数Wx(t)为:

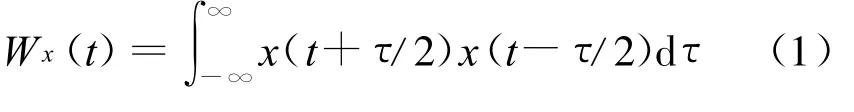
[6]可知:实函数 x(t)的对称相关函数Wx(t)也就是它的WVD在其零频处的值;谐波信号的对称相关函数仍为谐波信号,谐波分量的数目与原信号相同,只是频率、相位增加为原来的2倍。这一点与传统的相关函数有所区别。

设x(t)为实周期信号,周期为T。令

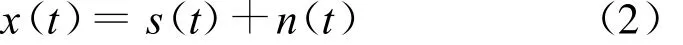
式中,s(t)为有用信号,n(t)是随机噪声,s(t)与n(t)相互独立。

x(t)在t时刻的对称相关函数[7]Wx(t)为:

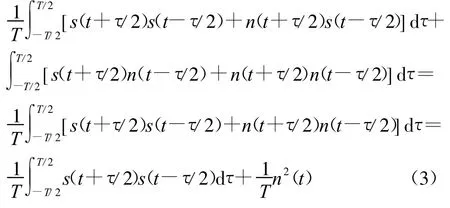
从式(3)知,T取得越长,Wx(t)在t点所受噪声的影响就越小(最后一项),Wx(t)越近似Ws(t)(其中Wx(t)为含噪信号的对称相关函数,Ws(t)为有用信号的对称相关函数),对噪声的抑制能力就越强,这就是对称相关函数消噪机理。而传统相关函数不具备这一优点,始终存在着噪声项,与T的长短无关。

由此可见,对称相关函数法是一种有效的噪声抵消方法,可以包含原信号的所有信息,并且抵消平稳随机过程中与信号不相关的加性随机噪声。

1.3 子空间分解与MUSIC算法

子空间分解方法就是用信号或噪声子空间进行低秩信息的提取。对直升机声信号的特征提取而言,就是在宽带噪声中提取窄带线谱信号的过程。

子空间分解的概念见参考文献[8]。基于子空间分解的谐波频率提取的算法很多,最为著名的是MUSIC算法[3],该算法具有比较高的频率分辨率和良好的抗噪声性能。所以,本文采用此算法。

2 对称相关函数和MUSIC算法相结合的声信号特征提取方法原理

研究表明:直升机辐射噪声的能量主要集中在0～300 Hz的频段上,是由宽带谱加上一系列的低频线谱成分组成的[9-10]。不同类型的直升机,其线谱成分是有差异的(主要体现在特征频率不同)。因此,低频线谱是识别直升机种类的重要特征。但在战场上,由于背景噪声的干扰较强,低频线谱成分经常被背景噪声所淹没,这给线谱特征的提取带来了一定困难。

由前面的讨论可知,对称相关函数法是一种有效的噪声抵消方法,不论噪声类型,只要其不同时刻相互独立,且与信号互不相关,则从理论上即可抵消噪声,保留信号项。信号的对称相关函数的谐波频率是原信号谐波频率的2倍,且谐波数目和原信号相同。而直升机声信号具有谐波特性,因此,用MUSIC算法提取的直升机声信号对称相关函数的谐波频率除以2,就得到直升机声信号的谐波频率。

不难看出:对称相关函数法和MUSIC算法相结合,可以在准确提取直升机声信号谐波频率分量的同时,具有抑制环境噪声和加强低频分量的特性,这就使得它比其他分析方法更具优越性。

3 仿真实验

为检验基于对称相关函数法和MUSIC算法的直升机声目标特征提取的实际应用效果,这里给出一个提取直升机谐波频率值的仿真应用实例。

实际测试中,某些类型的直升机只能测出旋翼噪声,某些类型的直升机能同时测出旋翼和尾桨噪声。旋翼噪声基频在20 Hz左右,而尾桨噪声基频在50 Hz以上[11],二者有较大差别。

实验数据来自于4组实测的直升机声信号数据,数据1和数据2为“米X”的声信号数据,数据3和数据4为“直X”的声信号数据。这些直升机声信号由计算机以44 100 Hz的频率进行采样。在本文中,通过预滤波后按1 024 Hz频率作进一步采样。计算时从每组数据中抽取出1 024个样本点,即 N=1 024。先对每组数据求各自的对称相关函数,再用MUSIC算法分别对每组数据的对称相关函数进行特征提取。

因采样频率为1 024 Hz,依采样定理,分析频率为512 Hz。由于直升机声信号的特征主要集中在300 Hz以下,MUSIC算法中的频率值范围取为0～250 Hz即可,步长Δf=0.5 Hz。为检验上述方法的性能,在实验中将其与维谱以及快速傅里叶变换(FFT)进行了比较。

图2 数据 1仿真结果Fig.2 Simulation of data 1

图3 数据 2仿真结果Fig.3 Simulation of data 2

图4 数据 3仿真结果Fig.4 Simulation of data 3

图5 数据 4仿真结果Fig.5 Simulation of data 4

图2 —图5分别为4组数据的仿真结果。各图中,图(a)为快速傅里叶变换,图(b)为谱估计,

图(c)为本文所述方法。可以看出:对称相关函数和MUSIC算法相结合用于分析直升机声信号的频率特性具有良好的效果。二者都能抑制背景噪声干扰,突出谱峰位置,并且能反映出谱峰间的二次相位耦合关系。它们的性能比一般的功率谱估计要好。

表1列出了用本文所述方法求出的直升机声信号的谐波频率值。

表1 实验中提取的直升机声信号谐波频率值Tab.1 Harmonic f requencies of helicopter acoustic signal Hz

表1列出了实验中提取的直升机声信号谐波频率值。可以看出:“米X”(数据1和数据2)包含主旋翼噪声(基频 f m为17.5 Hz,f m1、f m2、f m3分别为2次谐波、3次谐波和4次谐波)和尾旋翼噪声(基频f t为61.5 Hz,f t1为2次谐波),而“直X”(数据3和数据4)只包含主旋翼噪声(基频 fm为25.5 Hz,f m1、f m2、f m3分别为 2次谐波、3次谐波和 4次谐波)。两种直升机的特征矢量有很大差异,这表明用本文所述方法进行特征提取是合理的,用之识别直升机种类具有优越性。

4 结论

与传统的直升机声信号特征提取方法相比,本文将对称相关函数用于直升机声信号的特征提取,提出了将对称相关函数法和MUSIC算法相结合的直升机声目标特征提取新方法。用MUSIC算法提取直升机声信号的对称相关函数的谐波频率,从而可以得到直升机声信号的谐波频率,将其作为目标特征。而对称相关函数可以对探测到的直升机声信号进行降噪,并保留直升机声信号谐波分量的数目。由实验结果可以看出:将对称相关函数法用于直升机声目标特征提取可以在很大程度上抑制噪声,突出谱峰位置,准确地体现直升机声信号的谐波特性。

参考文献:

[1]张军,赵洪钟,付强,等.悬停直升机的识别[J].系统工程与电子技术,2002,24(2):6-9.ZHANG Jun,ZHAO Hongzhong,FU Qiang,et al.Recognition of ahovering helicopter[J].Systems Engineering and Electronics,2002,24(2):6-9.

[2]Yoon Sang Ho,Kim Byungwook,Kim Young Soo.Helicopter classification using time-frequency analysis[J].E-lectronics Letters,2003,36(10):1 871-1 872.

[3]周忠来,施聚生,栗苹,等.子空间分解法在声目标特征提取中的应用[J].北京理工大学学报,1999,19(6):750-753.ZHOU Zhonglai,SHI Junsheng,LI Ping,et al.Application of subspace decomposition in feature extraction of acoustic targets[J].Transactions of Beijing Institute of Technology,1999,19(6):750-753.

[4]周忠来,施聚生,栗苹,等.基于SVD-TLS的AR 谱估计方法在声目标识别中的应用[J].探测与控制学报,2000,22(1):56-60.ZHOU Zhonglai,SHI Jusheng,LI Ping,et al.The application of AR spectrum estimating method based on SVDTLS in acoustic target identification[J].Journal of Detection&Control,2000,22(1):56-60.

[6]樊养余,陶宝祺,熊克,等.基于对称相关函法的谐波信号重构[J].信号处理,2001,17(5):400-405.FAN Yangyu,TAO Baoqi,XIONG Ke,et al.Harmonic signal reconstruction by the symmetrical correlation function from additive noise[J].Signal Processing,2001,17(5):400-405.

[7]樊养余,陶宝祺,熊克,等.加性噪声抵消的对称相关函数法[J].数据采集与处理,2001,16(3):343-347.FAN Yangyu,TAO Baoqi,XIONG Ke,et al.Symmetrical correlation function used to suppress additive noise[J].Journal of Data Acquisition&Processing,2001,16(3):343-347.

[8]Schmidt R O.Multiple emitter location and signal parameter estimation[J].IEEE Trans Antennas Propagat,1986(34):276-280.

[9]祝龙石,张清泰,刘紫英.直升机噪声理论分析[J].制导与引信,1994(4):10-15.ZHU Longshi,ZHANG Qingtai,LIU Ziying.Theoretical analysis on helicopter noise[J].Guidance&Fuze,1994(4):10-15.

[10]祝龙石,庄志洪,张清泰,等.战场声目标噪声特性分析[J].探测与控制学报(原现代引信),1996(2):57-61.

[11]王昭.小基阵高精度声测被动定向技术研究[D].西安:西北工业大学航海学院,1999.