基于分层结构的复杂多发箔条云团散射模型

崔宏林,卢永革,周 平

(1.中国人民解放军92941部队,辽宁葫芦岛 125000;2.目标与环境电磁散射辐射国防科技重点实验室,北京 100854;3.中国传媒大学通讯工程系,北京 100024)

0 引言

箔条是使用最早、应用最为广泛的无源干扰手段之一,在现代战争中占据相当重要的地位,是各种飞机、舰船等运动目标必备的自卫干扰设备之一,因此研究箔条云团的电磁散射特性显得十分重要[1-2]。如今,对单根箔条电磁特性的研究理论已经十分成熟,但是在计算整个箔条云团的雷达散射截面(RCS)时,由于箔条云团中包含箔条的数量非常多,如果采用传统的矢量辐射输运理论解[3],计算机的运算量将会非常庞大,难以适应实时分析的需要。以A.R.Sterns为代表的半解析法[4-6],采用宏观小微观大的思想把云团划分成一定数量的小单元,使运算更加简洁,但是这种方法多数没有考虑单元之间的耦合场特性,计算精度有限。在本文中,我们把箔条云按照一定的规则划分成箔条云单元体来建立箔条云数学模型,提出了基于分层结构的复杂多发箔条云团散射模型。

1 箔条云团的“层-角-角”结构

箔条云团本身相对雷达来说是一个处于一定位置的椭球体,如图1所示[2]。根据计算精度需要,这里按照“层-角-角”的剖分规则,将箔条云团分割成若干箔条单元体。

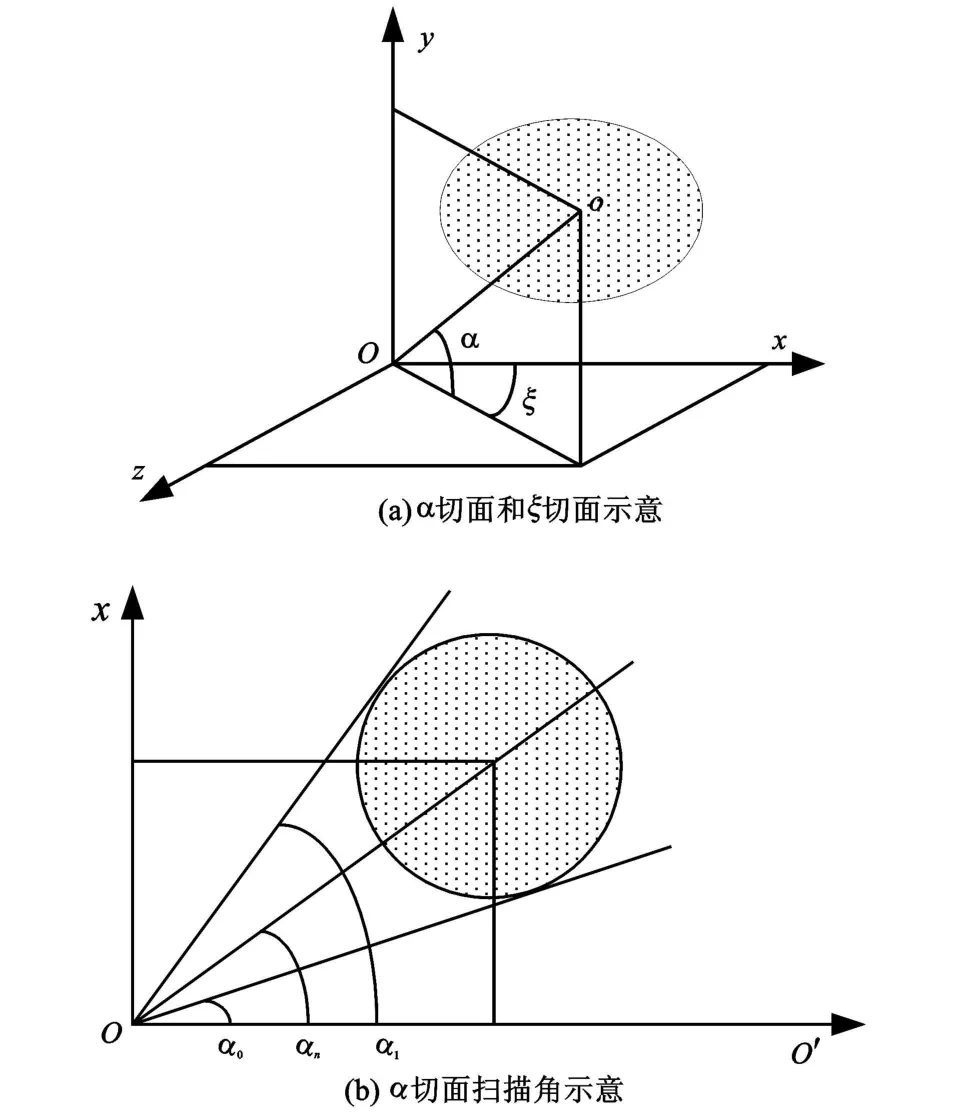
图1 箔条云团的“层-角-角”剖分示意Fig.1 Illustrations of"layer-Kok-Kok"structure of the chaff clouds

箔条云团的形状有可能是椭球形或者球形,在对其进行层划分时,要把其形状等效为以箔条云团的中心点为中心,最大半径为半径的球体来进行划分。在外部坐标系中,要首先计算箔条云团的中心距原点的距离和箔条云团的最大半径,以便于判断雷达和箔条云团的相对位置。在对箔条云团进行层划分时,要按雷达在云团内部和外部两种情况进行划分。

当有多发箔条云团存在时,要对云团逐一划分,分别得出对它们进行划分的最初和最终半径。以雷达在云团外部的情况为例,对所有的箔条云的通用公式[2]为:

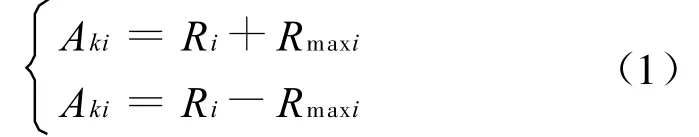
从其中选择使用

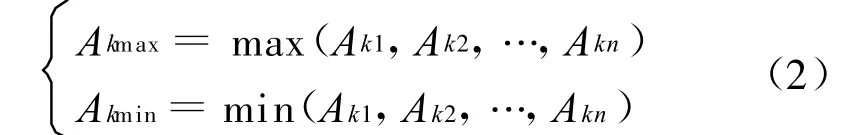
最后根据设定的划分层数 N来求出所划分的箔条云球层的厚度,即每一个层状体的行距

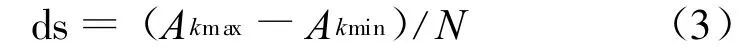
在对箔条云进行角划分时,我们采用的是空间极坐标的两个角度进行划分的。为了方便计算,我们分别建立两个切面,α切面和ξ切面。对于箔条云团处于一般位置时,取的是过箔条云团中心和x轴的平面作为α切面,如图1(b)所示。在α切面中扫描角α为x轴正半轴与雷达和箔条云团中心连线之间的夹角;而ξ切面我们取的是过箔条云团中心和xOz面垂直的平面,在对箔条云团进行ξ切面内的ξ角划分时,为了方便起见,先将这个平面投影到yOz平面上再进行划分,那么ξ角为在yOz面内,是从y轴正半轴开始向z轴正半轴旋转所转过的角度。它们的取值范围分别为 :α∈ [0,π],ξ∈ [-π,π] 。

在这两个切面中对箔条云团进行划分时,需首先确定箔条云团和雷达的位置属于上述三种场合中的哪种场合,然后再确定此种场合下雷达的扫描区间(即α和ξ的最大和最小值之间的区域)和扫描宽度(即每次扫描转过的角度,此角度要根据所设定的分层步数来确定),最后同上述层状划分的规则一致,先后对α和ξ切面上的箔条云团进行角度划分。在完成了对箔条云团的角划分后,对箔条云团的整体划分也已完成,箔条云团已经被划分为逐层的扇形单元体。

2 基于分层结构的云团散射模型

当箔条云处于大数量高密度时,计算箔条之间相互影响的作用是相当重要的,因为这时箔条云的相邻箔条之间的距离很小。箔条之间相互影响的关系可以按下面经验公式计算。

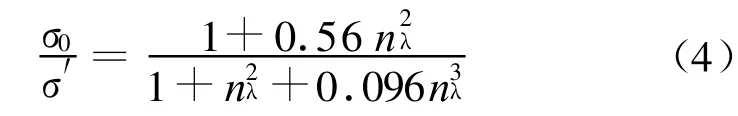
式中,σ0为单独存在的箔条RCS,σ′为箔条云团内的箔条RCS,nλ是箔条体积内的箔条半波线段数量,nλ=ρ◦2λ2◦l,l是箔条长度,ρ为箔条云的密度。

根据式(4)定义相互作用系数

同时,当箔条云团的密度较大时还需要考虑电磁波在箔条云团内传输时的信号衰减,即遮挡阴影效应。经过箔条云团衰减后的出射功率可以表示为:

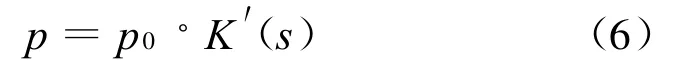
式中,p0为进入箔条云团时的入射功率,p为通过箔条云团阴影厚度为s的路径后的出射功率。K′(s)为阴影系数,分析单元体所积聚的不同密度的箔条,其自身的阴影效果可以用下面的阴影系数表示。

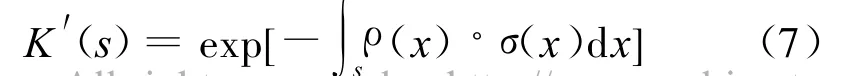
式中,ρ(x)和σ(x)分别是x处箔条层内的密度和有效散射截面。

因此,对于某一箔条单元体所产生的雷达散射截面表示为

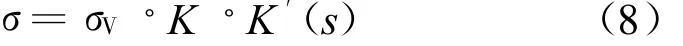
式中,σV是箔条云团单元体内所有箔条RCS的总和。单个箔条的RCS可由文献[6]的方法获得,这里不再累述。

计算出每个箔条单元体的雷达散射截面,将所得单元体的RCS结果按照分割时的规律逐一叠加,考虑单元体互相作用系数和阴影效应,即可得到整个箔条云团的RCS。

3 散射模型的验证

为保证箔条云团单元体RCS计算的准确性,首先计算了单箔条的雷达散射截面,它是由箔条长度决定的。在条件l/λ≤5时,可采用如图2所示的有效雷达散射截面的数值,该图反映了箔条有效雷达散射截面与相对长度的关系。在l/λ≥5时可以近似计算出此类的关系并且可以使用下面的公式计算

式中,σm=2πal2/λ,Ux(ka)是系数,它反映了有效雷达散射截面与箔条直径的关系,其关系式为:

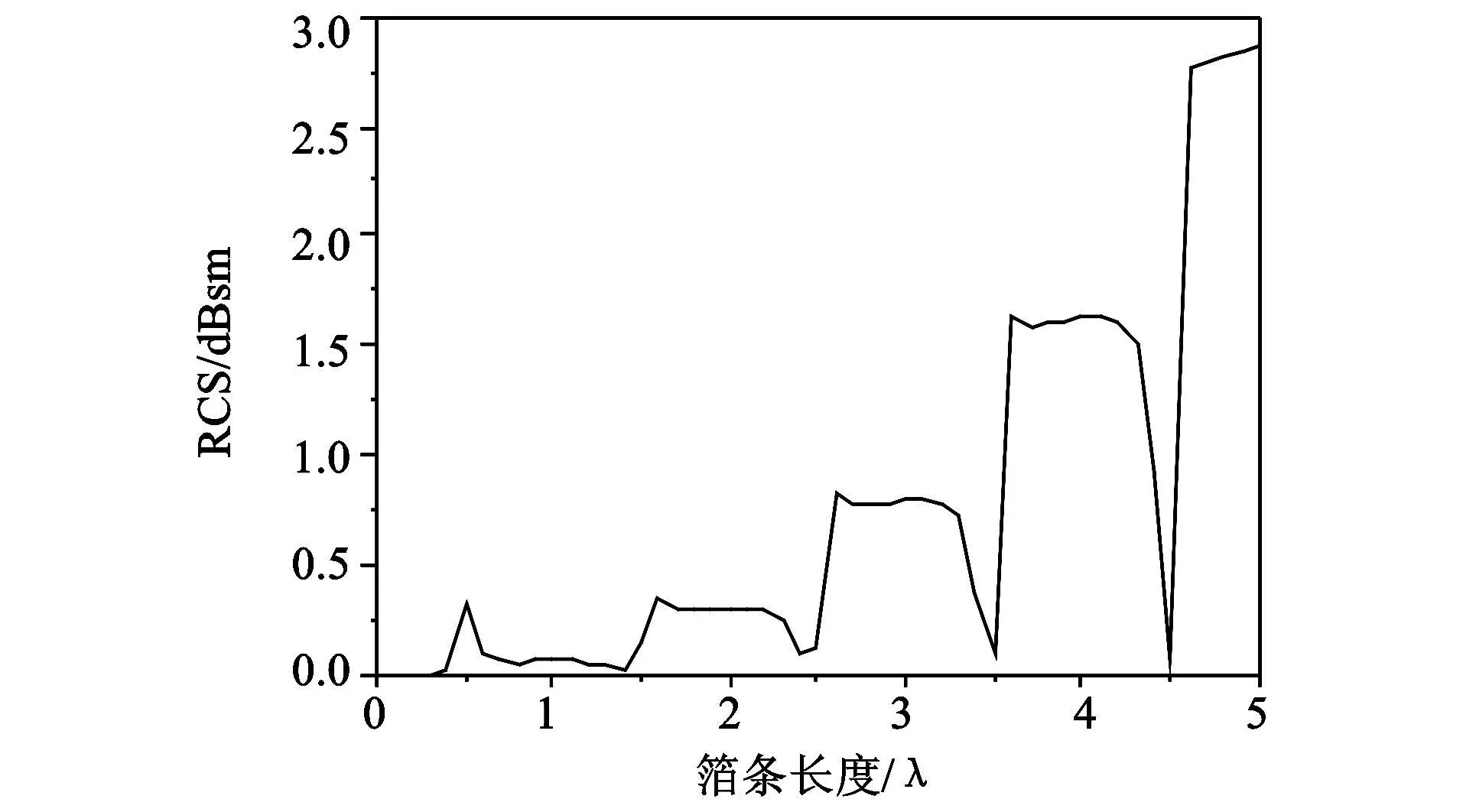
图2 箔条有效雷达散射面与相对长度的关系Fig.2 Relation between the effective RCS and relative length of the chaff

在此基础上,计算了运动雷达在一个固定箔条云团下方匀速飞过时箔条云团的雷达散射截面和多普勒频率特性。假设椭球形箔条云团在外部坐标系下的坐标为(30,15,0),长轴半径为20 m,短轴半径为10 m,包含箔条数为50万根,箔条长度为0.015 m,箔条直径为0.000 5 m,所有箔条在箔条云团中是均匀分布的。另外,假设一个运动雷达以1 000 m/s的速度在箔条云团下方匀速飞过,它从外部坐标系原点出发,沿 x轴直线飞行,其入射波仰角为60°,扫描宽度为 10°,方位角为 0°,扫描宽度为 180°,发射信号为连续波信号,波长0.03 m。我们设置对箔条云团的层面划分为100层,切面划分均为20个角间距进行划分。计算结果如图3所示。

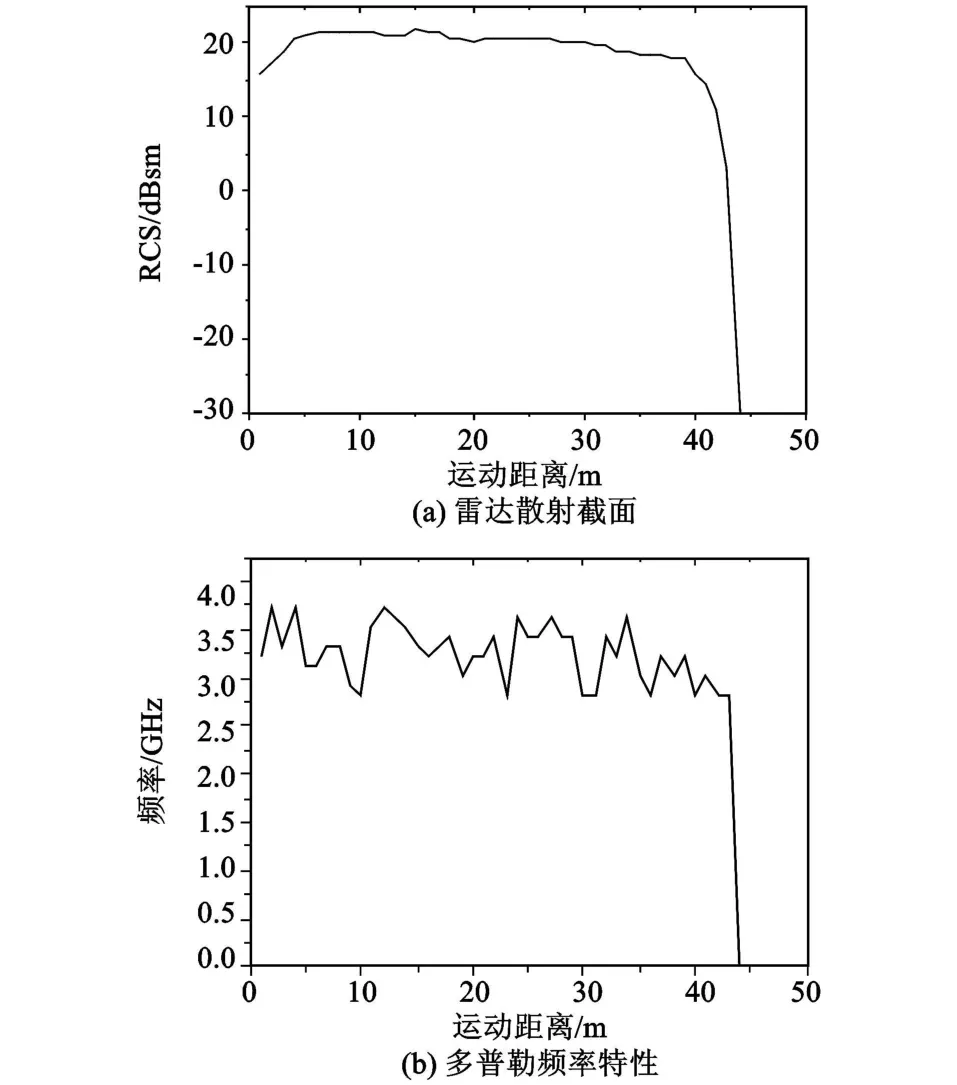
图3 运动雷达探测箔条云团的散射特性Fig.3 Scattering character of the chaff clouds detecting by moving radar

从图3可知:运动雷达飞行距离在0～40 m时,RCS值在15 dBsm附近上下波动,说明箔条云团已经全部进入雷达的探测范围之内;运动雷达飞行距离在41～44 m时,探测到的RCS值逐渐减小,由10 dBsm下降到-30 dBsm,说明此时箔条云团逐渐到了运动雷达探测范围之外;运动雷达飞行距离在45～50 m时,探测到的RCS值小于-30 dBsm,说明测试箔条云团已全部在运动雷达的探测范围之外。

值得一提的是,由于采用了“层-角-角”划分的箔条单元体迭代散射模型,每个运动位置的模拟计算时间不超过3 s,整个运动距离的计算时间不超过150 s,效率远远高于文献[3]的矢量辐射输运分析模型,较好地满足了实时分析模拟的需要,同时计算的精度也得到较大提高。

图4给出了同样运动雷达条件下不同模拟条件对箔条云团雷达散射截面的影响。

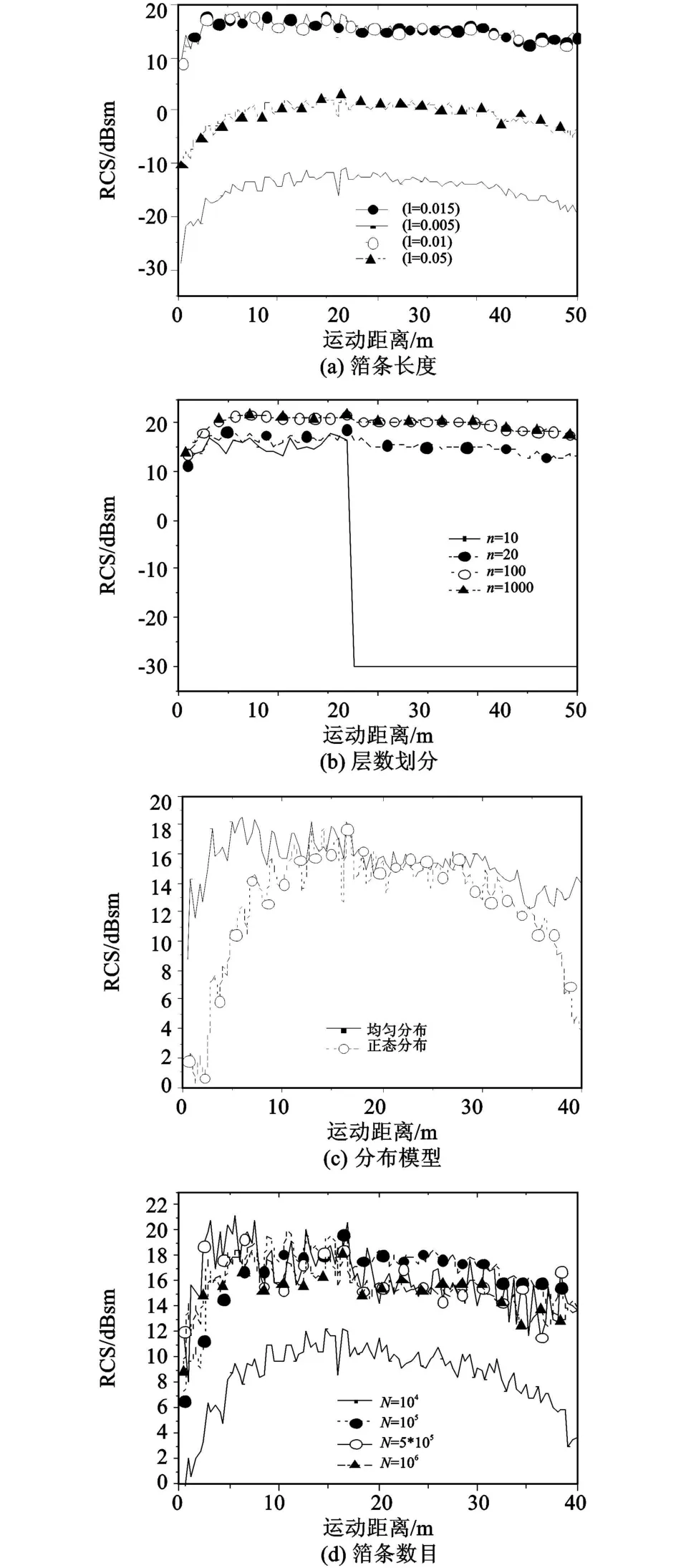
图4 不同模拟条件对云团散射截面的影响Fig.4 The effect of chaff clouds RCS f rom different simulating conditions

图4 (a)为不同箔条长度、图4(b)为不同的层数划分、图4(c)为不同云团分布模型、图4(d)为不同箔条数目对箔条云团雷达散射截面计算结果的影响。从图4(a)中可以看出:波长不同时测得的RCS结果变化很大,其中RCS值最大的一组为l=0.015 m,此时箔条长度等于半个波长,电磁波达到谐振状态,云团的干扰效果最为明显。图4(b)—图4(d)均选用此谐振状态下计算,由图4可知,当划分层数为10时,出现较严重的图形失真情况,而划分100和1 000层时,图形基本吻合;从图中我们还可看出,由于正态分布时,云团外围的箔条数目较少,箔条主要集中在云团的中心区域,所以云团对雷达的影响距离变小;另外,高密度云团能达到较好的干扰效果。

最后,来讨论多发箔条云团的不同排列方式对云团电磁散射特性的影响。计算中分别选取多发水平排列圆形箔条云团和多发正方形排列圆形箔条云团,其中心坐标分别为(30,15,0)、(50,15,0)、(70,15,0)、(90,15,0)、和中心坐标分别为(40,15,0)、(60,15,0)、(40,30,0)、(60,30,0),半径均为 10 m的两种不同排列方式,分别如图5(a)、(b)所示。

图5 多发云团分布几何位置示意Fig.5 Geometry position of several chaff clouds

图6 为两种多发箔条云团分布条件下RCS的计算结果,图6中正方形排列的箔条云团的RCS值基本稳定,而水平排列的箔条云团的RCS值变化较为明显。这是由于在排除了雷达天线扫宽因素的干扰之后,云团自身的遮挡效应所导致的。

图6 不同排列的箔条云团计算结果Fig.6 Computed results of the different arrangement chaff clouds

4 结论

本文提出了一种基于分层结构的复杂多发箔条云团散射模型。这种模型的特点在于它利用了“层-角-角”结构划分和精确单元箔条散射截面的计算方法的优势,并且考虑了箔条单元之间的互相作用系数和阴影效应,因此其计算效率和精度得到显著提高。同时由于该模型可以再现雷达信号反射过程,特别符合弹目交会的实时模拟需要。模型的验证分析表明,可以获得准确的实时分析结果。

[1]李铁,王纬宇,田博.不同密度分布箔条云的单站雷达截面[J].探测与控制学报,2005,27(1):5-8.LI Tie,WANG Weiyu,TIAN Bo.Monostatic RCS of chaff clouds with various density distribution[J].Journal of Detection&Control,2005,27(1):5-8.

[2]陈静.箔条理论和微波技术[M].锦州:电子工业部第53研究所,1997.

[3]张民,吴振森,薛谦忠.大数量高密度圆形箔片云团双站电磁散射特性[J].电子学报,2001,29(3):364-367.ZHANG Min,WU Zhensen,XUE Qianzhong.Study on the bistatic RCS of a great number of dense foil clouds[J].Acta Electronica Sinica,2001,29(3):364-367.

[4]Sterns A R.The use of chaff in space as ajamming device between ground stations and satellites,ADA292577[R].Athens:Air Force inst of Tech Wright-patterson AFB OH School of Engineering,1988

[5]Kownacki S.Screening effect of a chaff cloud[J].IEEE Trans on Aerosp,1967,11:34-37.

[6]Peyton Z,Peeles J.Bastatic radar cross sections of chaff,ADA 133967[R].Gainesville:Florida Univ Gainesville E-lectronic Communications LAB,1983.