纯方位角定位的单步最优观测轨迹算法
2010-08-21权宏伟彭冬亮薛安克
权宏伟,彭冬亮,薛安克
(1.华东理工大学信息科学与工程学院,上海 200237;2.杭州电子科技大学信息与控制研究所,浙江杭州 310037)
0 引言
纯方位角定位与跟踪是信号检测及滤波理论领域内一类较难解决的问题[1-5]。实际观测过程中,目标定位精度不仅受随机观测噪声的影响,而且也与观测平台的运动轨迹有关[6]。为提高目标的定位精度,通常要求观测平台沿某条最优轨迹运动,以保证最后得到的关于目标状态的估计量具有最小的估计误差。观测平台最优轨迹设计是指选取适当的系统优化性能指标,使得在该观测轨迹下得到目标定位精度最高。本文研究的即是如何设计最优观测平台轨迹的问题。
目前,国内外大多数学者都使用Fisher信息矩阵(FIM)作为轨迹优化的性能指标,但在具体算法上对FIM的处理不同。Andrew提出了信息论方法,通过最大化观测量序列的互信息来求取最优观测路径。这种方法实质上等同于最大化FIM的行列式[7]。Passerieux引入信息率的概念,给出了目标在匀速直线运动时的最优观测平台轨迹[8]。上述方法在求取最优观测轨迹时,都加入了一定的限制性条件,如限定观测次数及观测平台终止状态等。同时,将离散的观测位置点处理成连续的观测轨迹曲线,使得算法求取的观测轨迹可能只具有局部最优性。
本文提出了一种实践上易于实现的最优观测平台轨迹算法,即单步最优观测轨迹算法。与文献[8]的方法类似,单步最优观测轨迹算法也以Fisher信息矩阵作为系统的观测性能指标。考虑到各次观测相互独立的条件下,系统总的Fisher信息矩阵等于单次观测的Fisher信息矩阵之和[9],单步最优观测轨迹算法实现了从观测平台初始观测位置开始,在后续每一时刻的观测位置上达到目标的观测性能最优。
1 纯方位角目标运动分析
1.1 系统模型
选取直角坐标系为系统的参考坐标系。设目标与观测平台运动轨迹位于同一坐标平面内。观测平台在k时刻的位置坐标用状态向量[Sx(k),Sy(k)]T表示。平台从当前观测点运动到下一个观测点的方向变量用u(k)表示。从而平台在k+1时刻的位置坐标总可以用k时刻的位置坐标与方向变量u(k)表示。假定观测平台从当前观测位置以常速率V经过时间T运动到下一个观测位置,平台的运动方程为:
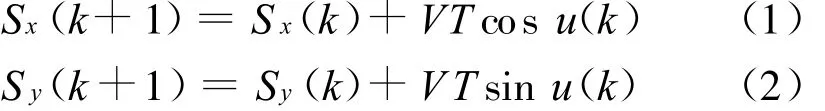
观测平台初始位置已知的条件下,根据式(1)、式(2),平台在任一时刻的位置都可以表示成控制变量序列{u(1),u(2),…,u(k)}的函数。第k次观测的目标与观测平台相对位置如图1所示。

图1 k时刻的目标与观测平台相对位置Fig.1 Relative location of target and observer at time k
设目标的位置状态向量为 η=[Ox,Oy]T。目标的观测方程为:

式中:
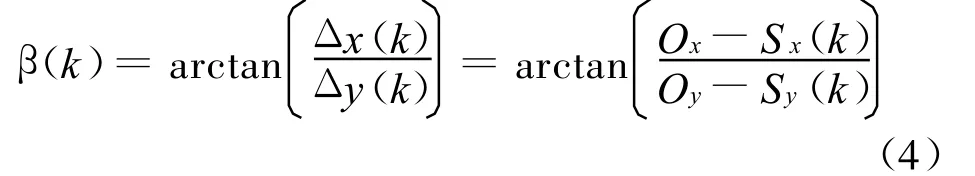
β(k)是k时刻目标相对于观测平台的真实方位角(以正北为参考方向);ω(k)为随机高斯观测噪声,方差为;Z(k)表示实际测量角度。

1.2 Fisher信息矩阵
对于适当的观测噪声,在观测平台正确机动的情况下,可以得到关于目标状态参量的无偏估计量,该估计量的协方差矩阵能够达到Cramer-Rao下限,它等于Fisher信息矩阵的逆。就静止目标而言,N次观测后目标状态参量的Fisher信息矩阵为[9]:

符号E(◦)表示求数学期望。进一步计算可得:

式中:

同理,可求得单次观测的Fisher信息矩阵。第k次观测的Fisher信息矩阵为:
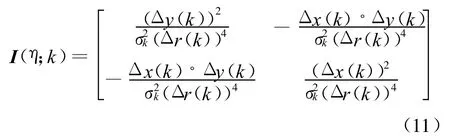
比较式(7)与式(11),显然有:

2 单步最优观测轨迹算法
选取目标状态参量的Fisher信息矩阵为系统的观测性能指标。以第一步控制变量的确定为例来说明单步最优观测轨迹算法。根据1.1节观测平台在初始位置状态已知的假设,由式(7)得到该观测位置上的Fisher信息矩阵 I(η;1)。由式(1)、式(2)可知,观测平台在第2个观测点的状态[Sx(2),Sy(2)]T可以表示成控制变量u(1)的函数。代入式(11)得第2个观测点的Fisher信息矩阵I(η;2)。根据公式(12),当前系统的Fisher信息矩阵为:

因为Fisher信息矩阵是半正定的,根据矩阵分析中的知识可以得到以下结论:Fisher信息矩阵的逆矩阵即误差协方差阵的二次型定义了一个超椭圆,它的n个特征值代表超椭圆的n个半轴。误差协方差矩阵P的1-σ域由下式表示[10]:
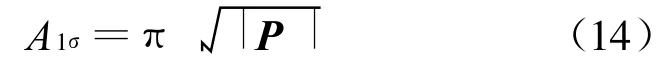
根据Fisher信息矩阵I与误差协方差矩阵P的关系,上式又可写为:

由上式可以看出,1-σ域随信息矩阵行列式的值增大而变小,这也意味着系统关于目标的观测性能越好。对式(13)两边取行列式:

Det(◦)表示求矩阵的行列式。上式右端为系统的性能指标,令:
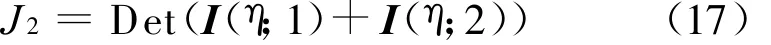
显然J2是控制量u(1)的函数,即。最优控制量是使得系统当前性能指标J 2最大的控制量:
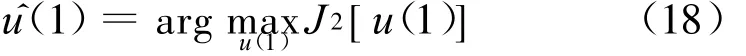
由上式求得最优控制量^u(1),将^u(1)代入式(1)、式(2),得到第2个时刻的最优观测位置坐标及相应观测点上的Fisher信息矩阵。迭代上述算法,可顺序求得第k个时刻的最优观测平台位置坐标。这k个有序的观测点位置坐标构成了最优观测平台轨迹。单步最优轨迹算法流程如图2所示。

图2 单步最优轨迹算法流程图Fig.2 Flow chart of single-step optimal trajectory algorithm
单步最优轨迹算法是一个迭代求解观测平台最优运动轨迹的算法。每进行一次迭代,可求得观测平台的下一个最优观测位置点。理论上,该算法不受终止条件的限制,在求解最优轨迹的过程中,一般把观测平台接近目标位置作为算法的结束条件,当然,也可以通过设定观测次数来结束算法。
3 仿真及结果分析
算法采用Matlab仿真平台进行仿真。取目标的实际位置为(1 200 m,1 200 m)。观测平台初始位置位于坐标原点,速率V=5 m/s,观测周期T=1 s。单步最优观测平台轨迹如图3所示。
由图3可见,采用单步最优观测轨迹算法得到的轨迹有两条。这是由于在第一个观测点上存在两个最优控制量^u(1)的缘故,这可由图4进一步说明。图4给出了性能指标J 2[u(1)]与控制变量u(1)之间的关系。
从图4中不难看出,使得性能指标J 2[u(1)]达到最大值的控制变量u(1)有两个,并且这两个最优控制量关于目标与观测平台初始位置的连线是对称的。因而,算法得到的两条轨迹也关于该连线对称。

图3 单步最优观测平台轨迹Fig.3 Single-step optimal observer trajectories

图4 控制变量u(1)与性能指标J 2[u(1)]的关系Fig.4 Relationships of control variable u(1)and Performance Index J 2[u(1)]
4 结论
本文提出了一种在实践上易于实现的最优观测平台轨迹算法,即单步最优观测轨迹算法。该算法实现了从观测平台的初始观测位置开始,在后续每一时刻的观测位置上达到目标的观测性能最优。仿真表明,算法获得的单步最优观测平台轨迹是有效的。需要指出的是,本文仅研究了目标静止状态下观测平台的单步最优轨迹,对于目标作匀速直线运动或其他运动的情况,还需作进一步的研究。此外,对于观测过程中的观测噪声不满足高斯白噪声假设的情况,也有待进一步的分析。
[1]Trémois O,Le Cadre J P.Optimal observer trajectory in bearings-only tracking for maneuvering sources[J].IEE Proc Radar,Sonar Navig,1999,146(1):31-39.
[2]Song T L.Observability of target tracking with bearingonly measurements[J].IEEE Trans.on Aerospace and Electronic Systems,1996,32(4):1 468-1 472.
[3]许志刚.纯方位系统定位与跟踪的观测器最优机动轨迹[J].连云港化工高等专科学校学报,2002,15(1):1-4.XU Zhigang.Optimal observer maneuver for bearings-only localization and tracking[J].Journal of Liangyungang College of Chemical Technology,2002,15(1):1-4.
[4]权宏伟,彭冬亮,薛安克.纯方位角目标运动分析的可观测性研究[J].火力与指挥控制,2009,34(10):43-46.QUAN Hongwei,PENG Dongliang,XUE Anke.Observability of Bearings-only target motion analysis,Fire Control&Command Control,2009,34(10):43-46.
[5]Fogel E,Gavish M.Nth-order dynamics target observability from angle measurements[J].IEEE Trans on Aerospace and Electronic Systems,1988,24(3):305-308.
[6]Ghassemi F,Krishnamurthy V.A method for constructing the observer trajectory in bearings-only tracking of targets with a Markovian model[C]//Proc of the2005 IEEE Int Conf on Information Acquisition.USA:IEEE,2005:1-5.
[7]Logothetis A,Isaksson A,Evans R J.An information theoretic approach to observer path design for bearings-only tracking[C]//Proc of the 36th conf on Decision&Control.USA:IEEE,1997:3 132-3 137.
[8]Passerieux J M,Van Cappel D.Optimal observer maneuver for bearings-only tracking[J].IEEE Trans on Aerospace and Electronic Systems,1998,34(3):777-788.
[9]Bar-Shalom Y,Li X R,Kirubarajan T.Estimation with applications to tracking and navigation[M].New York:Academic Press,2001.
[10]Hammel S E.Optimal observer motion for bearings-only localization and tracking[D].RI,USA:University of Rhode Island,1988.
