随机环境下铁路军事运输保障作战模拟决策方法研究
2010-08-21李常双胡建军周飞飞赵喜庆军事交通学院天津300161LIChangshuangHUJianjunZHOUFeifeiZHAOXiqingAcademyofMilitaryTransportationTianjin300161China
李常双,胡建军,周飞飞,赵喜庆(军事交通学院,天津300161)LI Chang-shuang,HU Jian-jun,ZHOU Fei-fei,ZHAO Xi-qing(Academy of Military Transportation,Tianjin 300161,China)
随机环境下铁路军事运输保障作战模拟决策方法研究
Study on Decision-making in Simulation of Military Railway Transport Guarantee under Stochastic Condition
李常双,胡建军,周飞飞,赵喜庆(军事交通学院,天津300161)
LI Chang-shuang,HU Jian-jun,ZHOU Fei-fei,ZHAO Xi-qing(Academy of Military Transportation,Tianjin 300161,China)
以博弈论为基础,以战时铁路军事运输保障为背景,建立了红蓝双方动态非接触对抗的决策模型;针对战时铁路军事运输保障决策中的随机问题,提出了天气影响因子和随机影响因子,反映战场随机环境对红蓝双方的影响,并建立了随机期望值决策模型。通过模拟,合理设置战场随机状态,客观分析输送过程,为战时铁路军事运输保障决策提供有力的决策支持,方法直观、有效,具有很好的应用前景。
铁路军事运输保障;随机环境;决策;博弈论
Abstract:This paper on the basis of game theory,and taking the military railway transport guarantee on war time as the background,we established an opposed dynamic and non-contact decision-making model.Aiming at the problems in military decision-making under stochastic condition in uncertainty, we put forward the factors of weather and stochastic influence, which reflects the influence of stochastic condition on the red and the blue,and establishes stochastic opposed decisionmaking models in anticipant value and in correlative chance way farther.It can be seen from the simulating results that the models can dispose the stochastic status in battlefield reasonably,analyse the transport result impersonally,and offer a powerful decision-making sustaining for military command and control.The proposed method is very practical and effective, and has a good applying future.
Key words:military railway transport guarantee;stochastic condition;decision-making;game theory
Study on Decision-making in Simulation of Military Railway Transport Guarantee under Stochastic Condition
0 引言
作战指挥决策是为完成和依据各种条件而进行的选择作战目标和选择实现目标行动策略的思维活动。其中,每项指挥活动都是一个不确定性的动态过程,最终的决策效果取决于动态过程中每一决策阶段的局势都要朝着有利于自己的方向发展。信息化条件下的战争,战场空间增大,交战空间减小,前后方的概念日益模糊,因此,铁路军事运输始终在高强度的对抗环境中进行。此外,由于信息化战争的复杂性、隐蔽性、欺骗性、对抗性越来越凸显,大量的决策可能在不确定环境中进行,因此,研究不确定条件下的动态指挥决策优化方法及其应用显得非常重要。针对以上问题,本文以战时铁路运输保障非接触对抗环境为背景,在一般博弈论的基础上,建立了随机环境下动态决策模型,并进行模拟验证。
1 基本战场想定
设定战时铁路军事运输保障作战模拟的对抗双方为红方机动方(记为Y),蓝方阻挠方(记为B)。红方包含多个列车梯队Yi=(Y1,Y2,…,Ym),主要任务是在蓝方阻挠破坏的情况下选择最优策略,使总延误时间最小;蓝方包含空中打击力量Bj=(B1,B2,…,Bq),主要任务是对红方机动径路上的关键点进行打击以阻挠红方机动;本文模拟的是运输过程中的动态决策方法,因此不考虑装卸载过程。由于战时铁路军事运输对抗环境的特点,机动方与阻挠方没有直接的火力交互,双方的决策收益通过路网空间R=(E,V)反应。
基于动态规划的思想,采用模拟的方法将运输过程按若干时域离散化为K个阶段。红蓝双方及路网的阶段状态空间模型如下:

式1表示阶段k时红方机动与抢修状空间,式2表示k阶段蓝方武器平台状态空间,式3表示路网在阶段k节点与路段状态空间。
2 随机环境下双方决策建模
2.1 随机环境影响因子建模
由于军事运输过程中的复杂性、隐蔽性、欺骗性和对抗性,使得获取信息的难度越来越复杂,大量的决策均在不确定环境中进行。同时,众多的不确定因素对决策的影响是很大的,在众多不确定因素中,一般的,天气因素对铁路运输的影响较小,但在战时军事运输中,对蓝方的空中打击和红方的抢修/抢建影响更为直观和直接。本文考虑将随机环境下的随机因素划分为基于Markov chain的随机天气模型以及影响双方决策收益的随机因素影响因子两种模型,其中,随机因素影响因子模型用以反映情报侦察、战场评估等随机因素的影响。
2.1.1 基于Markov chain的随机天气模型
将输送模拟过程中的天气影响程度分为3级:1级、2级、3级,其中1级最好,3级最差。天气状态更新的时间同样为阶段k的时间步长,共有K个更新周期。设节点i区域Ai处在阶段k的天气状态为ai()k,状态空间为{1,2,3},由于共有N个区域,可知该天气模型是一个有4NK种状态的马尔科夫链。定义pwij(k)为当前阶段天气状态i,下个阶段变为j的转移概率。天气因素对红蓝双方的活动影响通常通过定性分析或以经验值进行估计,很难确定准确的分布函数。本文假设天气影响随机变量ζIa(k)∈(1,+∞)表示阶段k在节点v处天气状态ai(k)对红蓝双方策略收益的影响程度,则天气影响因子χIi(k)=pwij(k)·ζIa(k)。
2.1.2 随机因素影响因子建模
正态分布函数常用于描述众多独立随机因素共同作用下的影响,这里设战场环境下情报状况及战场态势评估等若干随机因素对双方策略收益的综合影响为服从正态分布N( μ,σ)的随机变量ξji(k),其中,μ∈[-1,1],σ∈[0,1]。当μ∈[-1,0]时,表示作战平台受到了随机环境的负面影响,决策收益有所减少;当μ∈[0,1]时,表示作战平台受到了随机环境的正面影响,决策收益有所增强。故,正态分布随机变量ξji(k),i={1,2,…,n},j={1,2}定义为阶段k节点i处随机变量对红蓝双方的影响程度。λji(k)为随机影响因子,表示战场随机影响因子阶段k节点i处对红蓝双方的影响程度,j={1,2}。为了度量其对各作战平台的实际影响,取随机变量的正弦值,将各随机变量产生的影响范围度量在(0,2)之间,有:

2.2 红方决策目标模型
红方的决策目标包含机动决策与抢修/抢建模型,由于加入了随机影响因子,由确定性函数转变为不确定性函数,因此,采用期望值算法[1],将目标函数变为相对确定性的问题。
2.2.1 基于路网可靠性的红方机动模型
石玉峰在文献[2]中提出了基于可靠性的战时随机运输时间的路径优化模型,本文在文献[2]的基础上提出建立随机环境下的机动模型,将问题转化为多阶段离散状态下,求置信水平下,任务完成时间T的悲观值,即T最小值,得出各阶段k所对应的最优机动路径。


其中,T为目标函数,即为输送完成的最小时限,E(T)表示输送完成的期望时间,E( Tij(k))表示通过节点i的路径ij的期望时间,α为T不超过T的置信水平,V为路网的节点集合,χ1i(k),λ1i(k)分别为阶段k时,节点i处影响红方的天气影响因子和随机环境影响因子。
2.2.2 抢修/抢建目标模型

符号说明:
qi(k)表示第k阶段节点i可投入的抢修力量。抢修力量包括人员、器材、机械工具等。
Q总表示整个作战阶段可投入的抢修力量总量。
Q作业面表示节点i受打击后,最大作业面可展开的抢修力量。
q'i(k)表示k阶段节点i可提供的抢修等级,与毁伤等级相对应。
Di(k)表示第k阶段节点i的毁伤等级。
其中,式(4)为目标函数,E( Tij(k))为第k阶段红方抢修/抢建策略下经过路网中节点i的径路期望通过时间;式(5)表示β置信水平下,红方抢修/抢建策略;式(6)中有:抢修弧ij的通过期望时间(抢修收益):

抢建弧ij的通过期望时间(抢建收益):
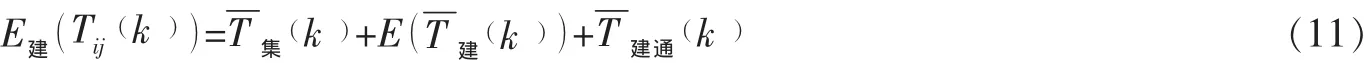
T集(k)表示满足节点i抢修/抢建等级下的保障力量的最小集结时间;E (T修(k ))E (T建(k))分别表示抢修/抢建满足通车条件(平均行驶速度不低于30km/h)的平均期望时间;T(k)T(k)表示通过节点i的平均通过时修通建通间。
式(7)代表抢修力量约束,式(8)代表作业条件约束,式(9)代表抢修等级约束。
2.3 蓝方阻挠模型的建立
由于战时铁路网中影响车流量和通过时间的枢纽站、区间段上的桥梁、隧道等目标易受打击,在路网变形,将这些易受打击破坏的目标转化为节点,进而考虑路网最短路关键点与关键边的问题。文献[3]建立了基于关键点与关键边算法的蓝方阻挠模型,蓝方阻挠模型的实质在于对路网最短路关键点和关键边的选择上,因此路网最短路关键点与关键边的确定是建立模型的基础。在此基础上,引入随机影响因子,采用期望值[1]算法将模型转化为相对确定性问题。将问题转化为γ置信水平下,蓝方选择打击当前路网上影响红方输送的关键节点,使阻挠红方机动时间最大。
模型的假设条件:
①蓝方对节点目标打击后视为目标毁伤程度划分为3级:破坏、严重破坏、摧毁,对应的通过能力分别下降30%、60%、100%;通过能力的下降以通过时间延迟反映。
②路网结构经过变形删除禁止点,并将桥梁等目标表示为节点形式,根据假想敌美军相关军事理论,模拟中只考虑打击路网关键节点以达到作战企图。
建立模型:
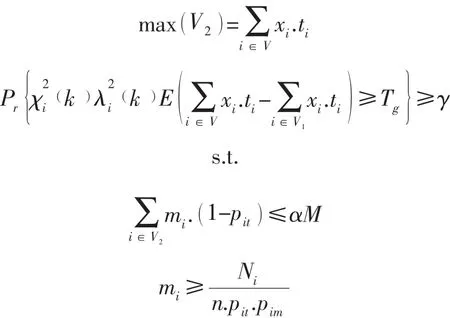

图1 抽象路网
符号定义如下:
V1——原路网最短路集合
V——未被破坏的路网最短路集合
V——蓝方路网目标集合
Xi——通过节点i的列车数
ti——列车通过节点i的平均时间
mi——蓝方投入到第i个打击点的打击力量数
n——蓝方单个打击力量携弹单位
pit——第i个节点的突防概率
pim——蓝方对第i个节点的命中概率
M——蓝方可动用的打击力量
Tg——蓝方预定迟滞时间
Ni——损毁第i个节点所需弹药数
α——蓝方可以接受的损失率
3 模拟与结果分析
3.1 初始条件设定
图1为某路网的抽象图,模拟背景设定为红方开始从s点至t点的一次输送,蓝方集结空中打击力量,阻挠红方输送,对红方当前输送路网上的关键节点进行打击,以达到延迟红方机动、割裂红方态势部署的目的。表1和表2分别表示不同天气条件下蓝方突防概率和命中率,表3表示节点i受蓝方打击后,通过节点i的弧ij满足最低通行条件的最小增加时间的期望值。
模拟共进行了K步,初始参数如表中数值设定,天气状态和随机影响因子采用蒙特卡洛方法进行模拟,取第k阶段为例,红方可选策略:A,当前路网最短路输送;B,等待路径上节点抢修/抢建;C,选择绕行径路;D,选择其他方式输送;蓝方可选策略:E,打击当前路网上的关键节点;F,不打击。
3.2 模拟结果及分析

表1 蓝方突防概率

表2 蓝方对节点i的命中率

表3 通过节点i的最小增加时间
应用Game bit博弈分析工具进行均衡求解。(1)在未考虑天气影响因素和随机环境影响因子的情况下,得到策略均衡点:s*1(k)=(A,A,B,A,A,A,B,A,A),输送径路为s-1-4-t;s*2=(F,F,E,F,F,E,F,F,F)。(2)引入随机影响因子,对决策目标函数进行蒙特卡洛模拟,得到均衡点s*1(k)=(C,A,A,A,D),输送径路s-2-5,变为其他方式输送,s*2(k)=(F,F,E,F,F)。可以看到,随机环境的影响对双方决策的选择均产生了影响,随机影响因子对输送过程产生了不可忽视的影响。
4 结束语
本文以随机环境下的铁路军事运输保障为背景,主要研究了以博弈论为基础的随机环境下的铁路军事运输保障决策问题,建立了动态非直接火力交互对抗的决策模型,并根据战场随机环境对各参战平台的影响,提出了天气影响因子和随机影响因子,建立随机期望值对抗决策模型。模拟结果表明,随机影响因子的设置可以使得铁路军事运输保障作战模拟更加贴近真实环境。建立随机环境下的红蓝双方决策模型,分析战场随机环境对铁路军事运输保障指挥决策的影响,为战时铁路军事运输保障指挥决策提供了有力的辅助决策依据,具有良好的应用前景。
[1]刘宝碇,赵瑞清,王纲.不确定规划及应用[M].北京:清华大学出版社,2003:61-110.
[2]石玉峰.战时随机运输时间路径优化研究[J].系统工程理论与实践,2005(4):133-136.
[3]李常双,李庚.战时铁路军事运输保障模拟蓝方阻挠模型研究[J].军事交通学院学报,2010(5):18-20.
[4]张莉,张安.随机环境下编队协同对地攻防对抗决策方法分析与研究[J].兵工学报,2007(10):1229-1233.
[5]戴玲,夏学知.基于Markov天气模型的流量管理改航策略[J].舰船电子工程,2007(4):57-59.
[6]A.Nilim,L.El Ghaou,i V.Duong,M.Hansen.Trajectory based air traffic management(tb-atm)under weather uncertainty [C]//In Proc.of the Fourth International Air Traffic Management R&D Seminar ATM,Santa Fe,NewMexico,2001:5-6.
F530
A
1002-3100(2010)10-0106-05
2010-07-06
李常双(1984-),男,内蒙古通辽人,军事交通学院研究生管理大队军事运筹学专业硕士研究生,研究方向:作战军交运输保障模拟、车辆路径优化问题。
