广东金马大桥三维地震时程反应研究*

余报楚 邱文亮 余庆军 程晓红 滕启杰

(大连海洋大学土木工程学院1) 大连 116023) (大连理工大学桥梁工程研究所2) 大连 116023)

0 引 言

自1943年M.Biot提出反应谱的概念,以及1948年G.W.Housner提出基于反应谱理论的抗震计算动力法以来[1-5],反应谱分析方法在结构抗震领域得到不断完善与发展,由于反应谱仅能给出结构各振型反应的最大值,而丢失了与最大值有关且对振型组合又非常重要的信息,对大跨结构即使结构是处于线弹性状态,反应谱方法仍不能代替时程分析法.时程分析法目前发展较为成熟[6-7],该方法在计算上不仅能很好地解决多点输入,而且可以考虑结构的非线性、非比例阻尼等,因此通常在大跨度桥梁结构分析中,首先采用反应谱法进行估算,用时程分析法作最后校核.但由于地震随机性的影响,时程分析法一般计算量非常大.本文采用人工生成的地震波,对金马大桥进行了地震响应研究,分析比较了多点线性一致激励、多点非线性一致激励以及多点行波效应输入情况下主梁、主塔、边墩等控制截面的内力和位移响应时程结果,并对其影响规律进行了详细地讨论.由于时域分析采用精细逐步积分格式,使计算结果更加精确,研究结果可以为同类桥梁工程的设计和计算提供参考.

1 非一致地震动输入下运动方程的建立

当结构的各支点的运动不同时,结构体系的运动控制方程可如下导出:结构体系相对于不动参考系的总位移向量表示为

式中:u pg为结构支撑点处的基础位移运动;u ps为结构的拟静力位移反应;u vs为结构的动力位移反应;p b为基础作用于结构上的力.将式(1)代入式(2),可得到

对于通常的工程结构,阻尼对上式右端项的影响不大,一般可以略去.由拟静力位移可知,拟静力位移与支点位移应满足

则可进一步写为

式中:R为影响矩阵,对于仅有某一方向的平移输入的情形,R的各行元素之和为1,即

注意:当地面作均匀一致运动且不考虑转动分量时,拟静力位移中所有沿 x方向的位移都和地面位移x g相同,而其他位移均为零,{¨u pg}={E}¨x g,方程(7)进一步可表达为

当需要考虑行波效应时,可以利用同一个地面运动加速度记录曲线在地面不同节点处以一定的时间差输入,由此产生式(7)右端的¨upg,如果要考虑各地面节点之间的部分相干性,则产生加速度过程较为复杂,而这类实测资料很少见.

2 精细逐步积分方法

钟万勰提出了一种求解动力学方程的高精度时程积分方法——精细逐步积分法[8-9].该方法的积分步长完全不受结构自振特性的制约,只要在所选时间步长内外载是线性变化的则无论该步长为多大,该积分格式总产生达到计算机精度的结构响应.即使外载随时间变化有一定程度的非线性,该方法比传统方法往往有更高的精度和效率.因此,它是一种无条件稳定的显式积分格式.本文在计算行波效应时的动力时程响应分析时采用了这种精细积分法.

精细逐步积分格式

1)运动方程

式中:C*,K*,p*分别为经振型正交化的阻尼、刚度和外荷载向量.结合等式y=﹒y,则上式即可将降阶为下列一阶微分方程

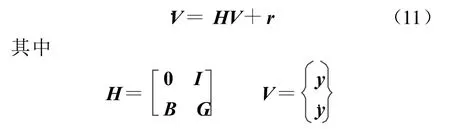
则方程(10)的齐次解为

式中

在积分步长 t∈[tk,tk+1]内,τ=t-tk.假定方程(10)的特解Vp(t)已经求出,则在本步长的初始时刻 t=tk,即 τ=0时 ,T(τ)=I(单位阵).由此可以确定积分常量C,得到方程的通解

问题归结为求解Vp(t)及精细地计算T(τ).

2)矩阵T(τ)的精细计算 在积分步长τ内部细分为m=2N等分

一般取n=20是足够的,于是 Δt=10-6τ.Δt一般远小于结构的所有自振周期.将式(17)代入式(15)中,得

3)线性荷载精细积分格式(HPD-L) 假定在每一积分步长t∈[tk,tk+1]内荷载变化是线性的,即

式中:r0和r1是时不变向量,则方程(26)的特解为

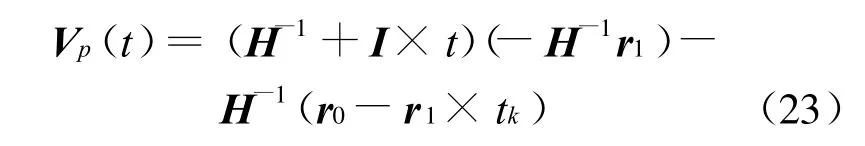
将式(23)代入方程的通解表达式,即得精细积分的HPD-L格式

3 金马大桥三维地震时程反应研究

协作体系金马大桥位于珠江三角洲西部,是广(州)肇(庆)高速公路上跨越西江的一座特大桥梁.桥梁全长1 912.6 m,其中主桥为双索面混凝土独塔斜拉桥与T型刚构的协作体系.斜拉桥双向对称悬臂长223 m,两侧T构双向对称悬臂长60 m,形成60 m+283 m+283 m+60 m的跨径组合,该桥283 m的跨度是目前世界上独塔混凝土斜拉桥的最大跨径.结构计算采用空间计算模型.本文斜拉桥主桥为边主梁结构,模型采用双主梁模型,中间桥面板采用厚板与之相连,横隔梁采用梁单元,连接方式是节点共用,计算模型共有3 009个节点,3 722个单元,其中梁单元为2 030个,板单元1 448个,实体单元132个,桁架单元112个,有限元计算模型图[10]略.

根据金马大桥桥位处地震烈度区划图可知,桥位处在峰值加速度为0.1 g的地区,按《公路工程抗震设计规范》,由反应谱人工合成地震波,本文以人工合成的地震波作为地震动输入,计算时采用了4组,每组10条,地震反应结果取其统计平均值.

3.1 线性和非线性时程响应分析研究

时程计算采用了2种情况:线性结构一致输入,非线性结构一致输入.阻尼比取0.05.动力时程分析中非线性结构一致输入主要考虑结构的几何非线性的因素的影响.因为金马大桥这种协作体系是一种柔性结构,在正常荷载作用下,其荷载和变形之间呈现出非线性,而且,这种非线性影响随桥跨的增大而愈益显著.在计算中考虑了主缆的垂度、主梁的弯矩和轴向力的耦合作用(即压弯耦合)以及地基土壤的非线性因素.并将线性和非线性的2种计算结果分别就下面结构的几个控制截面(见图1)取时程响应,并作了对比分析.

图1 金马大桥各个控制截面位置(单位:m)

3.1.1 纵向振动分量作用 金马大桥协作体系在纵向输入下结构的反应是较为显著的,主要表现纵向和竖向振动.对应于线弹性结构和非线性结构两种情况的响应,协作体系斜拉桥与T构连接处的最大纵向位移分别为:6.14 cm;6.10 cm,而塔顶处的最大纵向位移分别为5.17 cm;5.01 cm;可以看出,考虑非线性使协作连接处4截面和塔顶位移有少量的减小;改变量非常小;协作体系斜拉桥与T构连接处和斜拉桥塔顶的横向和竖向位移远远小于纵向位移,因此未列出.在该桥的动力特性中,竖弯振型和扭转振型是主要振型,这就不难解释,主梁的竖向位移、纵向位移和桥塔的纵向位移反应显著的原因.所以,桥面系面内的反应是主要的.

从内力的时程分析结果来看,在纵向地震波的作用下,对应于考虑结构的线性和非线性两种情况,截面 2的最大弯矩分别为:5.343×103,2.220×103kN◦m,在线性和非线性2种情况下,地震波分别传播在22.1 s和29.4 s左右,弯矩就达到峰值.从结果可以看出,非线性则使弯矩减小50%以上.

桥梁的下部结构通常是震害产生的部位,尤其是桥墩的震害,更要加以重视,因为桥梁在地震时的毁坏通常都是由下部结构开始的,比如,桥墩的破坏就有可能导致落梁的危险.在时程分析中取控制截面3,5和6,即主塔桥墩根部和T构薄壁墩以及边墩根部作为分析对象.考虑非线性会使截面3,5和6的弯矩或轴力、剪力减小.从截面3的轴力时程曲线可以看出轴力随时间有正负变化的规律,也就是说,在地震动的这段时间内,桥塔有时受拉,有时受压.边墩情况类似.篇幅所限仅给出截面2弯矩时程响应图2.

图2 纵向输入下截面2的弯矩时程

3.1.2 横向振动分量作用 协作体系桥在横向输入下结构的反应为斜拉桥主梁以及 T构和主塔横向振动.纵向和竖向振动反应很小.在横向地震波的作用下,对应于线性一致激励和非线性一致激励两种工况,截面2的最大弯矩分别为:2.876×103,1.788×103kN◦m,在线性和非线性两种情况下,地震波分别传播在28.1 s和31 s左右,弯矩就达到峰值.从结果可以看出,非线性则使主梁塔根弯矩减小35%以上.而且使得到达峰值的时间推延.

从位移的时程反应结果分析得出,在协作连接处4和塔顶1处非线性效应尤为明显.对应于线性、非线性结构2种情况下,在协作连接处4的最大横向位移分别为8.195,7.692 cm;峰值到达时间分别为31,33 s,考虑非线性会使跨中横向位移有微量的减小,而且使峰值出现时间推延,对应于以上2种情况的塔顶1处的横向位移分别为24.64,24.02 cm,可以看出,非线性仍使主塔位移微量减小,到达时间也有少量推延.协作体系斜拉桥与T构连接处4截面和斜拉桥塔顶1截面的纵向和竖向位移远远小于横向位移,因此未列出.篇幅所限仅给出斜拉桥与T构协作处截面4的横向位移时程图3.

图3 横向输入下斜拉桥与T构协作处截面4的横向位移时程

3.1.3 竖向振动分量作用 协作体系桥在竖向地震波的作用下主要表现为竖向和纵向振动,横向振动反应不明显.对应于线性结构和考虑几何非线性结构2种情况的响应,协作体系斜拉桥与T构连接处4的最大竖向位移分别为:3.41,2.98 cm,达到峰值的时间分别为21.3,22.6 s;而塔顶处1的最大竖向位移分别为0.243,0.135 cm;到达峰值时间分别为20.71,20.58 s;可以看出,考虑非线性仍使协作连接处截面4和塔顶截面1处位移有少量的改变;并且使得峰值到达时间也有少量的推延;协作体系斜拉桥与T构连接处和斜拉桥塔顶的横向和纵向位移远远小于竖向位移,因此未列出.

从内力的时程分析结果来看,在竖向地震波的作用下,对应于考虑结构的线性和非线性两种情况,截面 2的最大弯矩分别为:8.695×103,5.055×103k N◦m,在线性和非线性两种情况下,地震波分别传播在18.1 s和 20.6 s左右,弯矩就达到峰值.从结果可以看出,非线性则使弯矩减小35%以上,峰值到达时间推延.

在时程分析中取控制截面3,5和6,即主塔墩根部和T构薄壁墩以及边墩根部作为分析对象.发现考虑非线性会使截面3,5和6的弯矩或者剪力减小.篇幅所限仅给出截面5的纵向剪力时程响应图4.

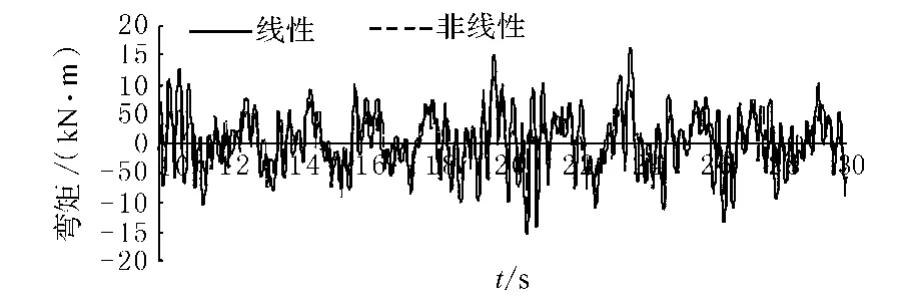
图4 竖向输入下截面5的弯矩时程

3.2 均匀地面运动和考虑行波效应地面运动的时程研究分析

行波效应主要指地震波在两个桥墩之间传播时并非同时到达,由于金马大桥的两个桥墩间距长达283 m,地震波在经过两个桥墩时会产生时间的滞后,即相位差.本文分别就均匀地面运动和考虑行波效应对协作体系金马大桥进行了P波,SH波,SV波作用下的时程研究分析,在时程积分过程计算中采用上面所述的精细逐步积分法,计算中阻尼比取0.02给出斜拉主桥主梁的内力峰值响应如图5,图.6,图7所示.

图5 P波下主梁轴力峰值响应分布(阻尼比0.02)

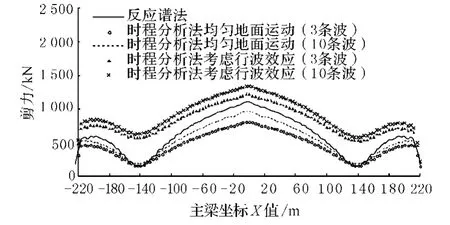
图6 SH波下主梁横向剪力峰值响应分布(阻尼比0.02)

从结果的比较可以看出,考虑行波效应之于这样的大跨径协作体系的影响是不可忽略的,其最大影响约为45%,同时表明忽略行波效应时的计算结构响应偏于不安全.

4 结 论

采用人工生成的地震波,分别就考虑结构的非线性和不考虑结构的非线性,考虑行波效应和不考虑行波效应的影响,对金马大桥在竖向、纵向和横向地震波输入下的地震反应进行了研究,分析比较了线性多点一致激励、非线性多点一致激励以及多点行波效应输入情况下主梁、主塔、边墩等控制截面的内力和位移响应时程结果,并对其影响规律进行了讨论.从三向正交分量作用下的计算结果来看:

1)几何非线性金马大桥的地震内力反应普遍降低20%～50%,但是对位移的影响却并不明显,大约在10%以内,因此采用线性理论分析可以得到更安全的结果.

2)从计算结果还可以看出:考虑行波效应会对对混凝土斜拉桥与T构协作体系产生有利或不利的影响,其不利情况可以达到线性一致输入情况下的1.2～1.7倍,在抗震设计时必须考虑.

3)对于金马大桥这样的特大跨度的协作体系除了考虑行波效应以外,还应考虑地震动的其它空间效应影响.目前很少看见有文献能够完全考虑这些空间效应,如相干效应和局部场地效应等,并且需要输入大量的地震波,取计算结果的统计平均值方能得到比较精确的结果,因此需要采用更新、更加精确的方法来计算

[1]张 哲.金马大桥设计实践与理论探索[J].大连理工大学学报,1999,39(2):285-293.

[2]李国豪.桥梁结构稳定与振动[M].北京:中国铁道出版社,1992.

[3]胡聿贤.地震工程学[M].北京:地震出版社,1981.

[4]范立础.桥梁抗震[M].上海:同济大学出版社,1997.

[5]范立础,胡世德,叶爱君.大跨度桥梁抗震设计[M].北京:人民交通出版社,2001.

[6]钟万勰,林家浩.大跨度桥梁分析方法的一些进展[J].大连理工大学学报,2000,40(2):127-135.

[7]林家浩,张亚辉,赵 岩.大跨度结构抗震分析方法及近期进展[J].力学进展,2001,31(3):350-360.

[8]钟万勰.结构动力学的精细时程积分法[J].大连理工大学学报,1994,34(2):131-136.

[9]林家浩,钟万勰.结构非平稳随机响应方差矩阵的直接精细积分计算[J].振动工程学报,1999,12(1):1-8.

[10]余报楚.混凝土斜拉桥与T构协作体系的极限承载力及动力响应研究[D].大连:大连理工大学土木工程学院,2006.