班轮联盟集装箱舱位互换规划与决策模型

陈继红 真 虹)

(上海海事大学交通运输学院1) 上海 200135) (上海国际航运研究中心2) 上海 200082)

Strategic alliances is very important in liner shipping industry.Shipping companies can cooperate by the exchange of container slot[1].

Cho and Perakis[2]established linear models or fleet and route optimization;Teodor Gabriel Crainic[3]studied the designing of cargo network.Brian Slackc,Claude Com tois,Robert M ccalla[4]studied strategic alliance of shippingw ith global view s.Chen Jihong,Zhen Hong,Zong Beihua[5]estab lished a new linear model for slot chartering.With themerger and alliance,scholars paid more attention to shipping alliance.

1 Conventional linearm odel

The conventional linear m odel for liner shipping,w ithout cooperation,isas follow s[6-7]:mins.t.

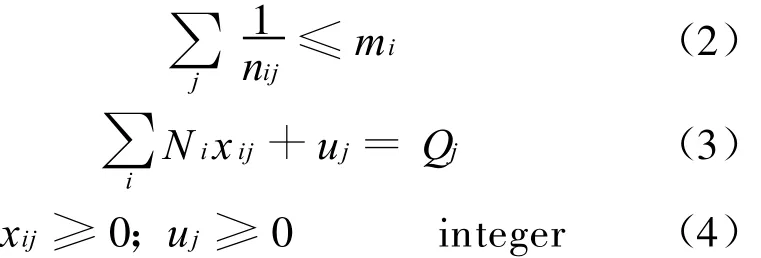
Param eters exp lanation for the above model are as follow s:i is symbol for ships;j is sym bol for routes;cij is transport cost of a consecutive voyages for ship i in route j;Z0is costs of shipping system;δj isopportunity cost for each TEU(twenty equivalentunit)in rout j;mi is number o f ship i;nijismaxim um consecutive voyages for ship i in route j;N i is capacity(TEU)of ship i;Qj is forward shipment(TEU)in route j;xij is decision variab le,number of consecutive voyages for ship i in route j;uj is decision variable,uncarried TEU in rout j.

Branch-bound method and cutting-plane al-gorithm[8]are theoretically effective.MATLAB program is useful and effective[9].Exp lanation o f the param eters and formu las for the above m odel is almost the same as the follow ing model.

2 Nonlinear integer model for slot exchange

This model is a non linear integer model[10].Decision variables are as follow s,,,,,,etc.Specially,andshould be confined with the conventional linear m odel.

2.1 Parameters exp lanation

S:set for shipping alliancesm em bers,∀l∈S;∀h∈S;l≠h;l,h:symbol for com pany,l≠h;k,i:symbol for ships,k for com pany h,i for company l;j:symbol for liner shipping routes;:costs of system of company l,h.:transport cost of a consecutive voyage of company l,h for ship i,k in route j;,:opportunity cost of com pany i,h for each TEU in rout j;,:slot costof one TEU of ship i,k in route j offered by com pany l,h:number of ship i,k from company l,h;,:maximum consecutive voyages for ship i,k of company l,h in route j;,:capacity o f ship i,k of company l,h;,:forward shipment of company l,h in route j,:decision variab le,number of consecutive voyages for ship i,k of com pany l,h in route j;,:decision variable,num ber of cooperative consecutive voyages for ship i,k of company l,h in route j;,:decision variable,num ber of slots for exchange,offered by com pany l,h,from ship i,k in route j for each consecutive voyages.,:decision variable,un-carried TEU of company l,h in rout j.

2.2 Formulas exp lanation

Form ula(5)means system cost shou ld be m inimized;formula(6)and(7)mean system cost should be notmore than that without cooperation;formu la(8)and(9)show number of cooperative voyagesmay be less than a fixed number;formula(10)and(11)mean the largest number of the ships;formula(12)and(13)show the carrying tasks;formula(14)and(15)m ean that cooperative voyage and container slots forexchangew illexistat the same time;formula(16)to(21)are non-negativity or integral or other restrictions.

2.3 Algorithm for the nonlinear integerm odel

There is no much effective algorithm for non linear integer model[10].This paper app lied an ant colony optimization algorithm[11-12].Ant algorithm s aremu lti-agent system s,called artificial ant.

Choose n variables as n-level decision-making problem.There are Finodes for i-level.Initially,artificial ants are at the first level.Each ant builds,starting from the source node,a solution by app lying a step by step decision policy.W hen located at a level j,the ants use the pherom one trailτijto compute the p robability of choosing node i:

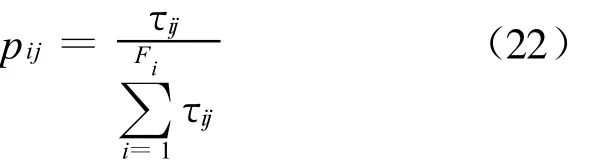
W hen the arc(i,j)is traversed,the pheromone value changes:

whereρis the evaporation rate and lies in between[0,1].Usually,we can setρ∈[0.5,0.9].The parameter Q represents a positive number;and f is the objective function value.By using this rule,the probability increases that forthcoming antsw ill use this arc.Major procedure for the algorithm is as follow s:(1)set parameters and initialize pheromone(set circle number cn,τij,Q,p);(2)Put m ants at the first level;(3)each ant get n nodes,using the pheromone trailτij to compute the probability of choosing node i;(4)compute the ob jective function value f,if f ＜ the given num ber,←+,and cn←cn+1;(5)if cn＞the given number,stop;otherw ise go to(2).The model invo lvesmany variab les,w e can deal w ith it w ith the help of MATLAB.

3 Application&data simulation

We suppose two shipping companies A and B cooperate in form of slot exchange.A and B cooperate foreach voyage in 4 container shipping route;and the largest number of slot exchange for the two companies is half of each ship＇s capacity.Planning period is a quarter of a year.Specific data can be got from Table 1～3.

Table1 Freight volume(TEU)for each company

Table2 Largest number o f voyages for each ship in the rout

Table 3 Different kinds of costs for one consecutive voyage or one TEU(thousand USD)

Firstly,w e can use the conventional linear m odel for p lanning of com pany A and B respectively.The results form MATLAB in Table 4.

From Table 4,we know w ithout slot exchange,shipping system total cost are as follow s=97 700 for A;and=34 050 for B.A nd summ ation of the total cost is 131 750.

Table 4 Number of consecutive voyages for each company and the total cost(thousand USD)

3.1 Decision-making for slot exchange

W ith the help of MATLAB,results of the nonlinear integermodel for slotexchange are listed from Table 5 to Tab le 7.

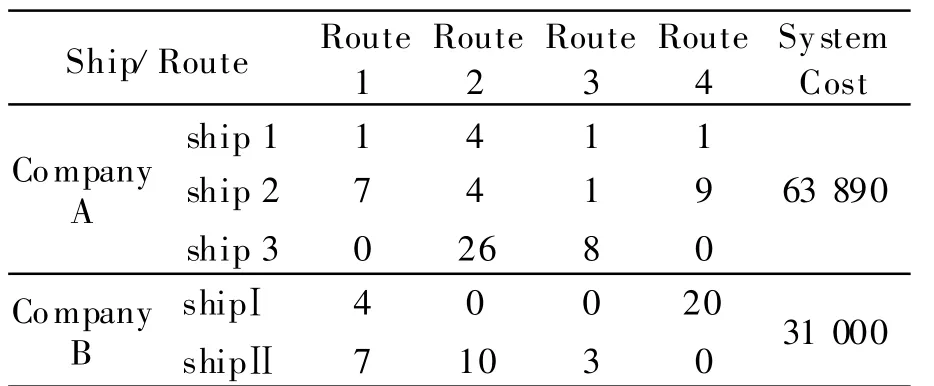
Table 5 Number of consecutive voyages for each com pany under shipping alliance and the total cost(thousand USD)

Table6 Number of cooperative voyages offered under shipping alliance

Table7 Number of container slots(TEU)offered by each company for each consecutive voyage

Com paring Tab le 5 w ith Table 4,the total cost for A and B all descend by a large scale.For A,system cost descend to 63 890,descending by 34.6%;and for B,system cost descend to 31 000,descending by about 9.0%.And the total cost descends to 94 890,descending by about 28%.

3.2 Sensitivity analysis

Let the freight task of each route vary by a small scale continuously,the change of system cost for two companies will be observed.The fluctuation range can be referred to following figures.From the figures,we know route 1 and route 3m ay bem ore beneficial to cooperation of the companies.In the figures:

COSTA,COSTB:system cost of company A,B;RATE:percentage(%)of the change of freight task of the route;M EAN:value o f system cost.

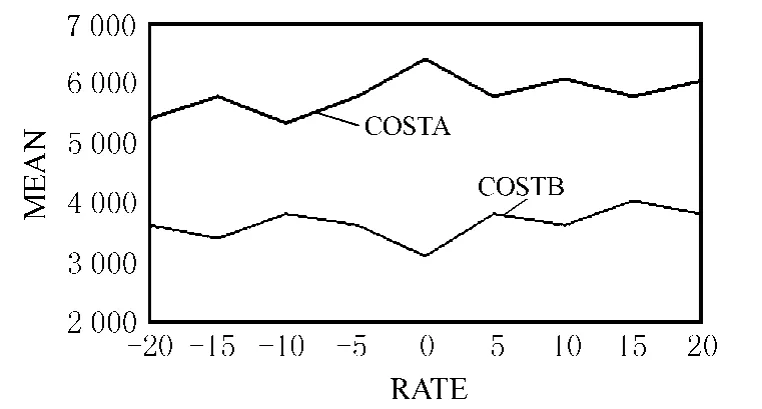
Fig.1 Sensitivity analysis for Route 1

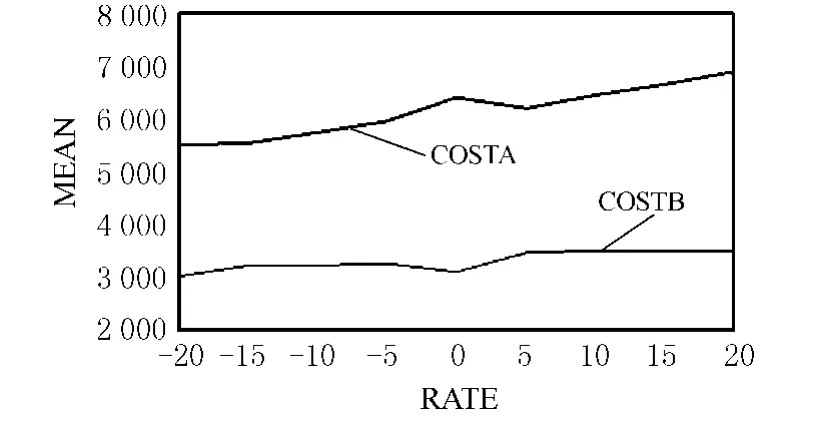
Fig.2 Sensitivity analysis for Route 2

Fig.3 Sensitivity analysis for Route 3

Fig.4 Sensitivity analysis for Route 4

4 Conclusion

Slot exchange is thebasic and effective form o f cooperation for shipping alliance.This study offered a nonlinear integer model as a decisionsupport too l to reduce system cost and management performance of liner shipping alliance m em bers.The proposed new model can help p lanners maker better decision m aking under shipping-alliance constrains.Additionally,the m odelw as exp lained using a case study.Experimental results show the proposedmodelhasbetter app licability and performance than conventionalmodels.

[1]Ding Yusong.Basic form and main elements of the agreement for cooperation for container liner routes[J].Containerization,2003,14(1):15-17.

[2]S.C.Cho,A.N.Perakis.Optimal liner fleet routing strategies[J].Maritime Policy and M anagement,1996,23(3):249-259.

[3] Teodor Gabriel Crainic.Service netw ork design in freight transportation[J].European Journalo f Operational Research,2000,122(2):272-288.

[4]Slack B,Claude Com tois,Robert M cca lla.Strategic alliance in the container shipping industry:a global perspective[J].Maritime Policy &Management,2002,29(1):65-76.

[5]Chen Jihong,Zhen Hong,Zong Beihua.Imp roved vessel allocationmodel o f liner shipping and its app lication for slot chartering under shipping alliance[J].Journal of Transportation Systems Engineering and Information Technology,2008,8(3):120-125.

[6]Zhao Gang.Analysis and im provement on the vessel allocation model of liner service[J].Journal of Systems Engineerings,1997,12(1):80-86.

[7] Xie Xinlian.M ethods for ship scheduling and fleet planning[M].Beijing:Peop le＇s Traffic Press,2000.

[8]N iu Yingw u.Operation Reasearch[M].Xi＇an:Xi＇an Jiao Tong University Press,2005.

[9]Wang Jinghui,Qiao Weim ing.A general algorithm of solving linear integer p rogramm ing and its MATLAB app lication[J].Computer Engineering,2005,31(6):20-24.

[10]Lu ChinShan,Lai Keehung,Cheng T C E.App lication of structural equation modeling to evaluate the intention of shippers to use Internet services in liner shipping[J].European Journal of Operational Research,2007,180(2):845-867.

[11] Li Shiyong.Ant colony algorithm and application[M].Harbin:H arbin Institute of Technology Press,2004.

[12]Gao Shang,Yang Jingyu.Ant colony op tim ization algorithm for non linear integer p rogramm ing[J].Journal of Nanjing University of Science and Technology,2005,29(10):120-123.