基于贝叶斯网络的控制回路关联故障诊断

赵顺毅 刘 飞

(江南大学自动化研究所，无锡 214122)

现代工业中任何一个控制系统都要求高的控制性能.一个好的控制系统能够增加产量，减少消耗，提高整个企业的效益.因此控制性能的评估以及监视器的应用在过程工业中已经逐渐成为主流，并且正在逐步地改变主流的控制方法，从先前的基于预测的控制逐步转变到基于条件的控制［1］.对于控制性能的评估在过去几十年里得到了快速的发展，已经提出了空间辨识、高阶统计分析、非参数模型的神经网络等方法［2］，同时发展的还有控制回路的故障诊断.但是大部分研究均是针对控制回路出现的特殊问题提出解决方法，如执行结构的问题和模型失配问题，很少有研究提出一种系统化的方法来进行控制回路的诊断.对于在回路出现的故障之间可能存在交叉相关的情况下建立一个控制回路诊断系统的研究就更少.构建一个对整个控制回路进行监控诊断的系统有诸多困难.首先，尽管故障可能不同，但是由故障所带来的现象可能相同.二是所有回路都是在不确定的环境下进行操作的，所表现出来的现象都是通过一定的概率联系其原因的，因此必须在概率的框架下来给出解决问题的方案.另外，由于现在大部分的监控器都是基于数据的，因此在诊断系统中引入先验的知识来改善诊断性能是非常有必要的［2］.建立一个包括控制回路中所有的监控器在内的一个控制回路诊断监控系统，用其来监控回路的控制性能以及调整回路中设备的故障是可行且是必要的.现有的大部分针对控制回路诊断的方法大致可以分为基于模型和基于过程历史数据［3－5］.一个控制系统中有多个控制回路，在实际应用中受到机械、电物理、化学等因素影响，表现出来的故障之间也会产生交叉影响，使得故障之间存在许多不确定的因素，如果在诊断的过程中不考虑这些因素，势必会影响诊断结果的准确性.

近十几年发展起来的贝叶斯网络技术，适合用于表达和分析不确定性的事物，而且还具备了描述事物多态性和非确定性逻辑关系的能力，在经济预测、医药等领域都得到了广泛的应用.随着其不断的发展，贝叶斯网络的学习和表达能力得到了很大的提高.本文应用贝叶斯网络良好的结构学习能力来构建一个控制回路的诊断系统，利用贝叶斯网络良好的推理能力进行控制回路的故障诊断，并通过一个具体的实际应用，证明贝叶斯网络模型在控制回路处于不确定环境下构建控制回路的诊断系统的有效性.

1 模型的建立

1.1 控制回路的基本模型

一个典型的控制回路通常由控制器、执行机构、控制对象、传感器等构成，如图1所示.

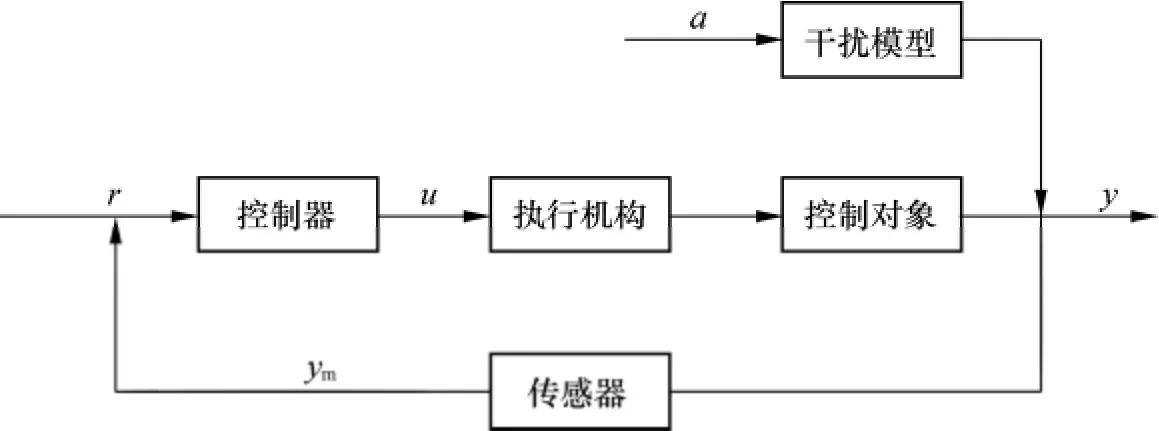
图1 控制回路的基本结构

这4个组成部分均可能出现一些不同的问题，例如执行机构的非线性问题、传感器输出偏差问题.这些问题均会造成控制性能的降低，以致影响到其产品的产出率以及质量.因此本文的目标就是通过利用贝叶斯网络的特性，在回路的控制性能没有达到要求的情况下找出造成性能低下的原因.

本文假设控制对象的模型是已知的，并且对控制回路的各个组成部分均有各自的监控器对其进行监控.每个监控器对不是其主要监控的对象也会有敏感的反应，例如传感器监控器主要监控传感器的偏差问题，但是它对执行结构的非线性也会产生相应的信号.一个完整的控制回路诊断系统包括了执行机构监控器、模型监控器、传感器监控器和控制性能监控器.由于过程模型包括对象模型和干扰模型，因此需要2个模型监控器来区别是对象模型变化还是干扰模型变化.控制性能监控器的评定指标可以是最小方差也可以是其他一些用户自定义的指标.由于系统是在不确定的环境下工作的，出现的问题之间彼此会产生联系，一般的控制回路诊断结构如图2所示.其中实线表示故障之间确定的关系，虚线表示故障在不确定的环境下彼此之间可能会存在的相互关联.

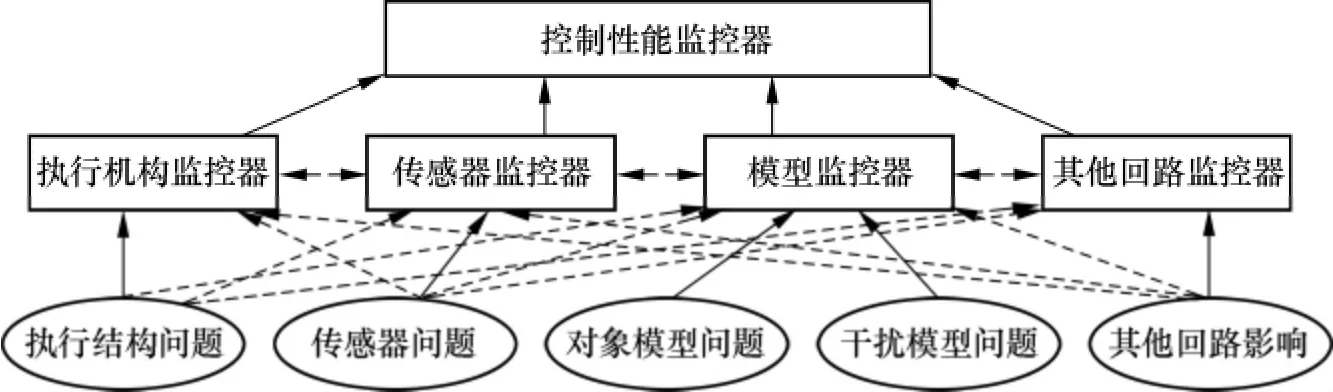
图2 控制回路诊断问题

1.2 贝叶斯网络及其结构算法

贝叶斯网络又叫有向非循环图(DAG)，是一种基于概率的网络，其用有向的图来表示变量之间的因果关系.网络中的每个节点表示一个随机变量，有向线段表示变量之间的条件概率关系.因此整个贝叶斯网络可以表示为N={P，∂}，其中P是有向非循环图，∂为条件概率，可以根据如下贝叶斯公式求解:

假如A变量具有n个状态值，且每个状态均为一个有限的值，则有

贝叶斯网络的建造是一个复杂的任务，需要知识工程师和领域专家的参与［6］.在实际中可能是反复交叉进行不断完善的.现在关于建立贝叶斯网络的方法也有很多，如故障树法等［7］.一般来说构建贝叶斯网络可分为以下步骤:

①首先根据实际问题确立贝叶斯网络各个节点的意义，确定各个节点之间的关系，并且各个节点数据要尽可能地包括可能出现问题的所有状态.

②利用有向图表示各个节点之间的关系，用子节点和父节点的连线确定贝叶斯网络的结构，并且由各个节点的概率计算各个节点之间相互之间的条件概率.

③每个节点的父节点必须给定一个先验概率.

一个完整的贝叶斯网络结构，即能充分包含不确定性信息的结构，是贝叶斯网络进行不确定性推理的前提和基础.网络的拓扑结构通常是根据具体的研究对象来确定的.由于控制回路的故障存在不确定问题，故障之间很可能会有交叉关联，根据专家知识建立起来的网络不能高准确率地表示故障节点，因此利用获得的数据对网络结构进行学习，可使建立起来的模型更加准确［8］.本文应用K2算法.K2算法采用贪婪搜索处理模型选择问题:先定义一种评价网络结构优劣的评分函数，其评分函数定义为网络结构的最大后验概率.再从一个节点开始，根据事先确定的最大父节点数目和节点次序，选择分值最高的节点作为该节点的父节点.在搜索过程中K2按顺序逐个考察变量顺序中的变量，确定其父节点，然后添加相应的边.例如在对某一变量Xi进行搜索时，假设已经找到其父节点，如果父节点的数目还未达到上限，那么继续寻找父节点.具体做法就是先考虑在变量顺序中排在Xi前的但还不是Xi的父节点的变量，从中选出Xj，使得新家族评分达到最大，然后与旧家族评分比较，如果比旧家族的评分高，则添加Xj为Xi的父节点，否则停止寻找.该算法在数据完备的情况下能很好地学习到拟合数据的网络结构.

1.3 控制回路诊断系统的贝叶斯网

建立一个基于贝叶斯网络的控制回路诊断系统的流程，如图3所示.本文所研究的是在完备数据集的基础上建立控制回路诊断系统，不考虑数据的丢失问题，所以实例收集的数据就是试验中所用的完备数据集.

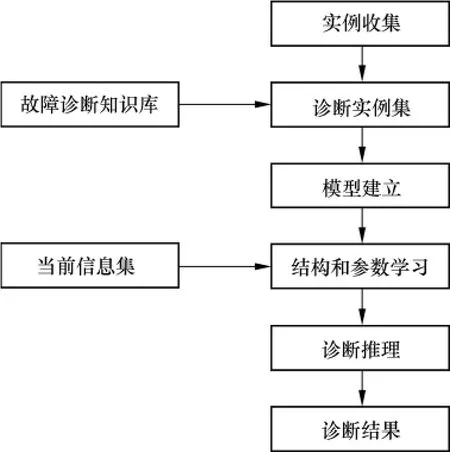
图3 贝叶斯网络流程构建

2 在控制回路诊断系统中的应用

现代工业应用中的控制系统均是多回路系统，各个回路均处在不确定的环境中.为了研究基于贝叶斯网络的控制回路诊断系统的有效性，本文将贝叶斯网络应用到一个工业蒸馏塔中［9］.

2.1 蒸馏塔故障模型

蒸馏塔是目前过程工业中常见的多输入多输出控制系统，由多个控制回路组成，各个回路之间均会有相互联系.假设蒸馏塔的多个控制变量中3个变量是本文所感兴趣的:蒸馏塔顶上的温度、底部的温度和塔中的气压.蒸馏塔控制中出现的主要故障可以通过专家知识获得，以收集相关用于该故障诊断的信息.造成蒸馏塔控制性能指标低下的原因主要有底部温度模型的失配和传感器的偏差等.具体的故障如表1所示.

表1 蒸馏塔故障表

对于上述故障，每一个网络节点均表示一个故障状态或者故障原因.让网络对采集的完备样本集进行结构学习和参数学习，在此参数学习采用最大后验概率法.在Matlab中嵌入FullBNT工具箱后编写M程序后运行.

2.2 仿真结果及评价

在Matlab环境下通过K2算法学习到的网络结构如图4所示.图中M为控制回路性能监控器，每个节点都有2种状态，正常与不正常，均用概率值表示.图4所表示的网络结构中，节点A3和B3，D1和B3，D1和C3之间均具有有向线段，表明故障之间存在着相互关联，即执行结构的问题会对传感器监控器产生影响，其他回路对该控制回路的控制性能也有相应的影响.这种通过数据学习所得到的贝叶斯网络，能够很好地弥补专家知识建模带来的局限性，使得模型结构最大程度地拟合实际数据，从而提高了故障诊断的精确度.试验中通过检测到的完备样本数据输入到构建好的贝叶斯网络中去.通过推理得到的该蒸馏塔不同故障发生的概率表，如表2所示.

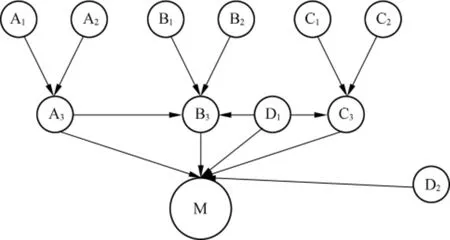
图4 蒸馏塔贝叶斯网络结构

表2 故障概率表

可以看到，在该控制回路中有很多种可能出现的故障会导致控制回路的控制性能低下.通过贝叶斯网络的推理，可以发现故障A1，A2，A3发生的可能性均比较大，因此当回路的控制性能未达到相应指标时，可以先检查燃气供应阀门和圆顶阀门是否存在粘滞问题，以及执行结构监控器是否受干扰的影响导致其误输出.这与实际情况十分吻合，这样可以避免大量繁琐无用的检修，快速准确地找到故障所在.该网络模型对其故障诊断输出的是一个概率值，但这并不影响实际的应用，因为只要得到概率的大小是按实际故障出现的几率大小所分布的即可，在应用中这与得到一个准确的数值的效果是一样的.

如果采用一般的专家系统对该控制回路进行建模，无法对该控制回路中可能出现的故障之间的关系做出一个很好的表达，即会忽略故障彼此之间的关联性，从而使得故障诊断结果产生比较大的误差，给故障排除带来一定的困难，造成大量不必要的检修.

3 结语

本文利用贝叶斯网络很好的结构学习能力和不确定性表达能力构建了一个控制回路诊断系统，该系统整合了所有控制回路中对于不同问题进行监控的监控器，很好地避免了回路中出现的故障可能交叉相关这一情况给诊断结果造成的影响.仿真表明该诊断系统能够很好地监控控制回路的控制性能，当控制性能低下时，能够快速准确地找出造成其性能低下的原因，具有较高的诊断精度.

References)

［1］Thornhill N F，Shah SL，New directions in control loop assessment and diagnosis［J］.Computing and Control Engineering，2005，16(4):18-22.

［2］Huang Biao.Bayesian methods for control loop monitoring and diagnosis［J］.Journal of Process Control，2008，18:829-838.

［3］Venkatasubramanian V，Rengaswamy R，Yin K，et al.A review of process fault detection and diagnose.partⅠ:quantitative model based methods［J］.Computers and Chemical Engineering，2003，27(3):293-311.

［4］Venkatasubramanian V，Rengaswamy R，Yin K，et al.A review of process fault detection and diagnose.partⅡ:qualitative models and search strategies［J］.Computers and Chemical Engineering，2003，27(3):313-326.

［5］Venkatasubramanian V，Rengaswamy R，Yin K，et al.A review of process fault detection and diagnose.partⅢ:process history based methods［J］.Computers and Chemical Engineering，2003，27(3):327-346.

［6］李俭川，陶俊勇，胡茑庆，等.基于贝叶斯网络的智能故障诊断方法［J］.中国惯性技术学报，2002，10(4):24-28.

Li Jianchuan，Tao Junyong，Hu Niaoqing，et al.Intelligent fault diagnosis technique based on Bayesian networks［J］.Journal of Chinese Inertial Technology，2002，10(4):24-28.(in Chinese)

［7］周忠宝，马超群，周经伦.基于贝叶斯网络的事故序列分析［J］.哈尔滨工业大学学报，2009，41(9):191-193.Zhou

Zhongbao，Ma Chaoqun，Zhou Jinglun.Accident sequence analysis based on Bayesian networks［J］.Journal of Harbin Institute of Technology，2009，41(9):191-193.(in Chinese)

［8］刘明辉，王磊，党林阁，等.非确定先验信息的贝叶斯网络结构学习方法［J］.计算机工程，2010，36(5):165-167.Liu Minghui，Wang Lei，Dang Linge，et al.Structure learning method of Bayesian network with uncertain prior information［J］.Computer Engineering，2010，36(5):165-167.(in Chinese)

［9］Volk U，Kniese D W，Hahn R，et al.Optimized multivariable predictive control of an industrial distillation column considering hard and soft constrains［J］.Control Engineering Practice，2005，13(7):913-927.