L无穷范数软间隔支持向量机分类

罗林开 张晓东

(厦门大学自动化系，厦门 361005)

20世纪90年代，Vapnik［1］提出了一种新的数据挖掘方法——支持向量机(support vector machine，SVM).SVM在统计学习理论基础上，引入VC维［2］，采用最大间隔原理和结构风险最小化原则(SRM)［3-5］，实现了经验风险与置信风险的折中，较好地解决了非线性、高维数、局部极小点等问题，同时又具有很好的泛化能力.

对于线性可分的二分类问题，存在一个正确划分2类样本同时具有最大间隔的超平面.对于线性不可分问题，通过引入松弛变量ξ对间隔进行软化［6-8］，利用ξ度量经验风险;同时，在优化的目标函数中引入C对ξ进行惩罚，实现经验风险与置信风险的折中.常用的SVM模型有L1-SVC和L2-SVC两种［1，3-4］.L1-SVC的目标函数可表示为，其中经验风险是ξ的1范数;L2-SVC的目标函数可表示为，其中经验风险是ξ的2范数的平方.

目前，经验风险用ξ的无穷范数来度量的SVM模型尚未见文献报道.由于无穷范数比1-范数和2-范数具有更好的鲁棒性，因此用ξ的无穷范数来度量经验风险，可期待取得比常用的L1-SVC与L2-SVC模型更好的泛化性能.为此，本文提出了一种无穷范数软间隔支持向量分类机(L-infinity-SVC)模型，并通过实验分析其性能.

1 L-infinity模型及算法

在软间隔支持向量分类机中，当经验风险采用ξ的无穷范数度量表示时，无穷范数软间隔支持向量分类机模型可表示为

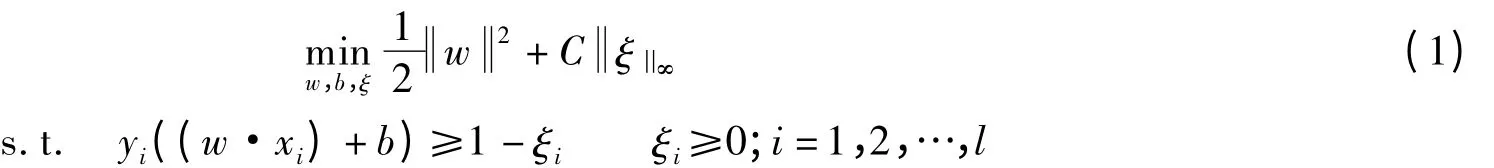
该模型等价于

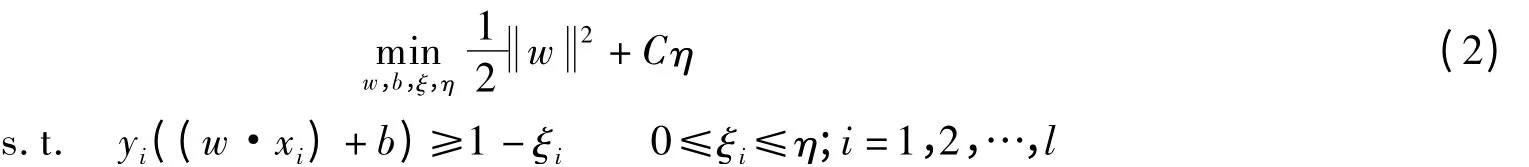
对于线性不可分程度很高的问题，模型(2)可能依然不理想.这时可通过一个非线性映射Φ将输入空间映射到一个高维的Hilbert空间H中［9-10］，然后在H中选择最优超平面划分成2类样本.此时模型(2)演变为

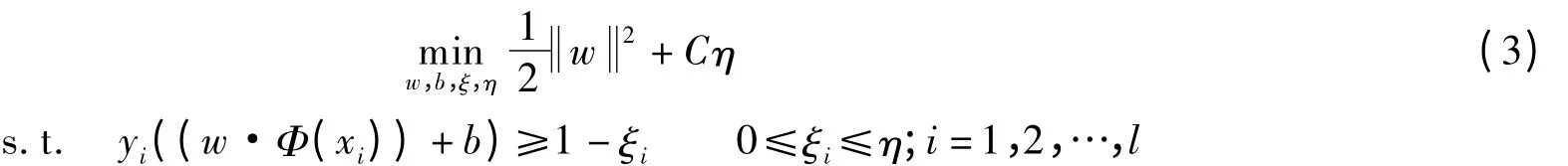
H中样本的内积为

可将此内积称为输入空间上样本间的核函数.可以证明，H中的最优分类超平面仅依赖于核函数，并不需要非线性映射Φ的完整定义.常用的核函数有线性核函数、多项式核函数、高斯径向基核函数和Sigmoid核函数等.

下面研究模型(3)的对偶问题、原问题及对偶问题最优解的关系.

定理1 原始最优化问题(3)的对偶问题为

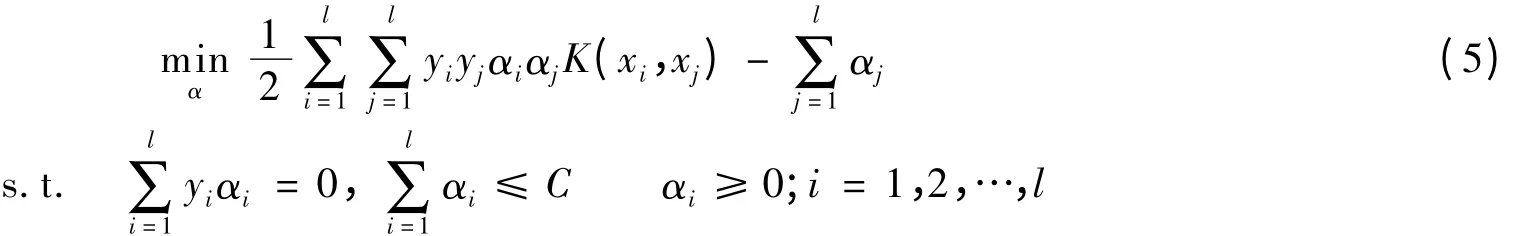
证明 原问题(3)相应的Lagrange函数为

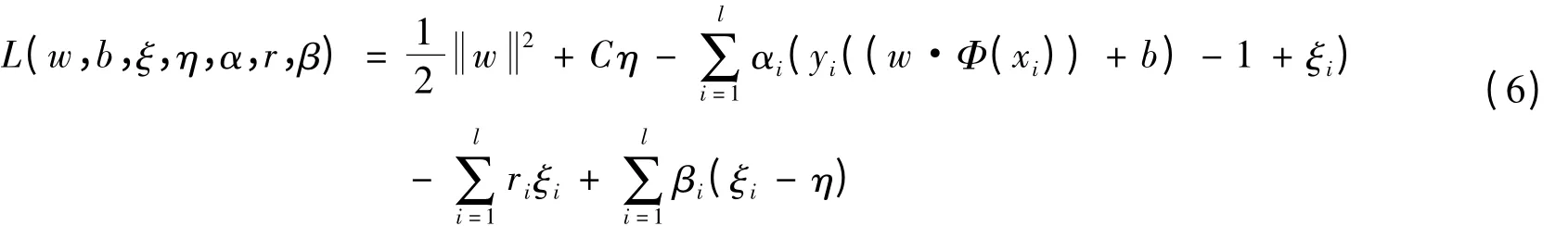
式中，αi≥0;ri≥0;βi≥0.根据Wolfe对偶定义［3］，L关于w，b，ξ，η求极小，即

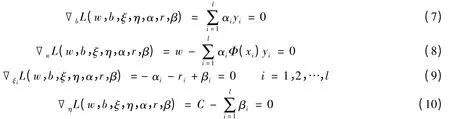
整理得

代入式(6)中，整理得对偶问题可表示为

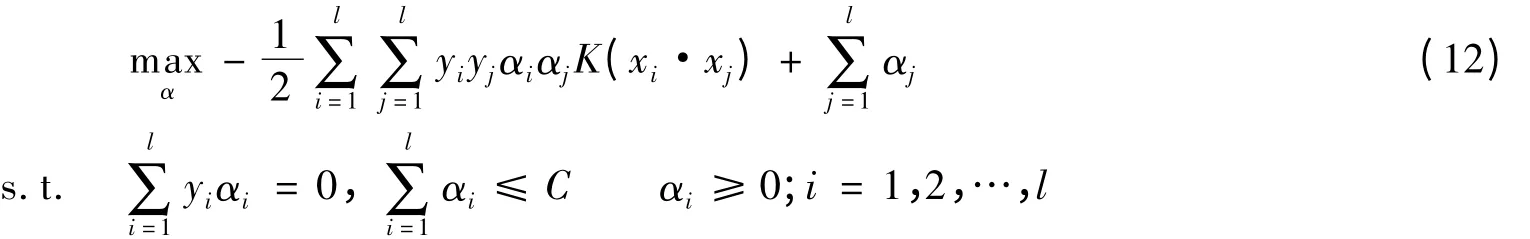
显然，式(12)与(5)等价.

定理2 设α*={α1*，α2*，…，α*l}T为对偶问题(5)的解，若存在α*的分量α*j，α*k＞0，yjyk＜0，则原问题(3)的解(w*，b*)可以表示为

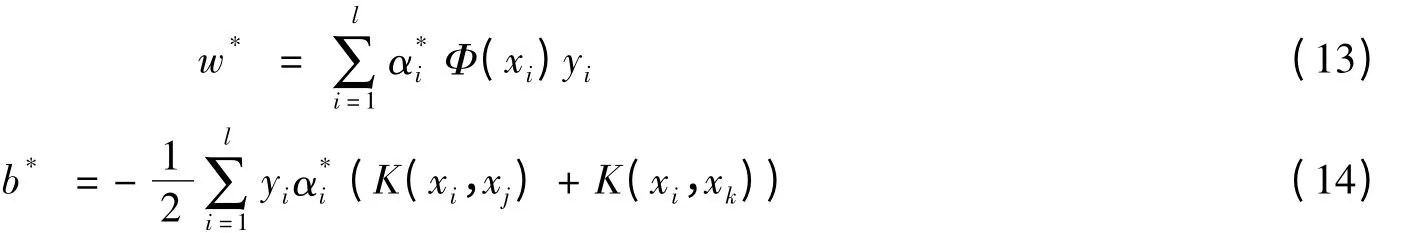
证明 根据对偶问题的推导可知

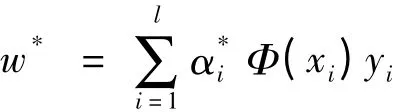
即式(13)成立.令H=(yiyjK(xi，xj))l×l，e={1，1，…，1}T，α={α1，α2，…，αl}T，y={y1，y2，…，yl}T，则对偶问题可以表述为

这个问题的Lagrange函数可表示为

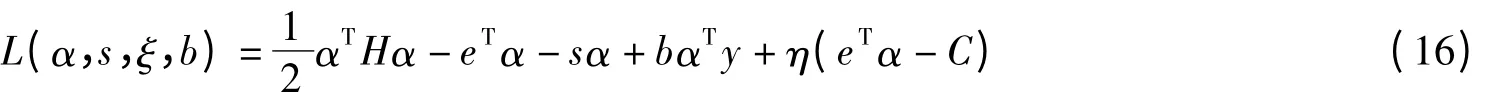
α*为式(5)的最优解的KKT条件为

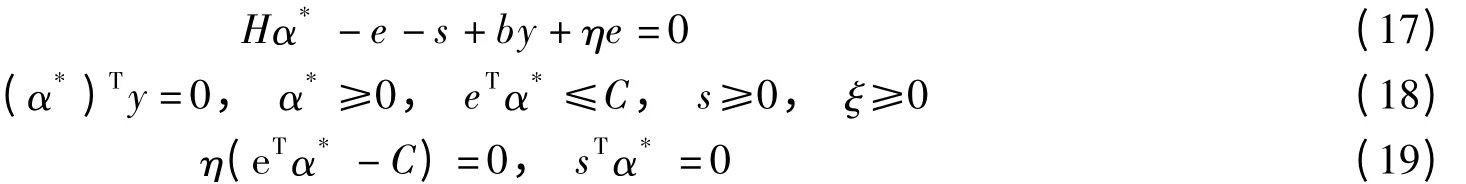
由式(13)可知，式(17)可等价为

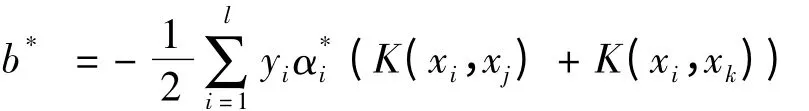
根据上述2个定理可建立了L1-SVC模型的另一种变形L-infinity-SVC，算法如下:

①设已知训练集T={(x1，y1)，(x2，y2)，…，(xl，yl)}∈(X×Y)l，其中xi∈X=Rn，yi∈Y={1，－1}，i=1，2，…，l.

②选择适当的核函数K(x，x')和适当的参数C，构造并求解最优化问题(5)式，得到最优解α*=

③选择α*的2个正分量，yjyk＜0，并计算阈值

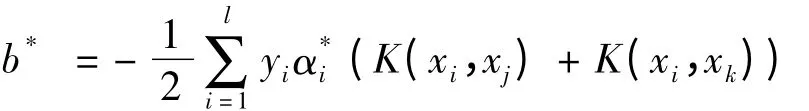
④构造决策函数

2 实验结果与分析

ξi度量了训练样本xi的经验风险，ξi的值越大表明xi被错分的程度越大，即经验风险越大.在L-infinity-SVC经验风险的控制中，对其最大的经验风险进行最小化;而在L1-SVC和L2-SVC中，最小化的是各个训练样本点上的平均经验风险.因此，在测试集的误判率方面，相比于L1-SVC和L2-SVC，L-infinity-SVC将会获得更接近于训练集上的误判率;也就是说，L-infinity-SVC在测试集上的准确率和训练集上准确率会比L1-SVC和L2-SVC更高，L-infinity-SVC具有比L1-SVC和L2-SVC更好的泛化性能.

为了检验L-infinity-SVC的泛化性能，在基准数据集上进行L1-SVC，L2-SVC与L-infinity-SVC的比较试验.试验中的数据集为Heart和Sonar，它们均来自UCI数据集［11］，都是二分类问题.核函数为线性核函数，运用Matlab的二次规划问题算法进行小规模问题求解.训练集与测试集样本的比例为1∶1，实验结果见表1.

表1 L1-SVC，L2-SVC与L-infinity-SVC的训练与测试准确率 %

从表1可以看出，在Heart数据集上，L-infinity-SVC测试集准确率与训练集准确率的相对误差为20.59%，小于L1-SVC的24.65%和L2-SVC的24.35%;在Sonar数据集上，L-infinity-SVC测试集准确率与训练集准确率的相对误差为24.40%，小于L1-SVC的25.35%和L2-SVC的25.40%.实验结果表明，L-infinity-SVC测试集上准确率与训练集上准确率接近程度优于L1-SVC和L2-SVC.

3 结语

本文提出了一种L无穷范数软间隔支持向量机模型，并导出了其对偶问题和分类超平面的计算公式.L-infinity-SVC具有比常用的L1-SVC和L2-SVC更好的泛化性能，其测试集准确率与训练集准确率的接近程度优于L1-SVC和L2-SVC.但L-infinity-SVC更容易受噪声点影响，因此，如何克服噪声点的影响以及大规模问题时L-infinity-SVC的有效求解是下一步要考虑的工作.

References)

［1］Vapnik V N.The nature of statistical learning theory［M］.New York:Springer，2000.

［2］Vapnik V N，Levin E，Cun Y L.Measuring the VC-dimension of a learning machine［J］.Neural Computation，1994，6(5):851-876.

［3］邓乃扬，田英杰.数据挖掘中的新方法——支持向量机［M］.北京:科学出版社，2004.

［4］Burges C J C.A tutorial on support vector machines for pattern recognition［J］.Data Mining and Knowledge Discovery，1998，2(2):121-167.

［5］Franc V，HlaváěV.An iterative algorithm learning the maximal margin classifier［J］.Pattern Recognition，2003，36(9):1985-1996.

［6］Cortes C，Vapnik V N.Soft margin classifier［EB/OL］.(1997-06-17)［2010-06-15］.http://www.freepatentsonline.com/5640492.html.

［7］Chen D R，Wu Q，Ying Y M，et al.Support vector machine soft margin classifiers:error analysis［J］.The Journal of Machine Learning Research，2004，11(5):1143-1175.

［8］Schawe-Taylor J，Cfistianini N.On the generalization of soft margin algorithms［J］.IEEE Trans on Information Theory，2002，8(10):2721-2735.

［9］Mangasarian O L.Mathematical programming in machine learning［M］.New York:Plenum Press，1996:283-295.

［10］Amari S，Wu S.Improving support vector machine classifiers by modifying kernel functions［J］.Neural Networks，1999，12(6):783-789.

［11］Blake C L，Merz C J.UCI repository of machine learning databases［EB/OL］.［2010-06-15］.http://www.ics.uci.edu/～mlearn?MLRepository.html.