简化的动态因子分析过程监控方法及其应用

尹雪岩 刘 飞

(江南大学自动化研究所，无锡 214122)

过去几年间，工业技术革新取得了长足的发展，企业对于产品质量以及生产安全的重视使得过程监控技术的改进日臻完善.同时企业信息化水平不断提高，大量生产、调度以及供应链的数据得以采集.因此，基于数据驱动的多元统计过程监控方法(MSPC)在工业界以及学术界都受到广泛关注，并取得了成功应用［1-3］.主元分析方法(PCA)是经典的数据降维及特征提取方法，较早被引入过程监控领域并取得了广泛应用［1，4］.然而，由于实际生产过程中采集的监控数据情况复杂，变量间不仅存在着较为明显的互相关性，且存在强自相关性.为此，有学者提出动态主元分析方法(DPCA)，以解决传统统计过程监控方法的不足［5］.然而，DPCA有2方面缺陷:首先，PCA假设噪声方差最小并且噪声各向同性，约束条件较为严格;其次，对数据矩阵采用自回归方法予以扩展，将变量的时滞测量值纳入增广矩阵，虽可以解决采样数据强序列相关性的问题，但亦增加了不必要的计算量.

因此，很多学者也在不断尝试新的动态生产过程监控方法.文献［6］指出主元分析为因子分析方法(FA)的一种特殊表现形式，并将FA引入过程监控领域.其不要求噪声方差最小以及噪声各向同性，克服了传统的PCA等方法的限制，更能反映数据的本质特征，故监控效果更为理想.文献［7］将动态主元分析思想与因子分析方法相结合，提出一种DFA过程监控方法.然而其也采用传统的数据扩展方法，并未详细分析工业过程各变量间的自相关程度，仅令各采样时刻的过程变量以及滞后d的历史数据共同组成待解变量矩阵.但是，各变量间具有不同的自相关关系，采用相同的时滞长度有时不能完全反映实际过程的动态关系，也有可能引入多余的动态关系从而增加计算量.

本文针对已有动态过程监控方法的缺陷提出了解决方案.通过自相关分析，对不同变量计算不同的时滞长度，按此方法完成增广矩阵的扩展后，再对时滞长度较长的变量进行简化处理，从而完成对不必要的动态关系的剔除［8-9］.将基于此思想的简化动态因子分析(simplified DFA)监控方法应用于TE过程，并与DPCA和DFA等方法进行对比，验证了此改进方法的有效性和优越性.

1 SDFA模型及过程监控方法

1.1 时滞确定方法

传统动态过程监控方法一般通过AR方式扩展增广矩阵，时滞长度通过引入静态关系数进行选择［10］.本文改进并简化了传统的时滞长度确定方法，新方法通过以下2步计算确定增广矩阵.

步骤1 通过相关性分析方法计算各变量自相关系数ρi(τ)，其中i为变量，τ为变化的时滞.依据相关性的性质以及过程监控对于动态性的要求，设置一个合理的阈值ρ.

①令τ=0，若ρi(τ)≤ρ，则第i个变量不需要扩展时滞;②不满足条件①的第j变量继续计算ρj(τ)，若ρj(τ)≤ρ，则第j变量时滞为1;③依此类推，直至所有变量均取得合适的时滞长度.扩展后的过程采样数据矩阵为如式(1)所示，其中(dk，…，dl)为各个变量可能取的时滞长度，而D为(dk，…，dl)中的最大值，N为扩展后变量总数.

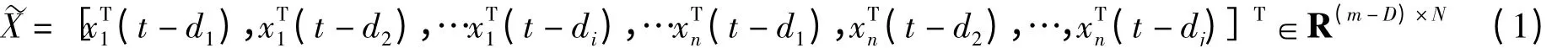
步骤2 对上述增广矩阵~X进行简化处理.若第i个变量的时滞为0、1或者2，则第i个变量的增扩数据无需简化;若第j变量的时滞为dk且3≤dk，则第j变量只考虑第k与第k－dk两时刻的相关性，即只将此两时刻的采样值纳入增广矩阵，而忽略中间时刻的值，简化后的增广矩阵如式(2)所示，M为时滞简化后变量总数.

经过上述方法处理后，(dk，…，dl)为变量时滞长度集合，其值域为{0，1，2}，可以作为观测数据，带入下一步的建模.

1.2 动态因子分析建模

动态因子分析模型的矩阵形式为

因子的联合概率密度函数为

观测数据关于因子的条件分布为

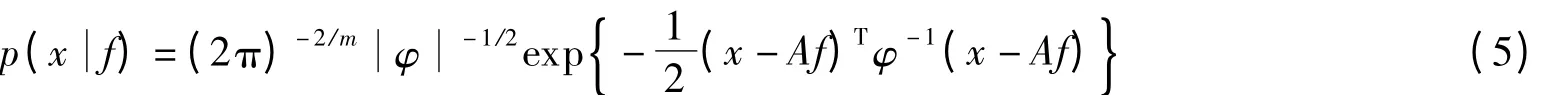
根据条件分布律，观测数据概率密度函数为

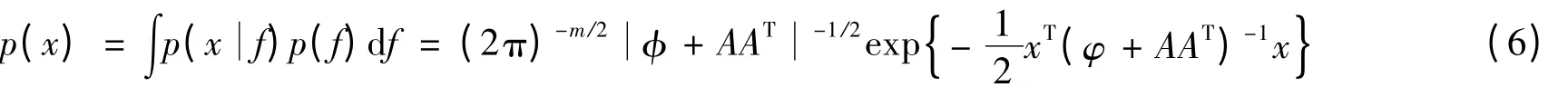
由贝叶斯定理可推得因子后验概率密度函数为

根据生成模型x～Ν(0，AAT+φ)，确定A及φ这2个参数，即可确定观测数据的分布函数.应用EM算法，迭代计算如式(8)、式(9)直至收敛，即可完成参数求解，从而完成simplified DFA模型的建立［11-12］.

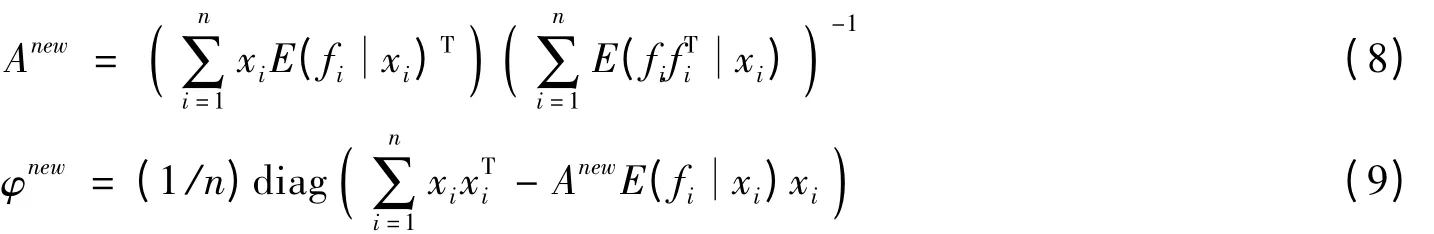
1.3 因子个数及监控指标

因子个数的确定至关重要，其选取方法有很多，如基于因子对原始信息解释率收敛及交叉检验法等，本文沿用文献［13］采用的基于Kaiser准则的选取方法.

正常工况下，因子、噪声以及变量均假定服从高斯分布，而根据该统计学理论，变量满足多元高斯分布，则变量白化值的Euclidean范数也满足一定概率分布.基于此，可以设立监控指标如下:

2)噪声空间的监控指标:反映过程变量与模型的拟合程度.根据式(3)，可推得公式:

进一步推导式(12)可得

则噪声空间监控指标为

3)综合监控指标:为减少监控工作量，同时又不失对过程监控的准确程度，鉴于对因子与噪声均采用马氏距离进行度量，可以将二者相结合，构造综合监控指标ST，直接对过程测量值进行检测［6］:

由式(10)～(15)可知，过程正常运行状况下，3种监控指标均应满足置信度为1－α、自由度不同的χ2分布.

2 仿真研究

田纳西-伊斯曼(Tennessee-Eastman)过程由美国伊斯曼化学品公司创建，其目的是为评价过程控制和监控方法提供的一个平台.其数据具有时变、强耦合等特点，包括5个主要的反应单元:反应器、冷凝器、压缩机、分离器和汽提塔，整个过程包含了12个控制变量、41个过程变量.

仿真过程数据每隔3 min采样一次，仿真时间为48 h，通过22次不同运行状况(包含正常情况与21种不同的故障情况)的仿真构成，故障均在第160个采样点引入.对TE过程的详细描述及各种故障形式的介绍参加文献［1］，工艺流程图如图1所示.

图1 田纳西-伊斯曼过程的工艺流程图

漏检率及故障检测延迟是评估故障诊断和过程监控方法优良的2个重要指标，反映了监控方法的灵敏性与鲁棒性.TE过程中21种故障的漏检率和故障检测时延的对比(DPCA与simplified DFA)如表1和表2所示.表中，除了TE过程极难检测的故障3、9、15以外，2种监控方法均可以对其他故障给予报警.可以发现，simplified DFA的监控结果优于DFA，且综合监控指标ST具有非常明显的优势.

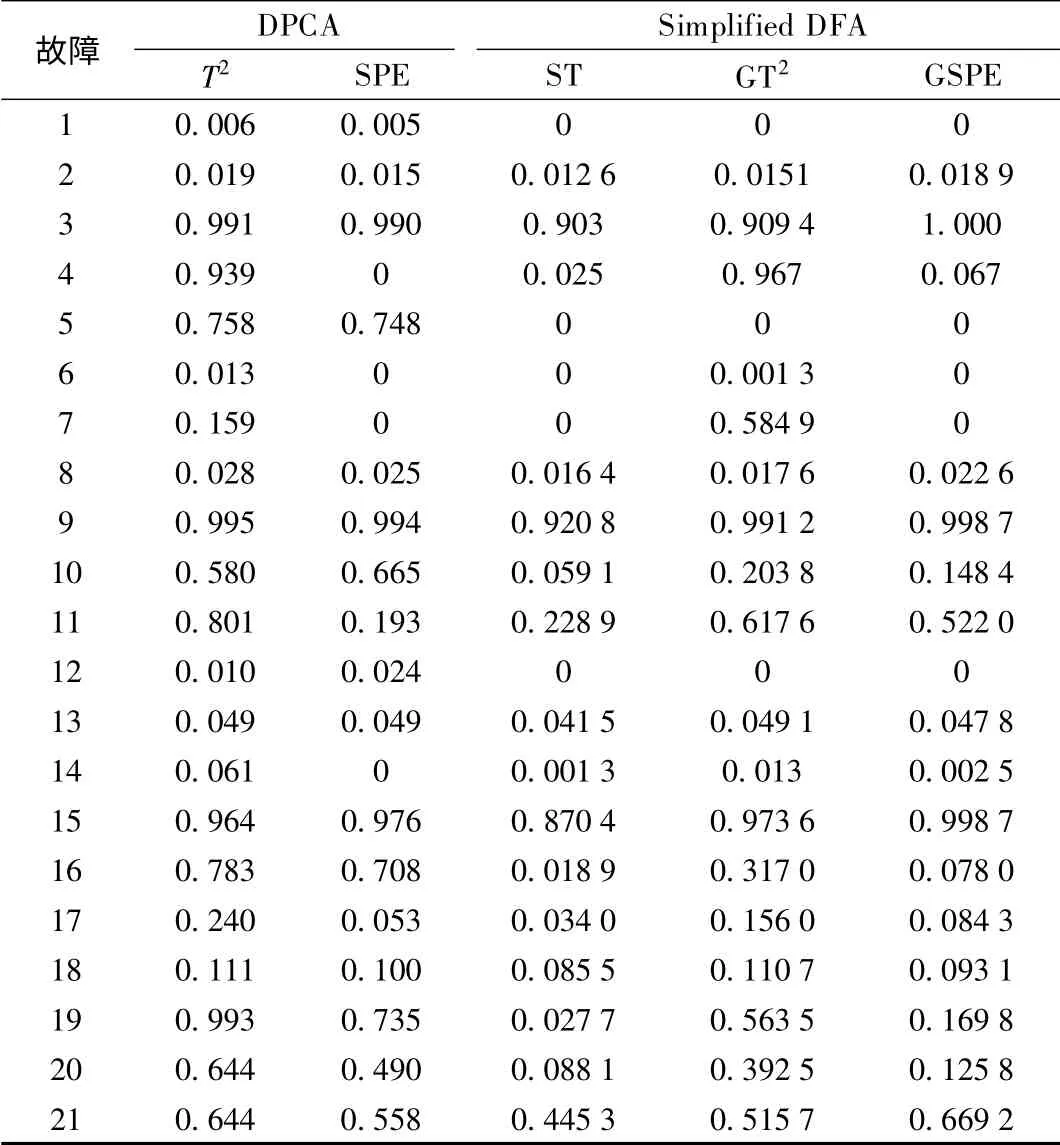
表1 漏检率

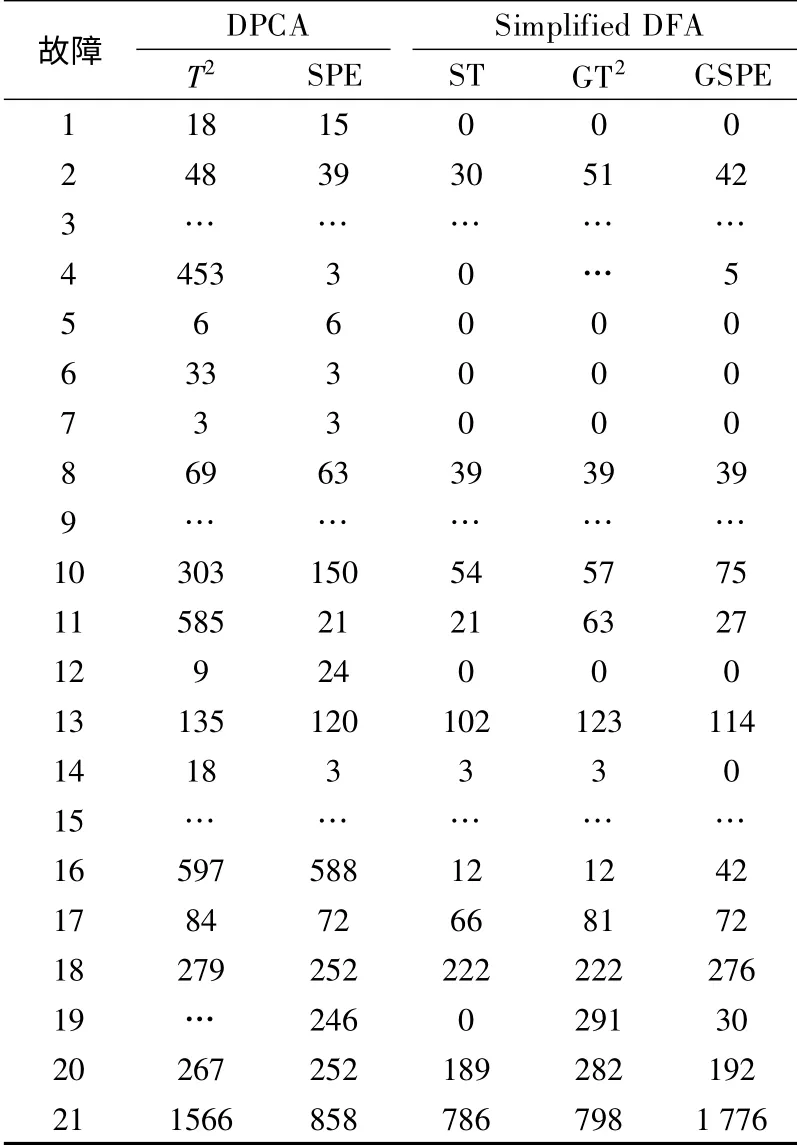
表2 检测时延

同时以故障5为例，通过监控图、漏检率及检测时延等3项指标对比DFA以及simplified DFA两种方法的监控结果.

文献［7］提出的DFA监控方法，其采用正常数据建模，时滞长度确定为2，扩展后的数据矩阵为R958×156，因子个数选择为45，采用99%的置信限，建立DFA模型，所得监控图如图2所示.本文所述的simplified DFA监控方法，采用正常数据建模，根据相关性分析，各变量时滞长度确定为0至6不等，扩展后的数据矩阵为R954×117，然后再进行简化，最终确定矩阵为R954×86.与现有动态方法相比，简化方法的一大优点就是扩展矩阵维数更低，可以有效减少计算量.因子个数选择为28，采用99%的置信限，建立simplified DFA模型，所得监控图如图3所示.

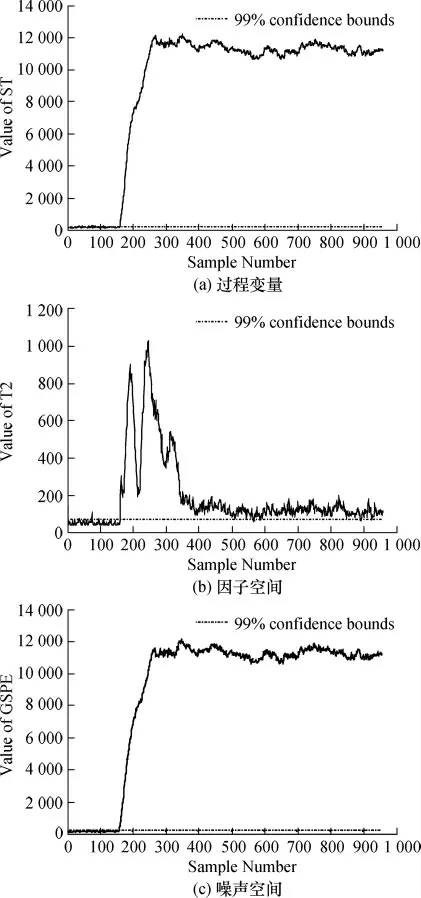
图2 基于DFA模型的监控图

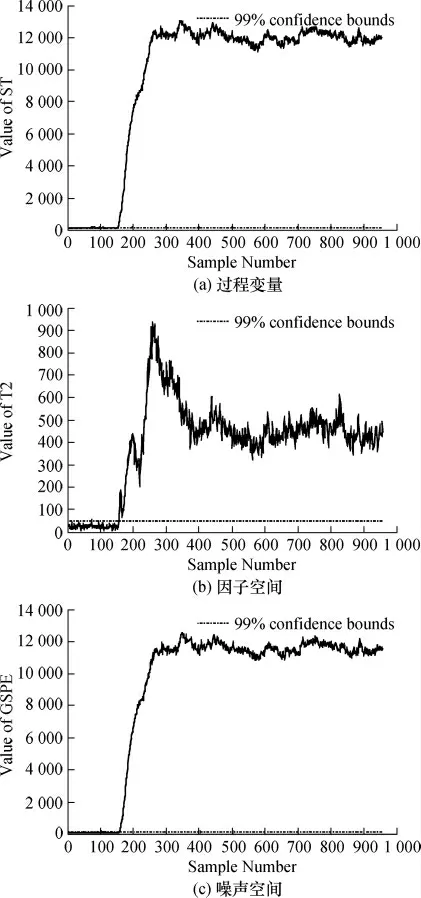
图3 基于SDFA模型的监控图

2种方法的漏检率及检测时延如表3和表4所示.

表3 漏检率

表4 检测时延

通过对比2种不同方法的监控图可以发现，2种监控方法均可以比较及时地检测到故障发生，但基于simplified DFA方法的GT2指标的监控效果略好于DFA方法.基于simplified DFA方法的GT2指标漏检率更低，且故障发生后，指标值超出控制限时更为明显，持续时间更久.

3 结语

本文针对传统多变量动态过程时滞长度确定方法存在的不足，提出了一种新的解决方案.通过对数据进行自相关性分析，针对不同变量选取不同动态时滞长度，并对过于冗长的增广数据变量进行简化处理，避免了不必要动态关系的引入，减少了数据处理量，并确保了强自相关性的体现.将这一思想与因子分析方法相结合，提出了simplified DFA监控方法.TE过程的仿真结果验证了改进方法的有效性，降低漏检率，减少了检测时延，达到了有效监控工况运行，提高动态分析性能的目的.

References)

［1］Chiang L H，Russell E L，Braatz R D.Fault detection and diagnosis in industrial systems［M］.London:Springer-Verlag，2001.

［2］Gao Xiang，Liu Fei.Dynamic process monitoring method based on recursive generalized eigenvalue decomposition using temporal covariance matrix［C］//Proceedings of the 7th World Congress on Intelligent Control and Automation.Chongqing，2008:5134-5136.

［3］Liang Jun，Qian Jixin.Multivariate statistical process monitoring and control:recent development and applications to chemical industry［J］.Chinese Journal of Chemical Engineering，2003，11(2):191-203.

［4］Lu N，Gao F，Yang Y，et al.PCA-based modeling and on-line monitoring strategy for uneven-length batch processes［J］.Industrial and Engineering Chemistry Research，2004，43(13):3343-3352.

［5］Ku W，Storer R H，Georgakis C.Disturbance detection and isolation by dynamic principal component analysis［J］.Chemometrics and Intelligent Laboratory Systems，1995，30(1):179-196.

［6］赵忠盖，刘飞.因子分析及其在过程监控中的应用［J］.化工学报，2007，58(4):970-974.

Zhao Zhonggai，Liu Fei.Factor analysis and its application in process monitoring［J］.Journal of Chemical Industry and Engineering，2007，58(4):970-974.(in Chinese)

［7］赵忠盖，刘飞.动态因子分析模型及其在过程监控中的应用［J］.化工学报，2009，60(1):183-186.

Zhao Zhonggai，Liu Fei.Modeling using dynamic factor analysis and its application in process monitoring［J］.Journal of Chemical Industry and Engineering，2009，60(1):183-186.(in Chinese)

［8］刘育明，梁军，钱积新.工业流化床反应器结块监视的动态PCA方法［J］.化工学报，2004，55(9):1546-1549.

Liu Yuming，Liang Jun，Qian Jixin:Dynamic principal component analysis method for chunk monitoring of industrial fluidized-bed reactor［J］.Journal of Chemical Industry and Engineering，2004，55(9):1546-1549.(in Chinese)

［9］边幅强，高翔.一种简化的动态独立元分析方法［J］.吉林化工学院学报，2008，25(1):49-52.

Bian Fuqiang，Gao Xiang.A simplified dynamic independent component analysis［J］.Journal of Jilin Institute of Chemical Technology，2008，25(1):49-52.(in Chinese)

［10］Michael E T.Probabilistic principle component analysis［J］.Journal of the Royal Statistical Society，1999，3(1):71-86.

［11］Rubin D，Thayer D.EM algorithms for ML factor analysis［J］.Psychometrika，1982，47(1):69-76.

［12］Ghahramani Z，Hinton G E.The EM algorithm for mixtures of factor analyzers，RG-TR-96-1［R］.Toronto:Department of Computer Science of University of Toronto，1996.

［13］尹雪岩，刘飞.FA监控方法的改进及其应用［C］//2009中国过程系统工程年会暨第四届中国MES年会会议论文集.杭州，2009:131-134.