一种融合无时滞测量值和含时滞测量值的状态估计方法

王金萍，赵忠盖，刘飞（江南大学轻工过程先进控制教育部重点实验室，江苏 无锡 214122）



一种融合无时滞测量值和含时滞测量值的状态估计方法

王金萍，赵忠盖，刘飞
（江南大学轻工过程先进控制教育部重点实验室，江苏 无锡 214122）

摘要：在很多工业过程中，常常可获得两种测量数据，无时滞测量值和含时滞测量值，其中，无时滞测量值直接由传感器在线测得，即时却精度较低，含时滞测量值通过人工实验分析离线得到，精度高却有时滞。引入状态增广卡尔曼滤波法对上述两种数据进行融合以估计当前状态值。考虑到无时滞测量值建立的在线软测量模型存在不可避免的模型不匹配问题，引入模型偏差作为待估计状态，通过离线测量值对其进行估计，从而实现对在线软测量模型的校正。最后将所提方法运用到线性化的非线性二元蒸馏塔模型中估计填料压板各成分浓度，取得了良好效果。

关键词：时滞；状态增广卡尔曼滤波；测量模型；校正；蒸馏塔

2015-12-11收到初稿，2015-12-21收到修改稿。

联系人：赵忠盖。第一作者：王金萍（1989—），女，硕士研究生。

引 言

很多工业过程中，通常可获得在线测量值和离线测量值。在不同工业过程中，在线测量值和离线测量值所代表的意义、精度和实时性也不同。在线测量值可分为两种，直接在线测量值，如常规变量流量、液位等，和可通过间接计算得到的变量，即间接在线测量值，如浓度或成分，直接测量会有些困难，可以通过在线分析仪进行测量，但是会有一定时间的滞后，还可以通过测量温度、流量等间接变量，建立软测量模型，计算得到所需要测量的变量[1-3]。本文所指在线测量值即为无时滞的间接在线测量值，通过建立软测量模型计算得到所需要测量的变量。这类在线测量值由传感器检测得到，有规律、采样周期小且无时滞，但是测量精度较低。离线测量值无法由传感器直接检测，需要通过人工检测分析得到，无规律、采样周期大且含时滞，测量精度较高。例如，在蒸馏塔中，蒸馏物和底物的成分经常需要实验分析才能得到，而填料压板的温度则可以通过传感器直接测量得到[4-5]。虽然蒸馏物和底物的成分也可以通过填料压板的温度间接估计，但估计值通常会受到模型误差、传感器偏差或者非模型干扰等问题的影响，得到的估计值效果不好，而离线分析得到的测量值更为准确但含有滞后，主要由采样产生的时间滞后与人工检测分析产生的化验滞后组成。在这种情况下，针对两种测量值进行融合以得到精确度更高的状态值已成为焦点问题。在工业过程中，常常存在无法在线测量的关键变量，可以建立软测量模型利用一些可直接测量的辅助变量进行计算。卡尔曼滤波法已成为现今工业过程中应用最广泛的状态估计方法[6]，然而，简单的卡尔曼滤波器公式只能应用于没有延时的标准系统。

对于含滞后的测量值，Alexander[7]提出了一种序列化处理时滞测量值的方法，该方法利用滞后测量值对滤波器的估计进行修正，Larsen等[8]对上述方法进行了扩展与延伸，该方法可以解决采样的滞后测量值测量误差协方差不确定的情况。含滞后的多采样率估计值也经常会用状态增广来处理。Gudi 等[9-10]在发酵过程的生物反应器中应用了带延迟测量值的多采样率状态估计技术。在过程系统中，状态增广卡尔曼滤波算法[11]只是进行了简单的状态增广，增益矩阵进行相应改变，即可转换为标准的状态空间模型，实现比较简单。

但是，软测量模型存在不可避免的模型不匹配，即存在模型偏差，需要对在线软测量模型进行校正[12]。Shao等[13]和Deng等[14]分别介绍了用贝叶斯方法和期望最大化法对模型参数进行校正，彭小奇等[15]提出构建软测量模型性能评价指标来判断是否需要校正并根据情况进行自适应校正，但是这类方法仅能用于无延时模型的校正。

本文考虑离线采样间隔存在无规律性，首先利用状态增广卡尔曼滤波算法将无时滞测量值与含时滞测量值进行融合，估计当前状态值，并在状态增广卡尔曼滤波算法的基础上，在离线测量值到达后对在线软测量模型进行校正，得到更为精确的软测量模型，以降低模型不匹配对估计值的不利影响。

1 状态估计问题描述

本章节首先对离散线性系统的标准卡尔曼滤波器进行描述，然后对含有在线测量值和含滞后的离线测量值的状态空间模型进行描述及分析。

1.1 标准卡尔曼滤波

离散线性系统的状态空间模型如下

式中，Pk、Kk分别为状态误差协方差和卡尔曼滤波增益。

1.2 含滞后状态空间模型

图1 含时滞测量值的系统Fig.1 System with measurements with time delay

在线测量值与含滞后离线测量值测量时间与测量到达时间的关系如图1所示。其中，k为当前测量时间，表示在线测量值，表示离线测量值，，s表示离线采样时间。在线测量值没有滞后且采样周期小，使用垂直箭头表示。离线测量值在s时刻采样后，需进行人工实验分析，化验结果经过ds个采样间隔才能获得，使用虚线箭头表示，且离线测量值的采样周期大，在s时刻采样后，下一个采样点为s+ ms，ms为两个离线采样点的间隔数量。由于离线采样不规律，即ms为不定值，且采样之后要经过人工实验分析才能得到，即ds也为不定值。通常只有在线测量值的时刻称为次要时刻，在线测量值与离线测量值同时到达的时刻称为主要时刻[4]。

由图1中测量时间与测量达到时间的关系，可以得到含时滞测量值的状态空间模型

由于模型中含有时滞，无法直接利用式（3）～式（7）进行计算，而状态增广卡尔曼算法则可通过对状态的增广，将模型式（8）～式（10）转化成模型式（1）～式（2）的形式，即可直接利用式（3）～式（7）进行计算，估计出当前状态值，方法简便，应用性强。

2 含时滞的状态估计

本文进行含时滞的状态估计所用方法为状态增广卡尔曼滤波算法。滞后的离线测量值不仅影响着它本身采样点s时刻的状态估计值，还影响了s时刻之后一直到s+ ds时刻的状态估计值，将离线测量值到达时的状态设为当前时刻和过去ds个状态的增广，状态增广向量为

增广状态空间模型为

其中

上述状态空间模型已经转换为标准的状态空间模型，可以直接用卡尔曼滤波公式[式（3）～式（7）]进行状态估计，可以得到估计值为

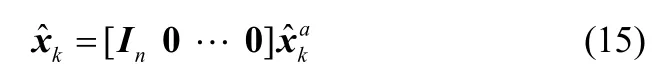
实际操作中，离线测量值是需要经过人工实验分析才能得到，操作时间具有不确定性，即离线测量值的滞后时间不确定，采用可能产生的最大滞后时间dmax来对系统进行增广，而一旦测量值得到之后ds也就确定了，，测量方程也能随之作相应调整。本方法最大优点为，将状态矩阵及其他增益矩阵做了相应增广之后就能使用标准的卡尔曼公式进行计算。

3 在线模型校正

本章节描述因在线软测量模型所存在的不可避免的模型误差对状态估计值的不利影响，本文提出利用离线测量值对在线软测量模型进行校正的方法。

3.1 在线模型校正的必要性

在工业过程中，常常存在一些无法用传感器直接测得的变量，如某种物质的浓度或组成，因此需要借助一些传感器可直接测量的变量，即辅助变量，如温度、压力、流量、溶氧量或pH等，通过建立相对应的软测量模型来间接获得。然而，所建立的软测量模型会存在无法避免的模型误差，且会随着生产过程的进行而不断发生变化，下面通过一个简单示例展示一下当存在模型误差时，所得到估计状态的结果。

有状态空间模型如下

模型偏差未知，进行状态估计时仍然采用模型(16)，从而得到状态真实值与估计值结果如图2所示。

从图2可以看出，模型偏差的存在，使所求状态真实值与估计值之间的差距逐渐加大，需要对软测量模型进行适时的校正，以得到更好的估计结果。

3.2 在线模型校正

由3.1节可知，为降低因模型偏差所带来的不利影响，需要对在线模型进行适时的校正，而在本文所介绍的模型中，校正所包含的测量信息包括在线测量值和离线实验分析数据。而离线分析数据的准确性更高，当离线实验分析数据得到之后，再对在线软测量模型进行校正。模型偏差项bk未知且不断变化，也作为待估计的状态出现，且只有当离线实验分析数据到达之后再对bk进行校正，bk只有在到达的时刻才作为待估计的状态出现，而在只有在线测量值的时候作为常量进行计算，在线模型校正与离线数据滞后并存的状态空间模型如式（18）～式（21）

图2 模型存在偏差时的估计效果Fig.2 Estimation effects when model has deviation

其状态空间模型如下

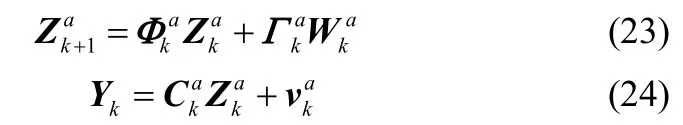
其中

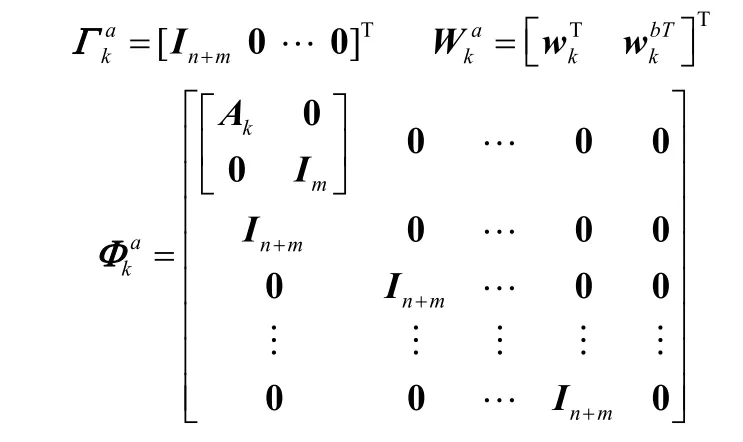
然而，离线测量值带有一定的滞后，bk能否可观测到仍存有疑问，因此首先需要对系统的能观性进行判断，如系统完全可观，即xk与bk均可观，则可对在线测量模型进行校正，否则将无法进行校正。

对标准模型即式（1）、式（2），x完全能观的充要条件是nm×n矩阵

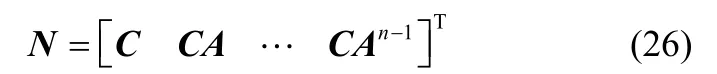
的秩为n[17]，N为能观性矩阵。

对在线模型较真与离线数据滞后并存的状态空间模型，即式（18）～式（21），其变换后的标准状态空间模型为式（23）～式（24），，完全能观的充要条件为[(n+ m )×1矩阵

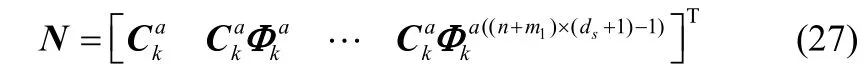
若

4 实例仿真

在这部分，将引用两个例子来说明本文介绍方法的优点，一个是对3.1节中所介绍的模型进行校正后的估计效果，另一个是采用线性化的非线性二元蒸馏塔模型[2]。蒸馏塔模型分为两种情况进行仿真，一种是不考虑模型偏差，直接利用状态增广卡尔曼滤波法进行估计，另一种是考虑模型偏差，对在线模型进行校正。

4.1 数字算例仿真

由3.1节可以知道，模型偏差的存在，状态真实值与估计值间的差距较大，现采用3.2节中所介绍的方法对在线模型进行校正，引入模型偏差bk，其噪声的协方差Qb较大，设定为Qb= I，校正后的估计效果如图3所示。

由图3可以看出，校正后的估计值更加接近真实值，校正后估计效果改善较多。通常可以采用均方根误差值(RMSE)来评判方法的有效性。无校正与校正后估计值与真实值的均方根误差值分别为RMSE1和RMSE2，如表1所示。由表1可以更客观地看出利用离线测量值对在线测量模型进行校正后估计效果更加良好。

4.2 蒸馏塔模型仿真

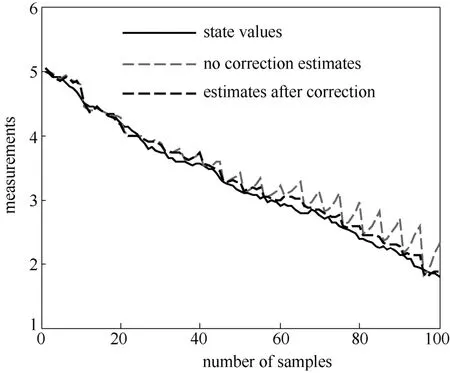
图3 模型校正后的估计效果Fig.3 Estimation effects after online model is corrected

表1 在线模型无校正与有校正的RMSE值Table 1 RMSE values of online model with no correctionand after correction

图4 多采样率数据状态估计Fig.4 State estimations with multiple sampling rates

首先只考虑不需要进行校正的情况，这时有两种情况，即只有在线检测值进行估计及考虑在线检测值、含滞后的离线分析数据共同作用的情况。假设样本总数为100，而离线采样点间隔为ms=6，滞后时间ds=5，其仿真效果如图4所示。

由图4可看出，当只有在线测量值时，估计值在30个样本点之后才接近真实值，而明显地，在线测量值和含滞后的离线分析值共同作用时，估计值会更快地接近真实值。

同样采用RMSE来评判所采用方法的有效性。RMSE3表示只有在线测量值进行估计时，估计值与真实值之间的均方根误差，RMSE4表示在线测量值与离线分析值共同估计时估计值与真实值之间的均方根误差。根据采样间隔和滞后时间的不同，分为3组进行比较，分别是，、和、，其RMSE如表2所示。

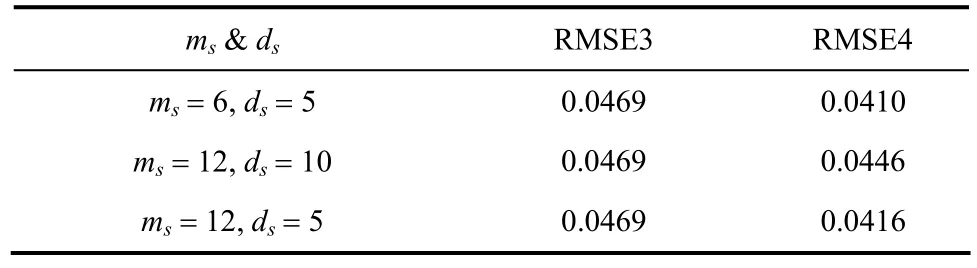
表2 多采样率状态估计RMSE值Table 2 RMSE values of state estimation with multiple sampling rates

由表2可以看出，使用更为精确的离线分析值进行估计显然比只有在线测量值估计的效果要好，而采样间隔和滞后时间越小，估计结果越好，且采样间隔对估计结果的影响比滞后时间对估计结果的影响要小。

现在来考虑需要校正的情况。首先应判断xk与是否可观测，由式（30）～式（32）可知，n =4，，假定则根据式（27）可计算出能观性矩阵N（由于空间问题，此处简略），经判断，N的秩为36，xk与bk是可观测的，可以对在线模型进行校正。

利用3.2节中所述校正方法进行校正，此时，偏差项bk的噪声的协方差较大，设定为Qb= I，仿真结果如图5所示。由图5可以看出，当没有进行校正时，估计值会逐渐偏离真实值，进行校正后，估计值会基本接近真实值。

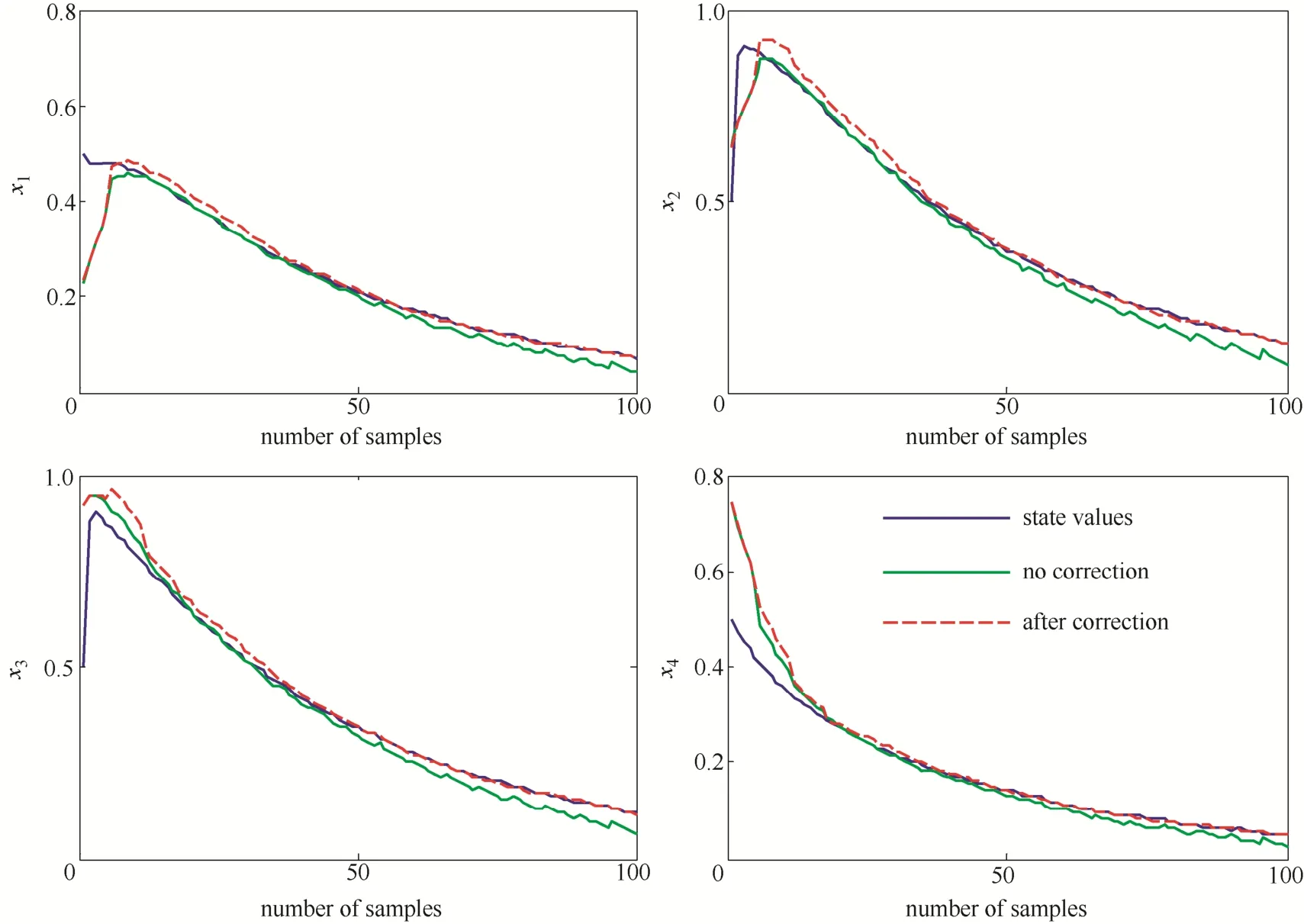
图5 带校正多采样率状态估计Fig.5 State estimations with multiple sampling rates after correction

同样用RMSE来评判校正的效果，并采用3组不同的采样间隔和滞后时间进行比较，RMSE5和RMSE6分别表示无校正和有校正的均方根误差。其RMSE如表3所示。由表3可知，校正后的效果明显比没有校正的效果好，但相比于表2可知，由于不是每时每刻都在校正，其相应的RMSE要比没有偏差的时候稍大。其采样间隔和滞后时间对RMSE的影响同上述不需要进行校正的情况相同，在此不多赘述。

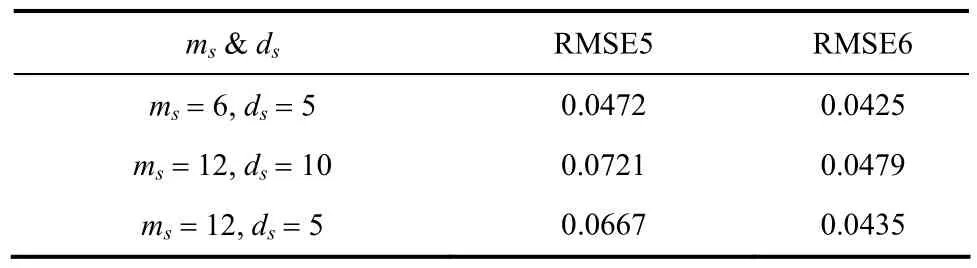
表3 带校正多采样率状态估计RMSE值Table 3 RMSE values of state estimation with multiple sampling rates after correction

离线测量值不仅含有时滞，其采样也无规律，采样周期远大于在线测量值。离线取样由操作人员手工完成，其采样间隔受操作人员的经验知识和过程的运行状况决定。在有些运行阶段，过程状态变化小，离线取样间隔往往较大，而在过程状态变化较大的阶段，取样周期通常较小。此外，不同操作人员的经验知识存在差异，他们对过程运行状态判断有所不同。但是本文提出的算法考虑分有离线采样数据和无离线采样数据两种情况设计，离线取样的间隔仅对估计结果存在影响，采样间隔小的时段估计结果较好，采样间隔大的时段估计结果较差。

5 结 论

本文描述了利用状态增广卡尔曼滤波法对在线测量值和离线测量值进行状态估计的方法，其中在线测量值为有规律、采样周期小且无时滞的，离线测量值为无规律、采样周期大且含有一定时滞的，并由于模型建立的不匹配及生产过程中产生的模型偏差会对状态的估计有不利影响，利用离线测量值对在线软测量模型进行校正。通过对蒸馏塔模型的仿真验证了所采用方法的有效性，并根据采样间隔和滞后时间不同所进行的仿真结果比较得知，采样间隔和滞后时间越小，估计和校正效果越好，且采样间隔对估计结果的影响比滞后时间对估计和校正效果的影响要小。

References

[1] 黄道平, 刘乙奇, 李艳. 软测量在污水处理过程中的研究与应用[J]. 化工学报, 2011, 62 (1): 1-9.

HUANG D P, LIU Y Q, LI Y. Soft sensor research and its application in wastewater treatment [J]. CIESC Journal, 2011, 62 (1): 1-9.

[2] 陈定三, 杨慧中. 基于局部重构融合流形聚类的多模型软测量建模 [J]. 化工学报, 2011, 62 (8): 2281-2286. DOI: 10.3969/j.issn.0438-1157.2011.08.034.

CHEN D S, YANG H Z. Multiple model soft sensor based local reconstruction and fusion manifold clustering [J]. CIESC Journal, 2011, 62 (8): 2281-2286. DOI: 10.3969/j.issn.0438-1157.2011.08.034.

[3] 李修亮, 苏宏业, 褚健. 基于在线聚类的多模型软测量建模方法[J]. 化工学报, 2007, 58 (11): 2834-3838.

LI X L, SU H Y, CHU J. Multiple models soft-sensing technique based on online clustering arithmetic [J]. Journal of Chemical Industry and Engineering (China), 2007, 58 (11): 2834-3838.

[4] GOPALAKRISHNAN A, KAISARE N S, NARASIMHAN S. Incorporating delayed and infrequent measurements in extended Kalman filter based nonlinear state estimation [J]. Journal of Process Control, 2011, 21 (1): 119-129.

[5] GUO Y, ZHAO Y, HUANG B. Development of soft sensor by incorporating the delayed infrequent and irregular measurements [J]. Journal of Process Control, 2014, 24 (11): 1733-1739.

[6] KALMAN R E. A new approach to linear filtering and prediction problems [J]. Journal of Fluids Engineering, 1960, 82 (1): 35-45.

[7] ALEXANDER H L. State estimation for distributed systems with sensing delay[C]//Orlando '91. Orlando, FL: International Society for Optics and Photonics, 1991.

[8] LARSEN T D, ANDERSEN N A, RAVN O, et al. Incorporation of time delayed measurements in a discrete-time Kalman filter[C]// Proceedings of the 37th IEEE Conference on Decision & Control. 1998: 3972-3977.

[9] GUDI R D, SHAH S L, GRAY M R. Multirate state and parameter estimation in an antibiotic fermentation with delayed measurements [J]. Biotechnology and Bioengineering, 1994, 44 (11): 1271-1278.

[10] GUDI R D, SHAH S L, GRAY M R. Adaptive multirate state and parameter estimation strategies with application to a bioreactor [J]. AIChE Journal, 1995, 41 (11): 2451-2464.

[11] GELB A. Applied optimal estimation [J]. Proceedings of the IEEE, 1976, 64 (4): 574-575.

[12] KADLEC P, GRBIC R, GABRYS B. Review of adaptation mechanisms for data-driven soft sensors [J]. Computers & Chemical Engineering, 2011, 35 (1): 1-24.

[13] SHAO X, HUANG B, LEE J M, et al. Bayesian method for multirate data synthesis and model calibration [J]. AIChE Journal, 2011, 57 (6): 1514-1525.

[14] DENG J, XIE L, CHEN L, et al. Development and industrial application of soft sensors with on-line Bayesian model updating strategy [J]. Journal of Process Control, 2013, 23 (3): 317-325.

[15] 彭小奇, 孙元, 唐英. 一种软测量模型性能检测评价及其自适应校正方法 [J]. 化工学报, 2012, 63 (5): 1474-1483. DOI: 10.3969/ j.issn.0438-1157.2012.05.022.

PENG X Q, SUN Y, TANG Y. Performance monitoring and assessment of a soft-sensor and its adaptive correction [J]. CIESC Journal, 2012, 63 (5): 1474-1483. DOI: 10.3969/j.issn.0438-1157.2012.05.022.

[16] MERWE R, WAN E. Sigma-point Kalman filters for probabilistic inference in dynamic state-space models[C]//Proceedings of the Workshop on Advances in Machine Learning. 2003.

[17] 刘豹, 唐万生. 现代控制理论 [M]. 第3版. 北京: 机械工业出版社, 2006: 106-110.

LIU B, TANG W S. Modern Control Theory [M]. 3rd ed. Beijing: China Machine Press, 2006: 106-110.

研究论文

Received date: 2015-12-11.

Foundation item: supported by the National Natural Science Foundation of China (61573169, 61134007).

State estimation approach by incorporating measurements with delay-free and time delay

WANG Jinping, ZHAO Zhonggai, LIU Fei
(Key Laboratory of Advanced Process Control for Light Industry, Ministry of Education, Jiangnan University, Wuxi 214122, Jiangsu, China)

Abstract:In many industrial processes, in addition to the online measurements with delay-free and low inaccuracy, there exist delayed measurements accurately obtained by laboratory analysis. The augmented state Kalman filter is employed to estimate the state by incorporating both the delayed and the delay-free measurements. To overcome the model-plant mismatch of the online soft-sensor model built by the delay-free measurements, the model deviation is employed to update the soft-sensor model. To follow the model drift, the model deviation is treated as a state, and it will be estimated when the offline measurements arrive. In the end the proposed method is used to estimate the tray compositions in the linearized nonlinear binary distillation column model and obtains good results.

Key words:time delays; augmented Kalman filter; measurement model; update; distillation column

DOI：10.11949/j.issn.0438-1157.20151885

中图分类号：TN 713.3；TP 274.2

文献标志码：A

文章编号：0438—1157（2016）03—0940—07

基金项目：国家自然科学基金项目（61573169）；国家自然科学重点基金项目（61134007）。

Corresponding author:Prof. ZHAO Zhonggai, gaizihao@jiangnan.edu.cn