城际公共交通系统最短路算法

黄远春，胥耀方，潘海泽

(1.上海工程技术大学城市轨道交通学院，上海201620;2.北京交通大学交通运输学院，北京100044)

随着我国城市化建设与区域经济发展，“城际通道”的结构也不断调整与完善，逐渐形成了以铁路交通为主，公路交通为辅的网络模式。城际公共交通系统，包括铁路系统和长途客运系统，是城际通道的重要组成部分，为出行者提供了多样的出行路径。在路径选择时，出行者总是根据个人偏好选择出行路线(或希望出行费用最低，或希望换乘次数最少，或希望出行时间最少)，可称为最短路径因素。笔者针对城际公共交通网络的特点，综合考虑换乘、时间、票价等因素，提出一种基于Flord算法的最小换乘矩阵及对应路径的获取方法，并利用最小换乘路径进行站线搜索与费用计算，获取城际交通的最短路。

1 城际网络概况

城际运输网络不同于城市道路网，其主要具有线路连通性［2－3］、站点差异性、班次固定性、线路差异性等特点。在城市道路网中，某一路径的耗时为固定值，但在城际网络中，由于交通方式或线路条件的差异，即使行驶相同的路径，不同线路也会产生不同的耗时，从而形成不同的交通阻抗。

从城际网络的特点中不难发现，线路及相关信息是城际运输网络最短路中的关键因素，而由于不可能在任何一对城市之间都开行直达线路，城际交通中必须充分考虑换乘问题，杨新苗等［3］研究也表明，换乘次数最少是乘客出行考虑的首要因素。虽然该研究侧重于城市公交路网，但在城际运输网络中，如果换乘次数增加，则由此引起的不可预知的因素也会大大增加，如车辆到来的时间、路况，换乘时需要步行的距离等都会引起途中时间的延长［4］。因此，换乘导致的出行时间增加和旅行舒适性的降低，将会严重影响乘客对出行方式的选择。所以，本算法将以换乘次数最小为首要目标，时间与票价综合费用最小作为为第2目标，来获取城际运输的最短路。

很多学者研究了基于换乘次数最小的最短路算法，张林峰等［5］于2003年利用图论对公交网络进行分析，通过对换乘矩阵的迭代，获取最小换乘矩阵;王莉等［6］于2004年引入直达矩阵和最小换乘矩阵的算法，讨论公交网络节点间换乘问题，得出最少换乘算法。以上2种方法通过建立最小换乘矩阵来获取OD点之间的最小换乘次数，虽然能够较快地获取最小换乘矩阵，但必须重新搜索路径，并且无法体现最小换乘次数受到已成生换乘次数的影响，导致最终换乘次数可能超过要求的最小换乘次数。针对此问题，翁敏等［7］于2004年采用结点－弧段－有向线的方法，以线路，站点为基础，对公交网络的数据重新组织，研究了以最小换乘次数为首要目标的出行路径选择模型;廖楚江等［8］利用武汉市数据对这种线路站点算法进行计算机实现，但对系统提出了较高要求。由此可见，以线路站点为基础获取最小换乘路径的算法，虽然能够准确地捕捉最短换乘路径，但由于需要对所选线路上所有站点进行筛选而导致搜索时间较长，路网越大该缺点越为明显，并且，该算法现多用于城市公交网络，没有考虑不同线路在站点的到发时间影响。为解决搜寻最短换乘路径困难的现状，笔者基于Flord算法建立最小换乘矩阵，同时获取最小换乘路径，然后在确定的换乘站点中，搜索通行线路，最后通过比选，得到最小换乘次数下，广义费用最小的出行路径。

1.1 基于Flord的最小换乘算法

本算法以不同站点之间的可达性为权重，建立初始的可达矩阵H0与路径矩阵D0，然后通过Flord算法对H矩阵进行迭代，当发现不大于原路径换乘次数的新路径时，则更新Ht矩阵与Dt矩阵。需要说明的是，原有的Flord算法仅更新权重小于已存路径的新路径信息，该算法只能找出一条最短路，但由于城际交通网络的复杂性，存在多条满足最小换乘次数路径，因此，本算法将记录小于或等于已存路径的新路径信息，同时增加路径矩阵Dt的维数，利用其记录多个换乘次数最少的换乘站点，并通过矩阵Ct记录站点个数，记录最终获得所有满足最小换乘次数的路径。具体步骤如下:

1)初始化矩阵 H0，D0。其中换乘节点个数c0i，j=0，最小换乘次数的连通站点数d0i，j，m=j

2)更新矩阵H，D。对p=1…T，进行如下的搜索:对于所有的 i，j，若存在一点 p(t≠i，j)，使hi，p+hp，j>hi，j，则 hi，j=hi，p+hp，j，ci，j=1。

若存在一点 p(p≠i，j)，使 hi，p+hp，j=hi，j，则ci，j=ci，j+1;di，j，m=p;m=ci，j。当 p=T 时，搜索停止。

3)最小换乘矩阵。经过T次迭代，得到可达矩阵HT，即可求取最小换乘矩阵B。

4)识别最小换乘路径。对最小换乘矩阵B，可识别任意起点Ns与终点Ne之间的换乘次数，令其路径可分为以下 3类:

1)初始化。基于最小换乘矩阵B，路径矩阵DT与节点个数矩阵CT，通过Flord算法找出任意一条符合条件的最小换乘路径(当cNK+1，N0>1时，m=1)，同时初始化，mk，即 u=1;初始路径为:［1，K］;mk=1，k∈［1，K］;k=K;转2);

2)比较mk与。若，转3);若 mk，转7);

7)结束判断。若 k>1，k=k－1，转2);若 k=1，结束。

1.2 基于最小换乘路径的站点线路搜索法

由前面得到的u条最短换乘路径，分别搜索各个换乘站之间的铁路或公路线路，再将对于同一换乘路径(即换乘站点固定)不同区段的线路排列组合，得到多种线路换乘方案，最后，比较不同换乘路径不同线路换乘方案下的广义费用，取最优组合。需要说明的是，本算法将换乘次数作为了首要选择条件，第2目标选定了由票价和时间组成的广义费用，票价的时间价值换算公式如下:

于是，广义费用的目标函数如下，其中第1部分为线路运行区间票价的时间价值;第2部分为线路运行时间;第3部分为换乘需要消耗时间:

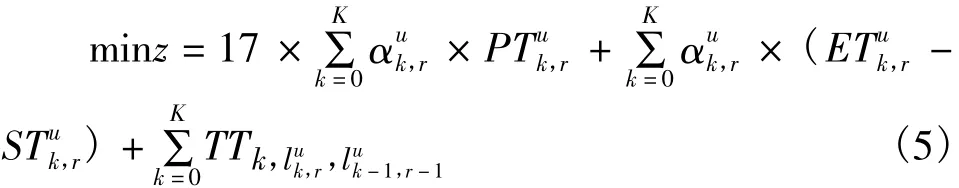
2 算例

以图1路网为例，求取Ns=1，Ne=7之间的最佳路径，各线路的票价表以及时刻表分别如表1、表2，为方便起见，假定本算例中必要换乘时间均为30 min。

易知T=7，根据不同站点之间的可达性建立D0，C0，H0，然后通过 2.1 的算法最小换乘矩阵 B，换乘节点个数矩阵CT，路径存储矩阵DT。根据本算例提取各矩阵中的数据分别如表3。

图1 城际交通路网图Fig.1 Intercity road network map

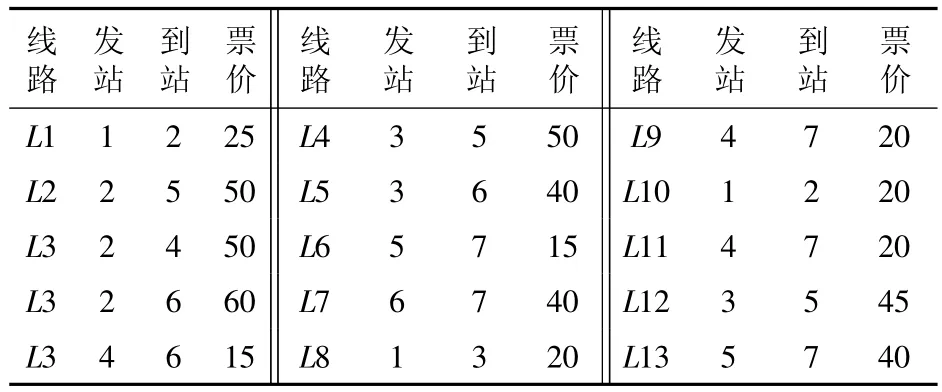
表1 各线路票价Tab.1 Fare table of each line

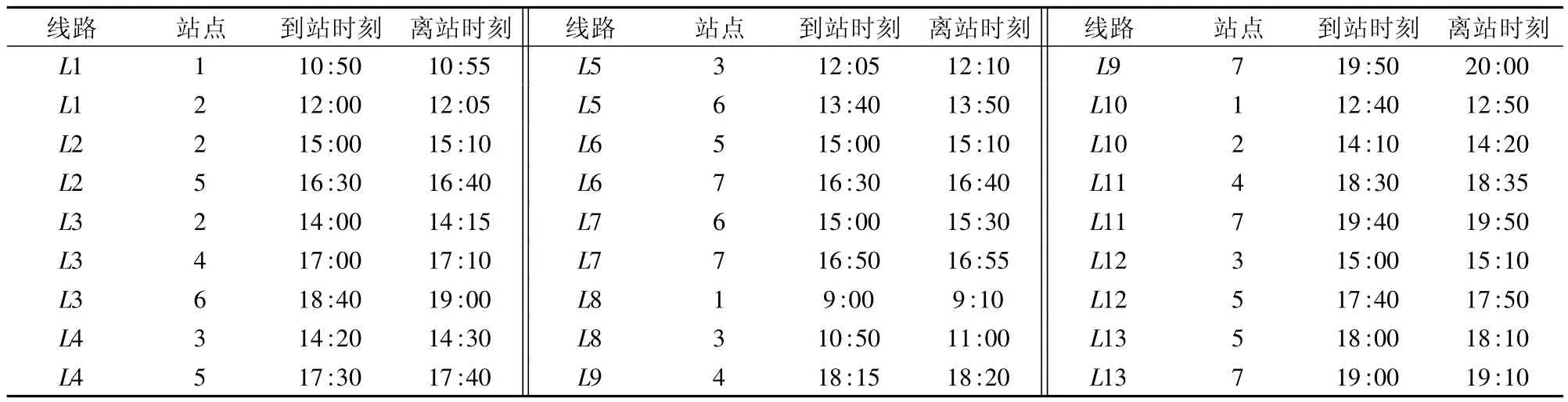
表2 各线路时刻Tab.2 Timetable of each line

表3 各矩阵中的数据值Tab.3 Timetable of each line

对矩阵进行最短路辨别，首先初始化，易知K=b1，7=2，令 m=1，u=1 使用原始的 Floyd 算法搜索在从表3中得到第一条最短换乘路径:

同时得到其它两条路径:

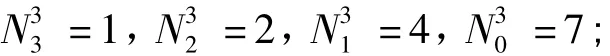
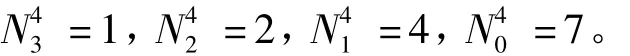
得到所有最短换乘路径之后，按照2.2的站点搜索法，得到各出行方案及广义费用如表4，因此得到最短路径为方案2。

表4 各方案线路、站点及费用Tab.4 Line，station，fare of programs

3 结论

在综合考虑换乘、时间、票价等因素的基础上，提出一种基于Floyd算法的最小换乘矩阵及对应路径的算法，并利用最小换乘路径进行站线搜索与费用计算，从而获取城际交通的最短路。该算法不仅可以准确地捕捉最小换乘路径，简化了路径搜索的过程，同时考虑了城际交通所特有的换乘时间因素，增强了算法的适用性，城际交通换乘的研究具有重要参考价值和借鉴意义。

［1］牛学勤，王炜.基于最短路搜索的多路径公交客流分配模型研究［J］. 东南大学学报:自然科学版，2002，32(6):917－919.

［2］徐业昌，李树详.基于地理信息系统的最短路径搜索算法［J］.中国图像图形学报，1998，3(1):39 －43.

［3］杨新苗，王炜，马文腾.基于GIS的公交乘客出行路径选择模型［J］.东南大学学报:自然科学版，2000，30(6):87 －91.

［4］苏啸，曾子维.基于关联的城市公交换乘查询算法［J］.计算机工程与设计，2006，27(3):519－521.

［5］张林峰，范炳全，吕智林.公交网络换乘矩阵的分析与算法［J］.系统工程，2003，21(6):92 －96.

［6］王莉，李文权.公共交通系统最佳路径算法［J］.东南大学学报:自然科学版，2004，32(4):264 －267.

［7］翁敏，毋河海，杜清运，等.基于公交网络模型的最优出行路径选择的研究［J］.武汉大学学报:信息科学版，2004，29(6):500－503.

［8］廖楚江，蔡忠亮，杜清运，等.基于最少换乘的公交最优路径算法的设计与实现［J］.武汉大学学报:信息科学版，2006，31(10):904－907.