双车道公路期望车速确定方法研究

屠书荣，张泽良

(重庆交通大学土木建筑学院，重庆400074)

期望车速是指车辆行驶过程中在不受或基本不受其他车辆约束的情况下，驾驶员心目中希望达到的最高安全行驶速度［1］。目前在公路设计阶段，已普遍采用相邻路段运行速度的差值对公路线形安全性进行评价，而期望车速是运行速度预测的关键参数，对运行速度预测和线形安全性评价的影响非常大，但我国JTG/TB 05—2004《公路项目安全性评价指南》［2］中推荐的运行速度预测方法，其期望车速的取值为小客车120 km/h，大货车75 km/h与双车道公路的实测期望车速相去甚远(对双车道公路而言，上述期望车速取值明显偏高)，这在很大程度上影响了双车道公路运行速度预测的精度。由于双车道公路与高速公路或一级公路的行车环境差异较大，在进行双车道公路运行速度预测时，有必要对其代表车型的期望车速数值进行重新确定。

1 期望车速形成过程及影响因素分析

调查发现，每个驾驶员在驾车过程中，其心目中都或明或暗地存在着一个“目标车速”，这个“目标车速”实际上就是期望车速。驾驶员对期望车速的选择首先取决于道路条件和所驾驶的车型，在这两个条件确定后，期望车速会随驾驶员的性别、年龄、气质、驾驶技术熟练程度及驾车风格等不同在一定范围内发生波动，但道路条件始终是驾驶员选择期望车速的基础和关键，不会因驾驶员个体的差异而发生改变。从心理学角度分析，驾驶员期望车速的形成过程大致可以分为初定、调整、确定和保持4个阶段(图1)。

图1 期望车速形成过程Fig.1 The process of expectation speed formation

1)初定阶段:驾驶员确定心目中期望车速的初始阶段。当驾驶员驾车驶入某一条道路时，首先获取的是道路等级状况，驾驶员会根据行驶道路的横断面尺寸和车型等要素判断后确定一个初始期望车速;

2)调整阶段:驾驶员对已经初步确认的期望车速进行调整的阶段。此阶段的特点是驾驶员通过对所行驶道路的线形及交通环境等相关情况作进一步观察后，决定是否对已确定的初始期望车速进行调整以及调整的幅度大小;

3)确定与保持阶段:驾驶员对已调整过的期望车速实施记忆保持的阶段。在此阶段，驾驶员对经过调整后确认的期望车速进行记忆保持，并以此期望车速为目标对所驾驶车辆的实际行车速度进行调控。在实际行驶过程中，当驾驶员感觉行车条件或交通环境发生变化而需要调整心目中的期望车速时，会按照图1中虚线的指向，重新确定新的期望车速。

通过以上期望车速形成过程的分析，不难看出，道路条件对期望车速的影响主要是横断面尺寸、道路线形和交通环境3个方面，其中横断面尺寸和车型是影响驾驶员期望车速选择的重要因素，线形和交通环境则是驾驶员调整期望车速的重要考虑因素。N.RASHEVSKY［3］最先提出公路最大安全运行速度预测模型，如公式(1)，国内不少学者将其引入到高速公路期望车速的预测中［4］。

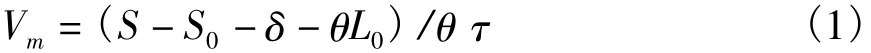
式中:Vm为期望车速，m/s;S为路基宽度，m;S0为车辆宽度，m;δ为车辆与行人间距，m;L0为车辆长度，m;θ为车辆侧偏角，rad;τ为驾驶员的反应时间，s。

该模型综合考虑了横断面尺寸和车型对期望车速的影响，得出的结果可认为是初始期望车速。高速公路由于线形指标较高且路侧封闭，对上述公式计算出的初始期望车速可以不作调整，直接用作驾驶员期望车速使用。但对于双车道公路，由于运行环境条件与高速公路明显不同，驾驶员在初定期望车速后还要根据路段内的交通环境和线形等情况，对初始期望车速进行调整并作记忆保持。

2 道路线形的影响及其修正

道路线形作为道路的重要组成部分会对驾驶员期望车速的选择产生重要影响。如果公路的某个线形单元为急弯陡坡或平纵面线形组合不良，驾驶员驾车至这些线形单元时，常常会因为紧张而引起心率急速加快;如果在整个路段范围内这样的线形单元较多，驾驶员在驾驶过程中必然会处于持续紧张状态，从而影响到驾驶员心目中的期望车速确定。

2.1 心率增长率分析

心率作为衡量驾驶员心理紧张程度的指标，能很好地反映车速、道路线形对驾驶员行车紧张性的影响。根据现有研究成果［5］，心率增长率为40%是心理高度紧张的阈值。因此，在分析线形与驾驶员期望车速的关系时，可以将40%的心率增长率作为判断驾驶员心理是否紧张的界限。根据《指南》［2］中运行速度计算对线形单元的划分要求，将路线划分为直线段、平曲线段、弯坡组合段和纵坡段4种线形单元;其中直线路段驾驶员的心率增长率较小，对驾驶员的期望车速选择不会产生影响。纵坡坡度对驾驶员心理的影响分为上坡和下坡两种情况，理论上在线形设计标准范围内，上坡不会给驾驶员的行车带来心理紧张。因此，对于影响驾驶员期望车速选择的弯坡组合以及纵坡路段，只需要考虑下坡的情况。平曲线段、弯坡组合段以及纵坡路段的驾驶员心率增长率模型如表1［6］。

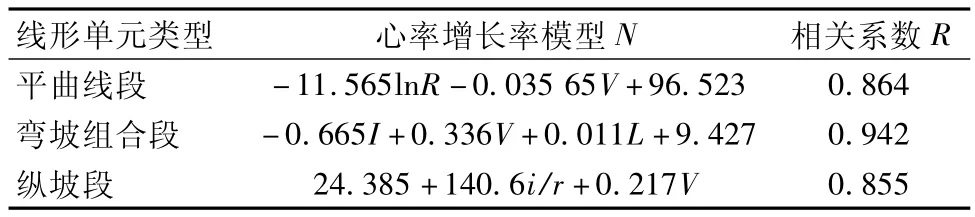
表1 心率增长率模型Tab.1 Model of heart rate growth

根据心率增长率模型以及调查路段中位运行速度，可以得出各种线形单元下驾驶员心率增长率达到40%的线形指标临界值，具体是:

1)平曲线段:半径小于120 m;

2)弯坡组合段:坡度与半径比值小于0.02;

3)纵坡段:各坡度情况下，坡长临界值见表2。

表2 纵坡路段临界坡长Tab.2 Limited slope length of slope sections

2.2 线形修正模型

根据以上驾驶员心率增长率模型，可以定性地确定在整个路段范围内哪些线形单元会对驾驶员的期望车速选择产生影响。为了量化线形对于期望车速的影响，笔者以这些线形单元占路段总长度的比例A作为衡量线形质量的指标。

式中:li为驾驶员心率增长率超过40%的线形单元长度;L为路段长度。

笔者实测了多条双车道公路长直线路段(包括山区长下破路段)最大稳定行驶速度，观测时段选择在交通量较小(不大于300 v/h)的自由流交通时段，在剔除了有横向干扰的路段后，对各观测路段期望车速差值T(初始期望车速与实测稳定速度的差值)和线形质量参数A进行回归分析，得到各车型线形修正模型如下。

2.2.1 小客车线形修正模型

T1= －0.000 8A3+0.453A2－0.141A+0.405，R2=0.936。

2.2.2 大货车线形修正模型

T2= －0.000 3A3+0.024A2－0.215A+0.853，R2=0.923。

3 交通环境的影响及其修正

我国双车道公路主要采用施划标线的方式分隔双向交通或主线交通与路肩上的交通干扰事件。这种分隔方式必然造成主线车辆受路肩交通的影响较大。横向干扰小的路段，驾驶员期望车速选择基本不受影响。横向干扰大的路段，则会对驾驶员期望车速选择和正常的驾驶行为构成干扰，从而使整个路段的车辆稳定运行速度降低。

横向干扰因素可分为6类，即拖拉机、支路车辆、路侧停车、行人、非机动车以及街道化程度等。为了量化横向干扰，这里将各类横向干扰因素分为5个等级，具体描述如表3。根据各影响因素的权重和级别，横向干扰级别(FRIC)可按下式计算:

FRIC=Int(0.25×TRA+0.2×EEV+0.18×PSV+0.15×PED+0.12×SMV+0.10×LU+0.5)

表3 各类横向干扰因素分级Tab.3 Classifications for various types of horizontal interference factors

为了量化横向干扰对主线车辆驾驶员期望车速选择的影响，选择平原区观测路段作为研究对象，横向干扰强度涵盖所有等级，此时线形对驾驶员期望车速选择的影响较小，驾驶员期望车速选择主要受横断面尺寸，车型以及横向干扰影响。图2为小客车初始期望车速与实测速度的差值(T3)分布散点图，大货车初始期望车速与实测速度的差值T4与T3基本相同。从图2中可以看出随横向干扰等级的增加而增大，两者之间有很强的线形相关性，当干扰等级为1时，期望车速基本不受横向干扰的影响;当横向干扰每增加一个等级，期望车速就会下降大约5 km/h。根据这一结论，同时借鉴现有的研究成果［7］，可以大致得到横向干扰等级与驾驶员期望车速调整量之间的关系，如表4。

表4 期望车速调整量Tab.4 The adjusted number of expectation speed

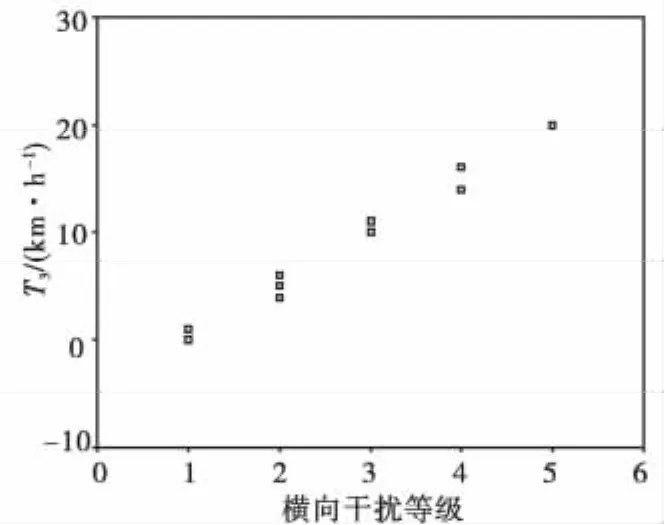
图2 T3分布散点图Fig.2 The scatteplot of T3distribution

4 期望车速确定方法及试验验证

综合上述分析，最终可以得到双车道公路期望车速预测模型如下，

小客车线形修正模型:

Vm修=(S －So－2δ－ θLo)/θτ－T1－T3

小客车线形修正模型:

Vm修=(S －So－2δ－ θLo)/θτ－T2－T4

在使用期望车速预测模型预测双车道公路期望车速时，主要有以下几个步骤:

1)根据设计速度、横断面尺寸以及横向干扰等级的不同将公路划分为多个分析路段并确定路面宽度等计算参数;

2)分析各路段内线形指标，计算线形质量参数A以及线形修正量;

3)根据横向干扰等级确定期望车速折减量;

4)根据预测模型预测各路段期望车速。

为了验证本文期望车速测算方法的合理性和可靠性，将未参与建模的某公路实测车速作为验证数据，该公路全长75 km，路基宽度12 m，平原微丘区路段设计速度80 km/h，山岭重丘区路段设计速度40 km/h，全线为沥青混凝土路面，且养护良好。公路分段及计算参数如表5，模型验证结果如图3、图4。

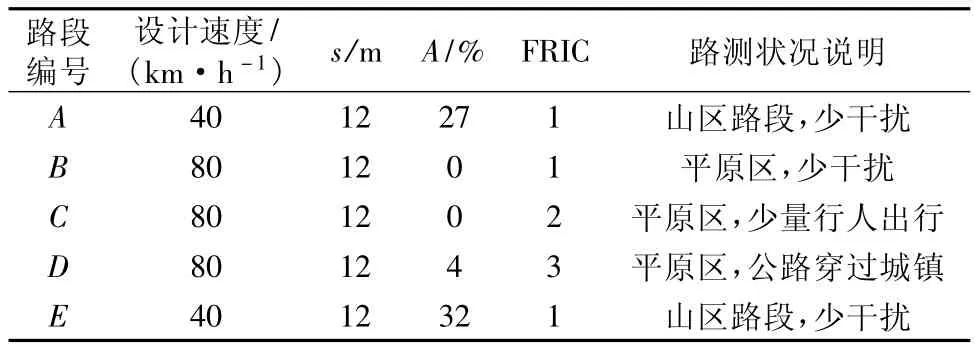
表5 公路分段及计算参数Tab.5 Road section and calculation parameters

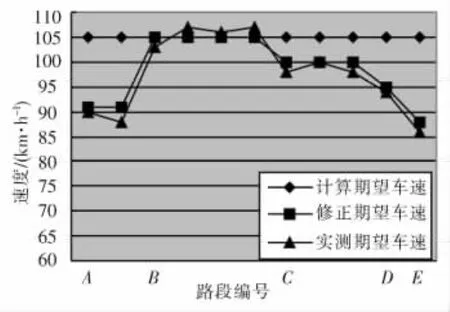
图3 小客车期望车速验证Fig.3 Validation of mini-buses’expectation speed

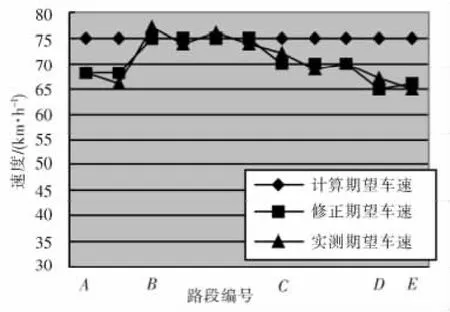
图4 大货车期望车速验证Fig.4 Validation of trucks’expectation speed

由图3、图4可知，本文预测方法得到的期望车速与实测期望车速较为吻合，最大相对误差仅6%，最大相对误差平均值为2.9%，其中路段B为横向干扰小的平原区路段，实测期望车速与式(1)计算的初始期望车速较为吻合，说明平原区横向干扰小的双车道公路，横断面尺寸以及车型是影响驾驶员期望车速选择的主要因素，驾驶员初步确定的期望车速可以作为路段最终的期望车速;其它路段由于存在横向干扰以及线形质量的差异(山区段)，经过驾驶员对初始期望车速的调整，最终确定的期望车速相对于B段有所降低;A段、B段、C段均布置了2个以上的测点，各测点实测期望车速基本保持一致，说明驾驶员对最终确定的期望车速实施记忆保持。通过以上分析充分说明了本文中期望车速预测方法的合理性与可靠性。

5 结语

双车道公路占我国干线公路总里程的95%以上，由于相对不够完善的道路行驶条件，干线公路上发生交通事故的概率和伤亡率都很高，基于运行速度的线形安全性检验，是提高双车道公路线形设计质量的有效办法;期望车速作为运行速度预测中的关键参数，对运行速度预测以及线形安全性检验产生重要影响。通过期望车速形成过程的分析，找出了影响驾驶员期望车速选择的道路因素，通过大量的实测数据分析，对现有的速度预测模型进行了改进，为利用运行速度检验双车道公路的线形安全性提供了良好的支持。

［1］郑安文.期望车速的意义及其影响因素分析［J］.武汉科技大学学报，2005，28(1):38 －41.

［2］JTG/TB 05—2004公路项目安全性评价指南［S］.

［3］Rashevsky N.Mathematical biophysics of automobile driving［J］.Bulletin of Mathematical Biophysics，1959，21:375－385.

［4］林雨，方守恩.灾害性天气环境下高等级公路车速管理［J］.自然灾害学报，2007，16(5):96 －99.

［5］王书灵.基于驾驶员心生理反应的山区双车道公路极限坡度坡长研究［D］.北京:北京工业大学，2005.

［6］乔建刚.基于驾驶员因素的山区双车道公路关键参数研究［D］.北京:北京工业大学，2006.

［7］王丽，罗满良，赵永国.公路环境对双车道公路运行速度的影响研究［J］.公路交通科技:应用技术版，2008(7):38－41.