泥石流运动力学研究现状及趋势
2010-08-16陈洪凯
刘 丽,陈洪凯
(1.重庆交通大学岩土工程研究所,重庆400074;2.重庆交通大学应用技术学院,重庆400074)
泥石流是一种全球性的自然灾害,是各种自然因素(地质、地貌、水文、气象、植被)和人为因素综合作用的结果[1-11]。泥石流因其形成过程复杂、爆发突然、来势凶猛、历时短暂、破坏力强而成为山区经济建设的一大灾害[3-5,10-11]。泥石流可在瞬间释放出大量的前期逐渐积累的物质和巨大能量[5-7,10],具有极大的破坏力,在泥石流所到之处,常常毁损公路、铁路、桥梁等交通设施及通讯基础设施[3-5],良田被冲毁,江河被堵塞,房屋被冲毁淤埋,严重危及人民生命和财产[4-7,10-11]。
我国山区和高原面积广阔,约占国土面积的66%,多处于季风气候区,加之断裂构造发育、地震频繁、地形陡峻,具备了泥石流形成条件,而表层岩体破碎,又由于人类活动影响,植被覆盖率越来越低,使我国成为世界上泥石流最多的国家之一。随着西部大开发的不断深入,人类活动范围的扩大以及各类建设工程的实施,加剧了公路泥石流发生频率,每年就公路泥石流造成经济损失近50亿元。
加深对泥石流暴发、运动及成灾机理等方面的认识,是控制治理泥石流灾害的首要前提,也是目前各国学者所关注的焦点之一。各国研究学者和工程技术人员,都从自身的学科领域和工作对象来研究和防治泥石流,概括起来有两个方面:①从地质地貌过程和现象方面为出发点的;②从气象水文过程来研究的。泥石流运动动力特征是泥石流学科的一个重要课题,因其具有突发性和灾害的严重性始终受到人们的重视,泥石流运动力学的研究主要集中在以下两个方面:泥石流运动过程中力学模型转化机理[5];泥石流流体的动力特性[12-14](流速、冲击力、磨蚀力)。
1 泥石流运动过程中力学模型
1970年美国地质地貌学家Johnson等[15]发表了第一篇有关泥石流运动模型的论文。由于泥石流运动速率与应力的关系呈非线性比例关系,不能应用牛顿流体模型。在非牛顿流体模型中,Johnson等选用宾汉黏性流模型(Bingham viscos fluid model),首次建立了泥石流运动方程,求解了泥石流最大流速。宾汉模型可解释观察到的一些泥石流现象,如泥石流“龙头”的巨砾聚集、大颗粒支撑结构和流体中存在的非变形“刚塞体”(rigid plug)现象,可以用宾汉模型得出较为合理的物理力学解释。英国 Keele大学的 Derbyshire教授等许多学者[15-20]认为,虽然认识到泥石流的运动和堆积与宾汉变形有关,但仍然有许多泥石流现象不能由宾汉模型得到圆满解释。
1978 年日本泥石流学家 Takahashi[15,18]教授的研究表明,许多泥石流的特性可以用膨胀流来模拟,并认为泥石流“龙头”的巨砾聚集是由于流体中颗粒的碰撞形成的。两年后这一观点基本成型,他借用英国科学家Bagnold[21]于1954年提出的分散应力的概念,1980年提出了泥石流拜格诺膨胀流模型(Bagnold dilatant fluidmodel),建立了泥石流运动方程,求解了泥石流平均速度和流体深度[18]。这一模型提供了泥石流启动和堆积的临界条件,解释了流体中有时不存在非变形“刚塞体”现象的成因机理和流体紊动对流体阻力的影响,并对泥石流大颗粒支撑结构和“逆向粒级”形成的物理力学机理给出了新的解释。
该理论认为,泥石流是一种胀流型流体,其剪切应力主要是由颗粒间的碰撞所产生。它提供了运动阻力和使砾石不沉积的支撑力机理,并且表明了泥石流不同于水流的运动速度分布以及水石流具有较大的阻力。这个理论的缺陷主要的是忽略了孔隙液体的动力学效应。它认为液相基质可以当作理想流体,其黏滞性可以忽略不计。这是不正确的,特别是当基质为黏土和粉沙悬浮液时更不正确。
1986年美国地质调查局 Cheng-lung Chen博士[19-20]基于宾汉流体方程,提出了一个通用的泥石流黏塑流模型(Generalized viscoplastic model)[22],并得出了这一模型的数值解。他认为,高度理论化的泥石流宾汉模型和拜格诺模型,尽管有它们的合理性和适用性,但由于过于复杂而在实际应用中失去了它们的可操作性。由他改进合并后的泥石流黏塑流模型,既包含了泥石流宾汉模型,又包含了泥石流拜格诺模型,泥石流宾汉模型和拜格诺模型都可以认为是泥石流黏塑流模型的亚模型。他认为这一改进的泥石流黏塑流模型为泥石流运动机理的进一步研究奠定了理论基础。
1993年美国O’Brien博士等对泥石流宾汉模型和拜格诺模型的结合做了新的尝试,试图建立起通用的泥石流运动模型,并称之为膨胀塑流模型(Dilatant P1astic model)[16,22-23]。这一模型是在美国工程兵部队于1986年创立的用于计算洪积扇上洪水和高含沙水流淹没范围的一维水力学模型的基础上,用二维连续流控制方程,采用有限元微分求解,建立的二维水流和泥石流运动模型,该模型可用于计算流速和流深。这一模型有一定的实用性,被法国学者Laigle和CoMssot认为是可以与Johnson模型和 Takahashi模型相提并论的成果[22-23]。这一模型主要适用于颗粒较细的“泥流”,而并不太合适于含有粗大颗粒的“泥石流”。
美国地质调查局 Iverson博士[24]于1997年发表了一篇重要泥石流论文:“泥石流物理学”。他比较了泥石流宾汉黏性流模型、泥石流拜格诺膨胀流模型和含有孔隙水压力的库伦颗粒流模型(Coulomb grain flow with variable Pore Pressure)。借用连续混合流理论 (Continuum mixturetheory)[24-26],根据能量守恒原理,Iverson提出了复杂的泥石流“混合流理论动量守恒方程”(Mixturetheory momentum conservation equations),用以分别计算泥石流体中的固体和液体的运动速度。
泥石流运动模型作为一种单相体模型是不完善的,泥石流本身是由固液气三相组成,有着复杂的结构组成和运动机理,近年来,随着流体力学、流变学和颗粒流学的进展,固液两相流理论[27-29]亦日趋完善,用两相流模型来概化泥石流运动体是较为合适的,而固液两相之间又是有着复杂的非线性关系相互影响。由上所述,泥石流体内液相与固相及固体颗粒间的相互作用十分复杂。把泥石流看作是两相流时,与一般固液两相流的类似之处在于需同时考虑固液两相物质的运动及其它们之间的相互作用。不同之处则在于“液相”和“固相”的含义已有所不同,为了反映泥石流与一般意义上两相流的这种差异,陈洪凯[30]建立的等效两相流模型为基础,把泥石流概化成两相组成,以黏度和粒径来概化划分固相和液相。运用两相流理论模型更能接近泥石流体的本质,通过野外考察和定位观测,结合理论分析和模型实验,更科学地分析泥石流运动机理和解释运动中的各种泥石流现象。
2 泥石流运动力学理论研究
2.1 泥石流流速
泥石流流速是泥石流动力学性质中最重要的参数,也是泥石流防治工程设计不可缺少的参数。因此,准确确定泥石流流速在泥石流计算中至观重要,同时也是泥石流工作极为关注的焦点。目前,国内外确定泥石流流速的方法很多,就其计算方法而言,概括起来可以分为两类[5]:一是黏性泥石流流速计算公式,二是稀性泥石流流速计算公式。
我国多从观测资料出发建立起一些地区性的经验公式,这些公式均以满宁公式为基础修正而成,具有鲜明的地区性。
陈洪凯[30]将泥石流体概化为由固相颗粒和浆体组成的等效两相流体,运用两相流理论构建了泥石流体分相流速计算公式:

式中:¯vs、¯vf分别表示泥石流体中固相和液相的实际流速,m/s;vs表示泥石流体中固相理论流速,m/s;α表示泥石流固相比;ρs、ρf分别表示固相和液相的平均密度,g/cm3;G表示固相流速差异系数,是泥石流固相比、流通区长度和泥石流厚度的函数;M为泥石流固液相流速比例,为固相比α的函数,计算公式为:
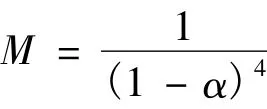
舒安平[31]通过对我国西部大量泥石流沟的实测资料进行统计分析,提出涉及参数较为全面、具有一定普遍意义的黏性泥石流运动速度公式的计算方法:
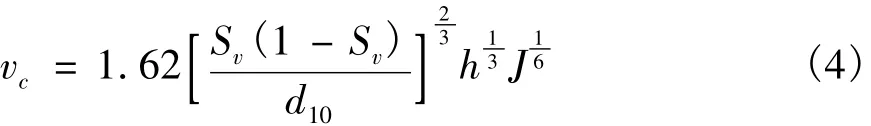
根据上述公式所计算出来的速度与实测速度比较都存在不同程度的误差,并且这些公式的适用范围只限于某一地区或某一类型的泥石流,地区性很强。因此,实际应用时,一般是将几个公式的计算结果与实测或调查资料进行比较后确定泥石流体的流速。
2.2 泥石流冲击力
泥石流在运动过程中对所触及的一切物体均会产生力的作用,泥石流动力学特征是泥石流在形成、运移、沉积等过程中所表现出来的一系列宏观特性,对泥石流动力学特征及其形成机制的研究是泥石流研究的一个重要内容,它不仅有利于我们认识泥石流这一特殊地质灾害,也是设计工程结构防治泥石流的基础和前提条件[12]。
泥石流冲击力的研究泥石流动力学的重要课题,它与被撞构件的尺寸和刚度有关,而且由于泥石流体中颗粒含量、颗粒尺寸及分布是随机无序的,因而其力源亦是随机无序的,这给泥石流冲击力的研究带来了许多困难,可运用数理统计和概率论的方法来解决。此外还需结合野外实测资料和室内试验分析其内在规律[32]。泥石流流体及所含的巨砾有极大的冲击力,往往是工程破坏的直接原因。20世纪70年代以来,我国与日本几乎同期进行这方面的野外测试工作。泥石流的冲击力包括两种:泥石流体的动压力和大块石的冲击力。文献[4]得出泥石流冲击压强计算式为:

式中:k为系数,根据云南东川实测资料取值为3~5;ρ为泥石流体平均密度,kg/m3。
吴积善等和周必凡等的泥石流动压力表达式为:

式中:P为被撞物单位面上所受的流体压力,kN;γc为泥石流体平均容重,kN/m3;vc为泥石流体平均速度,m/s。
根据蒋家沟1974—1975年冲击力测试资料,对上式进行了修正,修正公式为:

式中:k为泥石流不均匀系数,一般2.5~4.0。
对于泥石流体中巨砾对被撞结构物的冲击力,视所建立的计算模型的不同,建立的计算公式较多,主要有船筏撞击力计算公式、悬臂梁式计算公式、简支梁式冲击计算公式、撞击历时计算公式、落石冲击力计算式和弹性球冲击计算公式。
陈洪凯[29,32-33]把泥石流体概化为固、液两相流体,根据泥石流分相流速计算理论建立泥石流两相冲击力计算方法,并由泥石流冲击形迹计算泥石流冲击时间,可以有效地弱化现有冲击力计算的不确定性,并且可以在泥石流爆发后根据现场调查、取样分析来计算泥石流活动期间的冲击力及冲击时间长短。防治结构或岸坡表面单位面积承受的泥石流冲击力与泥石流液相浆体冲击力、固相颗粒冲击力等有关,即:

其显式表达式为:

式中:P的单位为Pa;K0为冲击力显式系数,一般取500~550,泥石流体黏度愈高取值愈大。
魏鸿[34]基于室内试验,建立了泥石流龙头对坝体的冲击力计算式:

式中:R为泥石流体中颗粒的代表粒径,m;K为常数;V0为泥石流中颗粒的运动速度,m/s;v0为泥石流内部压力波传播的速度(或称龙头冲击的初速度);ε为碰撞的能量恢复系数(可取0.6);ρ为龙头整体密度,kg/m3;ρL为液相密度,kg/m3(一般可取清水密度);λ为颗粒线浓度;ρs为颗粒密度,kg/m3;ρ0为龙头冲击坝前的密度,kg/m3。流体初始压力P0(kN)由式(13)计算:

式中:hm为龙头冲击前泥石流体的流深,m。
吴积善等[4]通过对蒋家沟泥石流观测将冲击力概化为锯齿形脉冲、矩形脉冲和尖峰形脉冲。如图1~图3。它们反映了泥石流冲击力随泥石流本身特征如流速、流量、容重、颗粒级配及颗粒形状等不同而变化。
刘雷激等[35]在中国科学院东川泥石流观测站于1982—1985年对蒋家沟泥石流冲击力进行了实地测量,采集了一批数据,将巨砾撞击力概化为矩形脉冲谱,而视泥石流浆体压力为三角形脉冲谱。
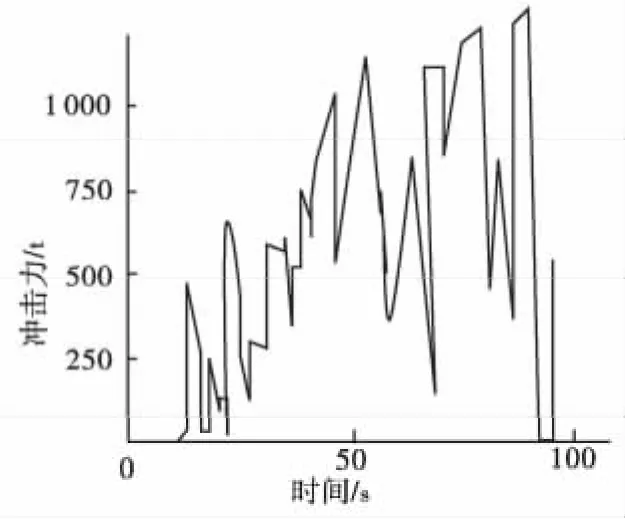
图1 锯齿形脉冲Fig.1 Pulse of hackle
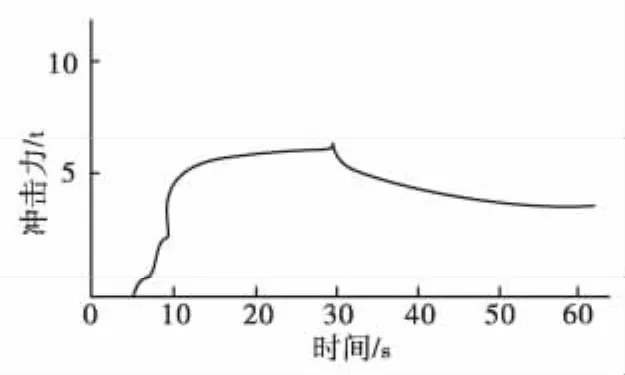
图2 矩形脉冲Fig.2 Pulse of rectangle
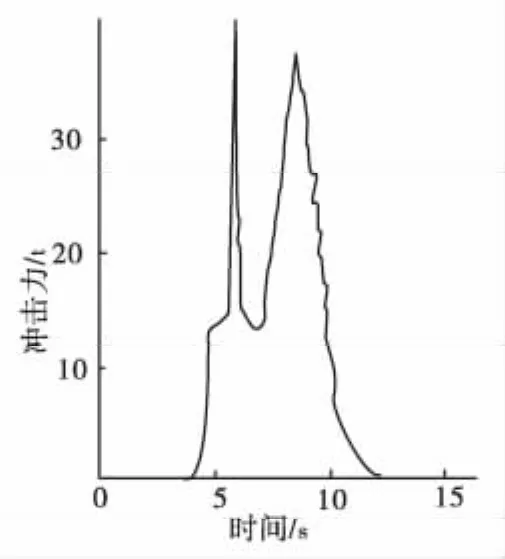
图3 尖峰形脉冲Fig.3 Pulse of aiguille
2.3 泥石流磨蚀力
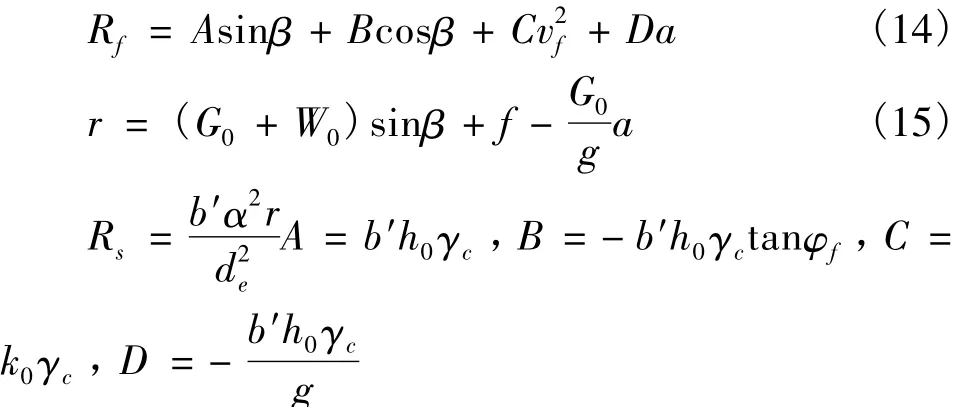
由于固、液两相泥石流体对防治结构的磨蚀作用包括浆体的磨蚀和固相颗粒的切削两方面,基于牛顿第二定律分别建立了泥石流液相浆体和固相颗粒的磨蚀力计算式[32]:式中:Rf为泥石流浆体对防治结构(如速流槽)的磨蚀力),kN/m;Rs为单位长度的速流槽壁面混凝土受到泥石流固相颗粒的切削力,kN/m;β为防治结构底板平均坡角,(°);G0为等效颗粒的重量,kN;W0为防治结构底板承受的上覆泥石流体重力,kN/m;a为泥石流运动加速度,m/s2;b′为防治结构内泥石流过流断面的宽度,m;h0为防治结构内泥石流体最大设计深度,m;γc为泥石流体平均容重,kN/m3;φf为泥石流浆体与混凝土壁面的动摩察角,(°)(取静摩擦角的0.4~0.5倍);k0为泥石流冲击动力实验系数(黏性泥石流取10~13,稀性泥石流取12~15);r为颗粒对速流槽壁面混凝土的摩阻力,kN/m;其余同前。
基于泥石流磨蚀力计算公式,运用量纲分析法建立了混凝土防治结构底板磨蚀速度及磨蚀量计算式。
3 泥石流动力学试验
试验研究是泥石流基本研究方法之一,泥石流试验包括现场试验、常规试验、流变试验和泥石流模型试验。在认识泥石流现象的过程中,对解决有关泥石流形成条件和运动条件的定性定量问题的研究起着很大的作用,是研究泥石流运动机理和泥石流动力学等的一个重要手段。通过试验研究泥石流体基本特征值、形成、运动及其动力问题,主要表现在以下几个方面[7]:
1)通过室内试验模拟泥石流,测量泥石流体的基本特征值和运动参数,如泥石流体的黏度、容重、流速等;
2)通过试验验证、校核和修正纯理论法所得到的解析关系式;
3)试验研究方法可用来拟定泥石流经验公式、理论试验公式。
在各类试样中,现场试验、常规试验和流变试验的研究较为成熟,伴随着各类试验仪器的开发应用,基本上建立了一套行之有效的观测方法、量测方法以及分析方法,加深了对泥石流的基本性质的认识理解。相对而言泥石流模型试验研究相似理论目前还处于探索阶段[36-37],周必凡等[13]将泥石流模型试验分为定性模型试验和定量模型试验。定性模型试验主要遵循模拟流体与原型流体的物理力学特征相同和试验设备的边界条件与试验流体的规模满足限制条件这两个方面,而定量模型试验除了以上两个条件外,还应保证模拟泥石流和原型泥石流的佛汝德数相等。
王兆印[14]采用多卵石进行水流冲刷沟床沉积物发展形成两相泥石流的试验,来研究泥石流形成和发展过程,以此建立龙头运动的能量理论和泥石流平均速度的理论公式,还分析龙头卵石的碰撞分选机理。魏鸿[34]进行了稳定均匀颗粒水石两相流龙头冲击坝体的水槽试验研究,分析了冲击荷载峰值的构成情况,运用压力波理论结合颗粒流的应力关系建立了龙头冲击力的计算办法,并对概化后的龙头计算其在冲击坝体时的作用力垂向分布。
王协康[36]从挟沙水流与泥石流模型相似律的关系入手,结合泥石流动力、动态、几何形态以及入流和边界条件对其相似律进行探讨,并与泥石流体本身的组成、结构和流变等特性联系起来,得到稀性泥石流的相似条件,并认为黏性泥石流应以高含沙泥浆为基础,进而提出了不同类别泥石流模型试验相似条件。
徐永年[38]利用可调坡水槽进行了松散崩塌土与水流掺混形成泥石流的实验,观测崩塌土运动距离及泥石流的形成过程,建立崩塌土流高比的计算公式,并在实验中发现一定形状的块状崩塌土与饱和度较高的下垫层之间存在超载孔隙水压力,超载孔隙水压力减轻了块体自重达到减阻的作用。
日本学者原田民司郎等人采用实测泥石流(水位、流速、输沙量)资料,将由雨量图算出的泥石流水位图作为上游的边界条件,应用泥石流输沙模型及其运动方程、连续方程式,再现了日本水无川1992年8月泥石流运动过程,并与实际沉积程度比较后加以检验以此研究泥石流运动规律,模拟泥石流运动过程,利于掌握其沉积、泛滥的危险区域,制定防灾减灾的对策[37]。
4 泥石流运动力学研究展望
4.1 泥石流运动力学基础理论研究的进一步深化
4.1.1 流速研究
泥石流流速是泥石流运动力学核心理论之一,现有公式都是侧重经验公式和地区性公式,而且流速的表示方法一般以断面平均流速或泥石流表面流速为主,泥石流近底流速的观测和计算公式表达较少。泥石流对沟谷及岸坡的冲刷以及河床断面的输沙起主导作用的是近底流速,故对近底流速的研究是必要的。通过试验测量近底流速的变化规律建立泥石流近底流速计算公式,分析近底流速与泥沙启动的关系。同时也可测定断面各点的泥石流流速及某个特征点的冲刷深度,利用流速与冲刷深度的对应关系,推求整个断面各对应流速测试点的冲刷深度,从而计算出断面冲刷量,为泥石流防治工程提供计算依据。
4.1.2 冲击力研究
泥石流冲击力研究主要集中在泥石流冲击频谱、冲击机理、岸坡动力演化以及冲击力计算等方面,属于泥石流动力学的核心理论之一,陈洪凯等(2006)[29]基于泥石流在沟岸或防治结构表面产生的冲击形迹运用两相流理论进行了泥石流冲击力研究。利用泥石流发生后的冲击形迹,反算泥石流的断面平均流速及冲击力,为防治工程提供较为精确的计算依据。同时对于泥石流冲击力的研究还可以通过建立流速的随机概率模型,利用频谱分析,将时域信号转化为频域信号,可以分析得出冲击力的随机概率模型。同时,利用冲击形迹理论来较核此冲击力随机概论模型,再通过试验分析不断的给予修正。
4.2 泥石流运动力学试验方法及试验仪器的不断研发和创新
现有泥石流专用仪器和传感器,如冲击力传感器和仪器,地声传感器,超声泥位计,大型砂浆流变仪,以微机为核心的数据采集和处理系统,记录表面流速和龙头形态的动态摄影和图象解析系统等等。但这些还远远不够,对泥石流脉动流速的测量及采集现有仪器无法测量及采集,没有脉动流速的实测资料,也无从知道流体内旋涡的尺寸,限制了运动方程解析的精度等等。所以就要求测量的试验仪器能够不断的研发。
4.3 加强基础数据信息的交流与合作
从事泥石流研究的各个研究单位各自积累了大量的基础数据,也各自做了很多的数据库,如陈洪凯[39]、唐红梅[40]在公路泥石流防治工程中作出了大量工作,但信息数据传播相对比较闭塞,很多基础试验在不停的反复测定,既费时又费力,很有必要建立行业性的规定,基本统一数据库的模式,建立情报交流制度。
[1]钱宁,万兆惠.泥沙运动力学[M].北京:科学出版社,1983.
[2]钱宁,张仁,周志德.河床演变学[M].北京:科学出版社,1987.
[3]钱宁,万兆惠.高含沙水流运动[M].北京:科学出版社,1989.
[4]吴积善,田连权,康志成,等.泥石流及其综合治理[M].北京:科学出版社,1993.
[5]陈洪凯,唐红梅,马永泰,等.公路泥石流研究及治理[M].北京:人民交通出版社,2004.
[6]吴积善,田连权,康志成,等.云南蒋家沟泥石流观察研究[M].北京:科学技术出版社,1990.
[7][前苏联]C.M.弗莱施曼.泥石流[M].姚德基,译.北京:科学出版社,1986.
[8]张宇,韦方强,贾松伟,等.砖砌体建筑在泥石流冲击力作用下动态响应实验[J].山地学报,2006,24(3):340 -345.
[9]唐邦兴,章书成.泥石流研究[J].中国科学院院刊,1992,2(10):124-128.
[10]康志成,李焯芬,马蔼乃,等.中国泥石流研究[M].北京:科学出版社,2004.
[11]王继康.泥石流防治工程技术[M].北京:中国铁道出版社,1996.
[12]陈洪凯.公路泥石流力学[M].北京:科学出版社,2007.
[13]周必凡,李德基,罗德富,等.泥石流防治指南[M].北京:科学出版社,1991.
[14]王兆印.泥石流龙头运动的试验研究及能量理论[J].水利学报,2001(3):18-26.
[15]姚德基,商向朝.七十年代的国外泥石流研究[C]//中国科学院成都地理研究所.泥石流论文集(1).重庆:科学出版社重庆分社,1981:132-141.
[16]Savage S B.Gravity flow of cohesionless granular materials in chutes and channels[J].Journal Fluid Mechanics,1979,92(1):53-96.
[17]Wang Y Y,Fei X J,Chen R.A modified rheological model of natural debris flows[J].Chinese Science Bulletin,1995,45(8):743-748.
[18]Takahashi T.Debris flow on prismatic open channel[J].Journal of the Hydraulics Division,1980,106(HY3):38l-396.
[19]Hampton M A.Buoyancy of debris flow[J].Journal of Sedimentary Petrology,1979,49(3):753-758.
[20]Wang G H,Sassa K,Fukuoka H.Downslope volume enlargement of a debris slide-debris flow in the 1999 Hiroshima,Japan,rainstorm[J].Engineering Geology,2003(69):303 -330.
[21]Bagnold R A.Experiments on gravity-free dispersion of large solid sphere in a Newtonian fluid under shear[J].Proceedings of the Royal Society,of London:A,1954(225):49 -63.
[22]Chen C L.General solution for visoplastic of debris flow [J].Journal of Hydraulic Engineering,1988,114(3):259-282.
[23]Gordon E G.Critical flow constrain flow hydraulics in mobilebed streams:a new hypothesis[J].Water Resources Research,1997,33(2):349-358.
[24]Iverson R M,Reid M E,LaHusen R G.Debris-flow mobilization from landslides[J].Earth Planet,1997(25):85 - 138.
[25]Iverson R M,Vallance J W.New views of granular mass flows[J].Geology,2001,29(2):115 -118.
[26]Iverson R M,Denlinger R P.Flow of variably fluidized granular masses across three - dimensional terrain[J].Journal of Geophysical Research,2001,06(B1):537-552.
[27]O’Brien J S,Julien P Y,Fullerton W T.Two-dimensional water flood and mudflow simulation[J].Journal of Hydraulic Engineering,1993,119(2):244-261.
[28]张远君,王惠玉,张振鹏,等.两相流体动力学[M].北京:北京航空学院出版社,1987.
[29]陈洪凯,唐红梅.泥石流两相冲击力及冲击时间计算方法研究[J].中国公路学报,2006,19(2):123 -129.
[30]Chen H K,Tang H M,Chen Y Y.Research on method to calculate velocities of solid phase and liquid phase in debris flow[J].Applied Mathematics and Mechanics,2006,27(3):42-48.
[31]舒安平,费详俊.粘性泥石流运动流速与流量计算[J].泥沙研究,2003(3):7-11.
[32]Chen H K,Tang H M,Wu S F.Research on abrasion of debris flow to high-speed drainage structure[J].Applied Mathematics and Mechanics,2004,25(11):1257-1264.
[33]陈洪凯,杜榕桓,唐红梅,等.泥石流泥石流龙头压胀机理探析[J].重庆交通大学学报:自然科学版,2008,27(5):790-793.
[34]魏鸿.泥石流龙头对坝体冲击力的试验研究[J].中国铁道科学,1996,17(3):50-62.
[35]刘雷激,魏华.泥石流冲击力研究[J].四川联合大学学报:工科版,1997,1(2):99 -102.
[36]王协康,方铎.泥石流模型试验相似律分析[J],四川大学学报:工程科学版,2000,32(3):9 -12.
[37]李维国,赵永光.日本应用实测洪水径流资料模拟泥石流运动过程[J].水土保持科技情报,2002(3):33-35.
[38]徐永年,匡尚富,黄永建,等.崩塌土流动化机理的实验研究[J].水利学报,2002,10(10):87 -90.
[39]陈洪凯,马康,马永泰,等.公路泥石流防治工程施工指南:Ⅰ[J].重庆交通学院学报,2006,25(4):26 -29,48.
[40]唐红梅,陈洪凯.公路特大型泥石流治理综合模式及应用[J].重庆交通学院学报,2005,24(6):112-116.
