剖析抛物线中的分类探究题
2010-08-14江西省安福县城关中学曹经富
✿江西省安福县城关中学 曹经富
在近几年各地中考中,有关探究相关图形的形状、位置,大小等试题频繁亮相于压轴题中,这类试题通常以抛物线为背景,以简单的几何图形为载体,借助点动、线动、图动的思想.进而分类探究相关图形的某种状态与结论.
分类讨论是初中常用的重要思想方法,无论是在生产活动、科学实验中,还是在日常的生活中,都常常需要用到它. 分类讨论是根据数学对象本质属性的相同点与不同点,将其分成几个不同种类的一种数学思想.它能训练人的思维条理性和严密性.实质上,分类讨论是“化整为零,各个击破,再积零为整”的数学策略.掌握分类思想,有助于我们提高理解知识,整理知识和独立获得知识的能力.而二次函数作为初中阶段最核心、最重要的内容,越来越被作为呈现知识、能力和思想的载体.为此,让我们结合有关试题,一同走进与抛物线有关的分类世界,感受它的魅力与奇妙动感.
一、有关等腰三角形的分类探究题
例 1:(2010年重庆市綦江县) 已知抛物线 y=ax2+bx+c(a>0)的图像经过点 B(12,0)和 C(0,-6),对称轴为 x=2.

(1)求该抛物线的解析式;
(2)点D在线段AB上且AD=AC,若动点P从A出发沿线段AB以每秒1个单位长度的速度匀速运动,同时另一动点Q以某一速度从C出发沿线段CB匀速运动,问是否存在某一时刻,使线段PQ被直线CD垂直平分?若存在,请求出此时的时间t(秒)和点Q的运动速度;若不存在,请说明理由;
(3)在(2)的结论下,直线x=1上是否存在点M使,△MPQ为等腰三角形?若存在,请求出所有点M的坐标,若不存在,请说明理由.
思路点拨:(1)可用待定系数法求解;(2)当条件既满足PD=QD,又满足PQ⊥CD时,是否存在PD的长.注意到当 PD=QD,PQ⊥CD 时,△PDC≌△QDC(HL),此时∠QDC=∠PDC,又∵∠PDC=∠ACD,于是可以判断DQ∥AC,∵D是AB中点,∴DQ是△ABC的中位线,DQ=1AC,AC 可求,那2么DQ亦可求,从而确定PD的长;(3)探究△MPQ为等腰三角形要分类讨论:若以PQ为等腰△MPQ的底边,则作PQ的中垂线,与x=1的交点即为点M;若以PQ为腰,则分别以P、Q两点为圆心,以PQ长为半径作圆,与x=1的交点即为点M,依此作法,可作出5个点.再利用勾股定理和一次函数的性质,解出点M的坐标.
解析:(1)∵ 抛物线过点 C(0,-6),∴c=-6,即 y=ax2+bx-6.

(2)存在,设直线CD垂直平分PQ,在Rt△AOC中,

∴点D在抛物线的对称轴上,连结DQ,显然∠PDC=∠QDC,
由已知∠PDC=∠ACD,∴∠QDC=∠ACD,∴DQ∥AC,DB=AB-AD=20-10=10,∴DQ为△ABC的中位线,
∴t=5÷1=5(秒).
∴存在t=5(秒)时,线段PQ被直线CD垂直平分,在Rt△BOC 中,,∴点Q的运动速度为每秒单位长度.
(3)存在.如下图,过点Q作QH⊥x轴于H,则QH=3,PH=9,在 Rt△PQH 中,
①当MP=MQ,即PQ为底边时,设直线CD的直线方程为 y=kx+b(k≠0),则,解得
∴y=3x-6,当x=1时,y=-3,∴M(11,-3).
②当PQ为等腰△MPQ的腰时,且P为顶点,设直线x=1上存在点 M(1,y),由勾股定理得:42+y2=90,即,∴
③当PQ为等腰△MPQ的腰时,且Q为顶点.过点Q作QE⊥y 轴于 E,交直线 x=1 于 F,则 F(1,-3),设直线 x=1 存在点 M(1,y)由勾股定理得(y+3)2+52=90:,即∴,综上所述,存在这样的5个点
点评:本题是集代数、几何核心内容于一体的综合题.在(2)它从一个新的角度提出问题,重在考查了学生化动为静及数形结合能力,在(3)中重点考查了探究等腰三角形存在情况的分类讨论.在探究等腰三角形的形状时,通常对已知线段为底和腰两种情况进行分析,考虑已知线段为腰时,又要分两种情况:线段两端点分别为等腰三角形的顶点.解题时要注意将有关点的坐标转化为相关线段的长,再借助等腰三角形的两边相等构建方程求解相关未知数或变量.
二、有关平行四边形的分类讨论题
例2:(2010年陕西省)如下图,在平面直角坐标系中,抛物线 A(-1,0),B(3,0)C(0,-1)3 个点.
(1)求该抛物线的表达式;
(2)点Q在y轴上,点P在抛物线上,要使Q、P、A、B为顶点的四边形是平行四边形求所有满足条件点P的坐标.
思路点拨:(1)已知3个点求抛物线的解析式可用一般式求解.(2)要使Q、P、A、B为顶点的四边形是平行四边形分两种情况考虑:①AB为边,则利用PQ∥AB且PQ=AB,从而可知P的横坐标是4或者-4,然后代人二次函数解析式,求出点P坐标;②如果AB为对角线,只要线段PQ与线段AB互相平分即可又知点Q在y轴上,且线段AB中点的横坐标为1,∴点P的横坐标为2,这时符合条件的P只有一个点记为P3,将x=2代入二次函数解析式即可求出.
解析:(1)设该抛物线的表达式为y=ax2+bx+c根据题意,得,解得
(2)①AB为边时,只要PQ∥AB且PQ=AB=4即可.又知点Q在y轴上,∴点P的横坐标为4或-4,这时符合条件的点P有两个,分别记为P1,P2.而当x=4时;当x=-4时,y=7,此时



②当AB为对角线时,只要线段PQ与线段AB互相平分即可,又知点Q在y轴上,且线段AB中点的横坐标为1,∴点P的横坐标为2,这时符合条件的P只有一个记为P3,而且当x=2时y=-1,此时P(32,-1).综上,满足条件的P为
点评:在探究4点构建的平行四边形中,其中只有两个点确定,其余两点为动点,则需要借助分类讨论的思想进行分析,即已知的两个点可能为所要探究平行四边形的边,也可能为对角线,再进一步借助平行四边形的边、角及对角线性质进行求解.
三、有关直角三角形的分类讨论题
例3:(2009年福建省宁德市)已知抛物线 C1:y=a(x+2)2-5的顶点为P,与x轴相交于A、B两点(点A在点B的左边),点B的横坐标是1.
(1)求P点坐标及a的值;
(2)如下页图(1),抛物线C2与抛物线C1关于x轴对称,将抛物线C2向右平移,平移后的抛物线记为C3,C3的顶点为M,当点P、M关于点B成中心对称时,求C3的解析式;
(3)如图(2),点Q是x轴正半轴上一点,将抛物线C1绕点Q旋转180°后得到抛物线C4.抛物线C4的顶点为N,与x轴相交于E、F两点(点E在点F的左边),当以点P、N、F为顶点的三角形是直角三角形时,求点Q的坐标.

思路点拨:将点B(1,0)代入C1的解析式能快速地求出a的值;在(2)中,当点P、M关于点B成中心对称时,要求出C3的解析式关键是求出顶点M点的坐标,而B点坐标为(1,0),利用对称性及通过添加适当的辅助线、全等知识等可得顶点M(4,5),且抛物线C3开口向下,运用顶点式便可求出C3的解析式;在(3)中,抛物线C1绕点Q旋转180°后得到抛物线C4.其实就是P,N关于点Q成中心对称,根据对称性可设字母m表示出N、E、F等各点的坐标,探究以点P、N、F为顶点的三角形是直角三角形时,要进行适当的分类考虑:3个角都有为直角的可能,再利用相关的勾股定理等确定其中所设字母m的值,进而求出Q点的坐标.
解析:(1)由抛物线 C1:y=a(x+2)2-5 得顶点 P(-2,-5).
∵ 点 B(1,0)在抛物线 C1上,∴0=a(1+2)2-5,解得
(2)连接PM,作PH⊥x轴于H,作 MG⊥x轴于G,∵点P、M关于点B成中心对称,∴PM过点B,且PB=MB,∴△PBH≌△MBG,∴MG=PH=5,BG=BH=3,∴ 顶点 M 的坐标为(4,5).
抛物线C2由C1关于x轴对称得到,抛物线C3由C2平移得到,∴抛物线C3的表达式为
(3)∵抛物线C4由C1绕点x轴上的点Q旋转180°得到,∴顶点N、P关于点Q成中心对称,由(2)得点N的纵坐标为5.
设点N坐标为(m,5),作PH⊥x轴于H,作NG⊥x轴于G,作PK⊥NG于K,∵ 旋转中心Q在 x轴上 ∴EF=AB=2BH=6,∴FG=3,点 F 坐标为(m+3,0),H 坐标为(2,0),K坐标为(m,-5),
根据勾股定理得 PN2=NK2+PK2=m2+4m+104,PF2=PH2+HF2=m2+10m+50,NF2=52+32=34.
①当∠PNF=90°时,PN2+NF2=PF2,解得,∴Q点坐标为
②当∠PFN=90°时,PF2+NF2=PN2,解得,


③∵PN>NK=10>NF,∴∠NPF≠90°.
点评:本题是一道集抛物线的变换及探究直角三角形存在性的综合题,解题关键是要弄清两个对称点之间横坐标、纵坐标之间的变量与不变量之间的关系.对于图像类的坐标问题,其基本的思想是“数形转换”,把根据已知条件、图形性质求出来的几何量,转化成点的坐标,或者是由坐标转化成几何量时都应注意对点的坐标符号或几何量的确定.在探究三个点是否构成直角三角形时,主要是运用勾股定理的逆定理进行验证,其中应进行分类讨论哪一条边可能为斜边.
四、有关三角形相似的分类讨论题
例4:(2010年甘肃省)如下图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与 y 轴交于点 C(0,-3),设抛物线的顶点为D.

(1)求该抛物线的解析式与顶点D的坐标;
(2)以B、C、D为顶点的三角形是直角三角形吗?为什么?(3)探究坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCD相似?若存在,请指出符合条件的点P的位置,并直接写出点P的坐标;若不存在,请说明理由.
思路点拨:(1)运用待定系数法可求解解析式;(2)结合B、C、D三点的坐标可计算出三边的长度,再结合勾股定理的逆定理可判断是否为直角三角形;(3)要探究以P、A、C为顶点的三角形与△BCD相似,其中△BCD已确定,则相似的对应关系存在多种可能,故需要采用分类讨论的思想进行考虑,即AC可能分别与△BCD的三边为对应边.
解析:(1)设该抛物线的解析式为y=ax2+bx+c,由抛物线与y轴交于点C(0,-3),可知c=-3即抛物线的解析式为y=ax2+bx-3.把 A(-1,0)、B(3,0)代入,得解得a=1,b=-2.∴抛物线的解析式为y=x2-2x-3.∴顶点D的坐标为(1,-4).
(2)以B、C、D为顶点的三角形是直角三角形.理由如下:过点D分别作轴、轴的垂线,垂足分别为E、F.在Rt△BOC中,OB=3,OC=3,∴BC2=18. 在 Rt△CDF 中,DF=1,CF=OF-OC=4-3=1,∴CD2=2. 在 Rt△BDE 中,DE=4,BE=OB-OE=3-1=2,∴BD2=20.∴BC2+CD2=BD2,故△BCD为直角三角形.

(3)连接AC,可知Rt△COA∽ Rt△BCD,得符合条件的点为O(0,0). 过A作AP1⊥AC交y轴正半轴于P1,可知Rt△CAP1∽Rt△COA∽Rt△BCD,求得符合条件的点为P(10,.过C作CP2⊥AC交x轴正半轴于P2,可知Rt△P2CA∽Rt△COA∽Rt△BCD,求得符合条件的点为P(29,0).∴ 符合条件的点有3个:O(0,0)
点评:本题以二次函数为载体,将勾股定理与相似相融合,解题的关键是能运用数形结合的思想将相关的点的坐标及时转化为相应的线段长,在探究相似时,应弄清哪些是已知的量(边),确定的量(边),进而运用几何图形(相似三角形)的性质分别对应列成比例式进行求解.
五、有关探究图形面积的分类讨论题
例5:(2010年山东省潍坊市)如下页上图所示,抛物线与 x 轴交于 A(-1,0)、B(3,0)两点,与 y 轴交于 C(0,-3).以AB为直径做⊙M,过抛物线上的一点P作⊙M的切线PD,切点为D,并与⊙M的切线AE相交于点E.连接DM并延长交⊙M于点N,连接AN.


(1)求抛物线所对应的函数的解析式及抛物线的顶点坐标;
(3)抛物线上是否存在点P,使得四边形EAMD的面积等于△DAN的面积?若存在,求出点P的坐标,若不存在,说明理由.
思路点拨:(2)连接MP,由条件可得半径为2,结合切线长定理可得△EAM≌△EDM,借助四边形EAMD的面积为,即△EAM的面积为,发现,这时要注意分类,点E可能在第二象限,也可能在第三象限,故点E的坐标有两个;结合△EAM三边的关系存在特殊角,进行借助特殊角的三角函数关系求解D点坐标(也存在两个,第一象限或第四象限),运用待定系数法从而得到两条直线BD的解析式(.3)要探究四边形EAMD的面积等于△DAN的面积,结合相关图形关系也就是S△EAM=S△AMD,即同底等高,可知切线PD与x轴平行,且到x轴的距离为2,应分类讨论:可能 y=2或y=-2,即将(x,2)和(x,-2)代入抛物线可得相应P点坐标.
解析:(1)因为抛物线与 x 轴交于点 A(-1,0)、B(3,0)两点,设抛物线的函数关系式为 y=a(x+1)(x-3),∵ 抛物线与 y轴交于 C(0,-3),∴-3= a(0+1)(0-3),解得 a=1,所以抛物线的解析式为 y=x2-2x-3=(x-1)2-4,因此抛物线的顶点坐标为(1,-4);
(2)连接 EM,∵EA、ED 是⊙M 的切线,∴EA=ED,EA⊥AM,ED⊥MD,∴△EAM≌△EDM,又四边形EAMD的面积为当点E在第二象限时,切点D在第一象限,在Rt△EAM中,∠DMB=60°,过切点D作DF⊥AB于F点,∴MF=1,DF=,则直线PD过的坐标代入,则函数PD的解析式为当点E在第三象限时,切点D在第四象限,同理可求直线PD的解析式为因此直线PD的函数关系式为y=-
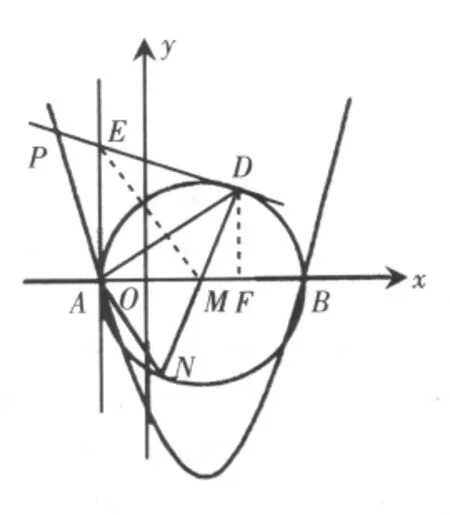
(3)若四边形EAMD的面积等于△DAN的面积,又∵S四边形EAMD=2S△EAM,S△DAN=2S△AMD,则 S△EAM=S△AMD,∴E、D两点到x轴的距离相等,∵PD与⊙M相切,∴点D与点E在x轴同侧,∴切线PD与x轴平行,此时切线PD的函数关系式为 y=2或 y=-2. 当 y=2 时,由 y= x2-2x-3 得当 y=-2时,由 y= x2-2x-3得.故满足条件点P的位置有4个,分别是
本题将一次函数、二次函数、直线与圆、三角函数等知识高度融合,在题型上虽较为传统,但却有力考查了学生综合运用知识融会贯通能力、分析问题、解决问题能力及分类讨论的能力.在近几年,有关抛物线与圆、面积的综合题不断被人所淡化,但它对于培养、训练与考查学生数学分析能力、逻辑推理能力、综合能力、数形结合、分类讨论思想及数学素养却是一道亮丽的风景和不可多得的好试题.
