风吸力下冷弯薄壁檩条稳定承载力分析和设计建议＊

宋晓光，张其林，刘沈如

（同济大学 土木工程学院，上海 200092）

由冷弯薄壁檩条、压型钢板及拉条组成的轻钢屋面，如图1所示，近年来广泛地应用于门式刚架、钢屋架等作为承重结构的屋面围护体系中.在风吸力作用下，檩条的下翼缘受压，由于屋面不能有效地阻止下翼缘受压时的侧向变形趋势，就会出现檩条在风吸力作用下的弯扭失稳.尤其在风压较大的地区，风吸力很可能成为檩条设计的控制因素.现行的《冷弯薄壁型钢结构技术规范》（GB50018－2002）[1]与《门式刚架轻型房屋钢结构技术规程》（CECS 102：2002）[2]均对檩条的稳定承载力计算有明确规定，但两者存在较大差异，计算结果也相差很大.而且对实际工程中广泛应用的嵌套搭接Z型连续檩条在风吸力作用下如何计算，国内各规范、规程均未做详细可行的规定.针对以上问题，本文将做详细分析并得出实用的设计公式.

图1 典型的屋面系统Fig.1 Typical roof systems

1 有限元分析模型

1.1 材料属性

钢材为Q235，屈服强度为fy＝235N／mm2，弹性模量为E＝2.06×105N／mm2，设材料的应力－应变关系为理想弹塑性模型，屈服准则采用等向强化Von－Mises屈服准则.

1.2 单元选取

为获得较好的计算精度，对简支檩条采用四节点Shell181单元.该单元适用于薄到中等厚度的壳结构，每个单元有四个节点，每个节点有六个自由度，而且该单元有强大的非线性功能.对套叠搭接的连续檩条采用八节点实体单元Solid45，该单元具有大变形和大应变能力.

1.3 边界约束

工程中典型的简支檩条的支座处构造如图2所示.为准确地模拟该构造，对有限元模型在简支支座处截面节点施加如下约束：对上下翼缘各节点施加约束uy，腹板各节点施加约束ux，翼缘与腹板相交节点施加约束ux和uy.另外为约束檩条刚体纵向位移，在檩条跨中截面腹板中间节点施加纵向约束uz.上翼缘中点（间隔250mm）通过自攻钉与屋面压型钢板连接，考虑到屋面板在其平面内剪切刚度较大，对上翼缘中线每间隔250mm的节点施加约束ux.根据文献[3]分析：当拉条截面能满足强度要求时，拉条的刚度对檩条承载力的影响可以忽略不计.因此能满足强度的拉条可视为腹板的平面外约束，对拉条处腹板截面节点施加约束ux.

图2 简支檩条支座处构造Fig.2 Support configuration of simply supported purlins

工程中典型的嵌套搭接连续檩条的支座处构造如图3所示.对有限元模型在连续支座处截面节点施加如下约束：对搭接檩条上下翼缘各节点施加约束uy，腹板各节点施加约束ux，翼缘与腹板相交节点施加约束ux和uy.另外为约束檩条刚体纵向位移，在檩条支座截面腹板中间节点施加纵向约束uz.对上翼缘中线每间隔250mm的节点施加约束ux；对拉条处腹板截面节点施加约束ux.对搭接檩条在螺栓处的节点采用耦合位移的方法来简化模拟螺栓的作用，未考虑搭接檩条间的相互接触作用.

图3 套叠搭接连续檩条支座处构造Fig.3 Support configuration of lapped continuous purlins

1.4 荷载作用

作用在屋面板上的风吸力通过均匀固定（一般间隔200～300mm）在檩条上翼缘中点的自攻钉传给檩条，因此可认为檩条在上翼缘中点连线上受到均匀分布的风吸力作用.为精确模拟檩条所受的横向均布线荷载，在有限元模型上翼缘所有中间节点上（间隔25mm）施加向上的节点力.

1.5 稳定承载力分析

本文使用ANSYS10.0进行稳定承载力分析，qcr为特征值屈曲分析所得到的理想弹性结构的理论屈曲强度，qu为极值点失稳型结构的稳定极限承载力.需要说明的是：作用在檩条上的线载荷qcr或qu是檩条承受风吸力与檩条承受屋面自重在沿风吸力风向分量的差值.本文中横向线荷载qcr和qu应视为风吸力与垂直于屋面的自重荷载分量的差值.

2 分析模型检验

2.1 简支檩条分析模型检验

2.1.1 理论解检验

两端简支的梁在横向均布荷载作用下的弹性临界弯矩理论解[4]：

以文献[2]附录E檩条计算例题中的简支檩条规格Z180×2.5为例，不考虑拉条及屋面板的影响，将式（1）理论解与采用特征值屈曲分析得到的数值进行对比：理论解Mcr＝3.35kN·m，qcr＝0.48kN／m；采用Shell181单元进行屈曲分析得到qcr＝0.50 kN／m，Mcr＝3.52kN·m.两者仅相差4.2%.采用Solid45单元进行屈曲分析得到qcr＝0.51kN／m，Mcr＝3.59kN·m.两者仅相差6.3%.因此对檩条采用特征值屈曲分析的精度是可靠的.

2.1.2 试验检验

与文献[5]中的实验数据对比验证稳定承载力分析所得极限承载力的精度.文献[5]中试验所用檩条为Z20024，截面尺寸为202mm×73（79）mm×21.5mm×2.4mm，屈服强度为fy＝450N／mm2，跨度l＝4 800mm，檩条跨中设一排撑杆，ly＝2 400 mm，檩距s＝2 500mm，屋面板为来实高强KL板，厚度0.65mm，惯性矩I1＝2×105mm4，试件破坏形式为弯扭整体失稳的脆性破坏，破坏位置在跨中附近，破坏时檩条的极限荷载为qu＝8.44kN／m.采用Shell181单元进行稳定承载力分析所得极限承载力为qu＝8.04kN／m，与试验结果对比，两者相差4.97%；采用Solid45单元进行稳定承载力分析所得极限承载力为qu＝8.46kN／m，与试验结果对比，两者仅相差0.24%，而且破坏位置均在跨中下翼缘与卷边翼缘相接处.因此对檩条采用稳定承载力分析所得极限承载力的精度是可靠的.

2.2 套叠搭接连续檩条分析模型检验

与文献[6]中的套叠搭接檩条试件的试验数据对比验证稳定承载力分析所得极限承载力的精度.文献[6]中试件ZA024R，截面尺寸为150mm×67.5（63.5）mm×16.5mm×1.7mm，屈服强度为fy＝450 N／mm2，弹性模量为E＝1.99×105N／mm2，试验测得跨中施加的最大集中荷载Pmax＝30.12kN，稳定承载力分析所得极限承载力为Pu＝28.16kN.与试验结果对比，两者相差6.96%，因此对套叠搭接檩条采用非线性屈曲分析所得极限承载力的精度是可靠的.

3 简支檩条在风吸力作用下的稳定承载力分析

本节对文献[2]附录B和C中所有规格的冷弯型钢檩条在各种常用跨度下做了稳定承载力分析，分析结果如表1和表2所示.其中：qu1为按文献[2]附录E公式所计算结果，为便于比较公式（E.0.1－1）右边设计强度f改用屈服强度fy；q′u1为本文后面所提出新设计公式（2）的计算结果；qua为 ANSYS10.0稳定承载力分析并考虑初始缺陷所得的横向均布荷载极值.跨度l＝4m时，檩条跨中不设拉条；跨度L＝6m时，檩条跨中设一道拉条；跨度L＝7.5m及L＝9m时，檩条跨中三分点处设两道拉条.拉条均设在檩条腹板靠近下翼缘的三分点处.

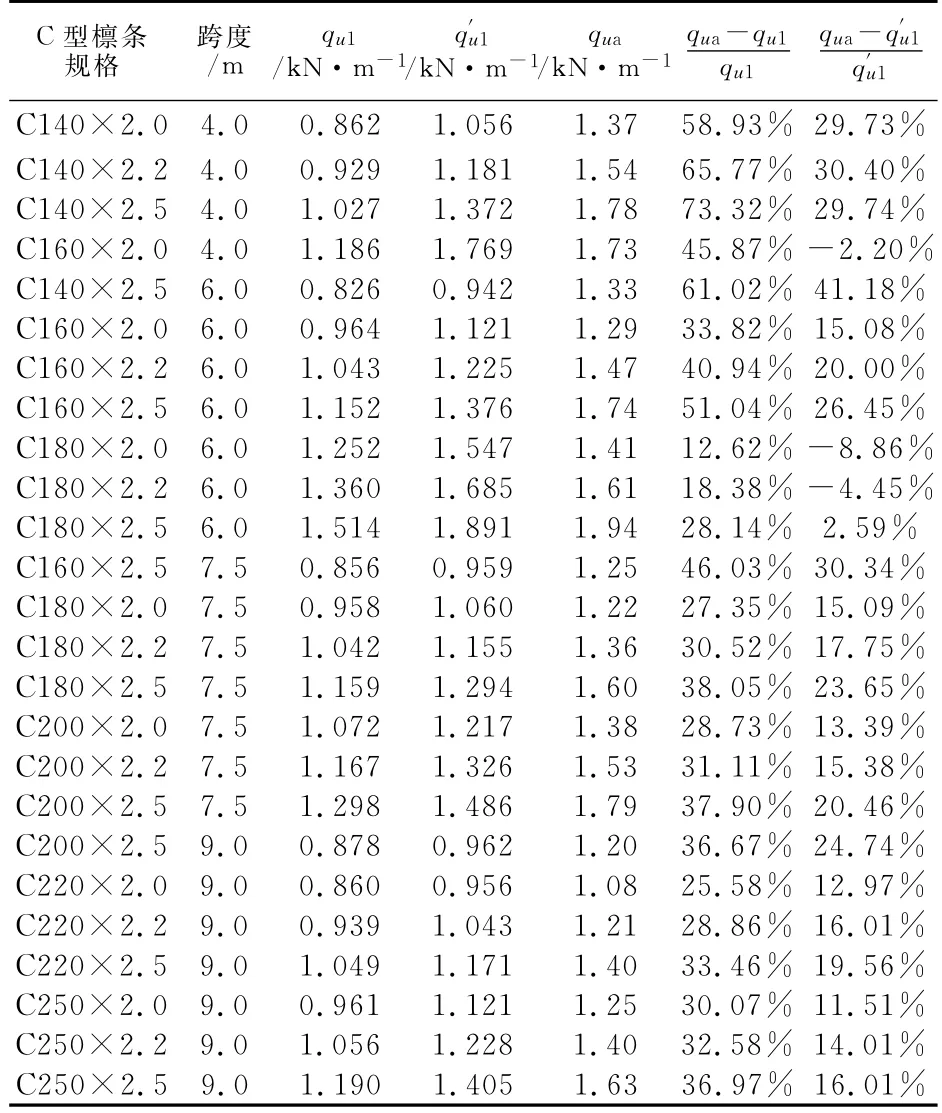
表1 C型檩条分析结果Tab.1 Results summary of c－shaped purlins

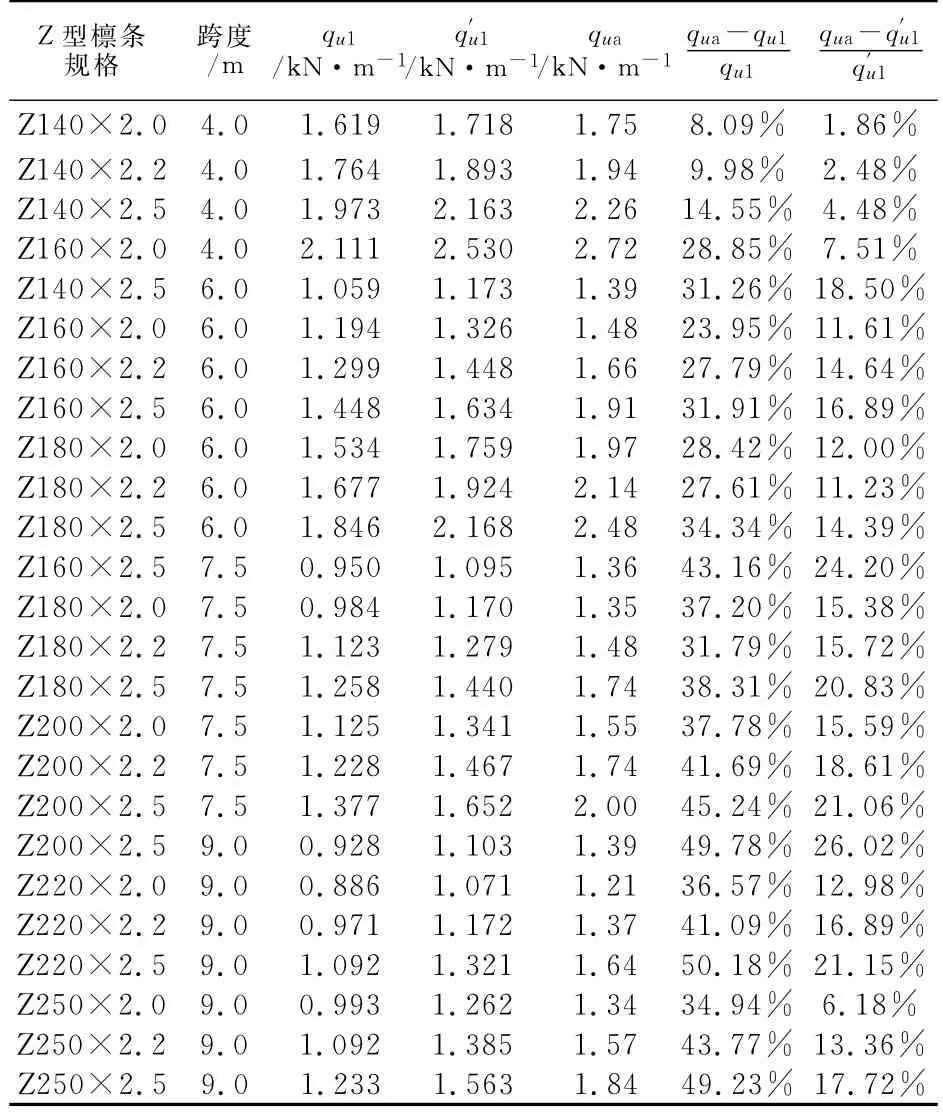
表2 Z型檩条分析结果Tab.2 Results summary of Z－shaped purlins

可以看出，文献[2]风吸力作用下的计算公式结果比较保守.与稳定承载力分析结果比较：C型檩条相差最大为73.32%，平均为38.15%；Z型檩条相差最大为50.18%，平均为33.90%.檩条稳定计算的关键在于如何模拟屋面板和拉条的侧向支承作用，现行轻钢规程在计算风吸力下檩条稳定计算时，着重考虑了屋面板对檩条的侧向弯扭约束刚度，但在计算稳定承载力降低系数χ时未考虑拉条的侧向支承作用，仅在计算下翼缘侧向弯矩M′y时，将拉条作为侧向支承点.而拉条（尤其是靠近下翼缘设置的拉条）与压型屋面板共同作用将形成对下翼缘较强的弯扭约束，从而在很大程度上提高了风吸力作用时下翼缘受压的稳定承载力.因而轻钢规程中风吸力作用下的计算公式结果是比较保守的.另外，轻钢规程中对能为檩条提供约束扭转刚度的压型屋面板有非常具体的要求：单波翼缘宽度不得大于120 mm；基板厚度不得小于0.66mm.这在实际工程中不一定能满足，因此在缺乏试验资料的情况下，采用规程提供的参数所计算出的结果必定与实际情况有偏差.

4 嵌套搭接连续檩条在风吸力作用下的稳定承载力分析

4.1 不同跨数单截面连续檩条稳定承载力分析

本节对文献[2]附录B中冷弯Z型檩条在单截面连续时，不同跨数下进行稳定承载力分析，以考察不同跨数对连续檩条稳定承载力的影响，分析结果如表3所示.qcr为ANSYS10.0特征值屈曲分析所得横向均布荷载值，qu为稳定承载力分析并考虑初始缺陷所得的横向均布荷载极值.跨度l＝6m时，檩条跨中设一道拉条；跨度l＝7.5m及l＝9m时，檩条跨中三分点处设两道拉条.拉条均设在檩条腹板靠近下翼缘的三分点处.

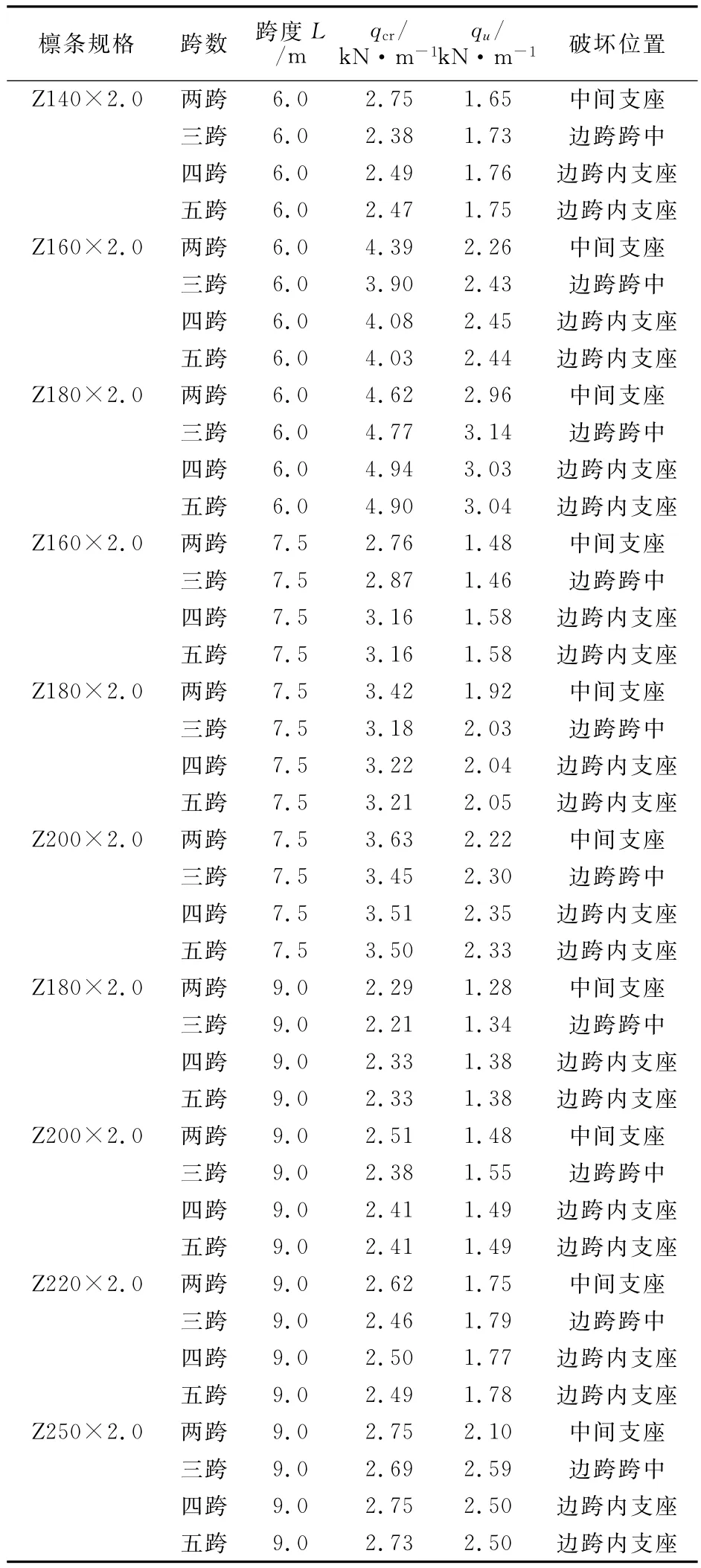
表3 不同跨数单截面连续檩条分析结果Tab.3 Results summary of single－section continuous purlins with varied span number

可以看出，随着跨数的增加，内力分布趋于均匀，横向均布荷载极值qu相应增大，这与连续梁在横向均布荷载作用下的弯矩分布图是相符的.屈曲破坏时的位置，除三跨檩条外，都是在边跨的内支座处，因此，支座套叠搭接对连续檩条的稳定承载力至关重要.三跨檩条由于边跨的跨中弯矩较大，与支座的弯矩比为0.8（而其余跨数檩条边跨跨中与支座的弯矩比为0.56～0.72），而且檩条在支座的约束要强于跨中，因此三跨檩条会在边跨跨中拉条处局部屈曲破坏.即使是横向均布荷载极值qu最低的两跨连续檩条，与相同规格、跨度的简支檩条相比，qu增大也达50%.因此下面针对两跨连续檩条支座处的套叠搭接进行分析.

4.2 套叠搭接两跨连续檩条的稳定承载力分析

套叠搭接两跨连续檩条承载力分析简图如图4所示.本节对文献[2]附录B中冷弯Z型檩条在套叠搭接两跨连续时进行稳定承载力分析，以考察不同搭接长度对连续檩条稳定承载力的影响，分析结果如表4所示.qcr为ANSYS10.0特征值屈曲分析所得横向均布荷载值，qu为稳定承载力分析并考虑初始缺陷所得的横向均布荷载值.拉条设置位置同前文所述.需要说明的是，分析时考虑搭接部分檩条上翼缘与屋面板采用自攻钉连接，将自攻钉处翼缘节点位移进行耦合来模拟该构造.

图4 套叠搭接两跨连续檩条分析简图Fig.4 Schematic diagram of lapped continuous purlins with double－spans

从分析可以看出，对于套叠搭接两跨连续檩条，破坏位置绝大多数出现于套叠搭接开始处截面，如图5所示，少数出现于跨中拉条处附近截面，没有出现于搭接段的破坏情况.而单截面两跨连续檩条破坏位置就在内支座截面处，这表明套叠搭接段增大了檩条的稳定承载力，使破坏截面外移至搭接开始处截面.通过静力计算可知，套叠搭接段的抗弯承载力可以达到单截面檩条的1.5～1.8倍.需要说明的是，对于套叠搭接多跨（五跨及以上）连续檩条，内力分布会更趋于均匀，破坏位置会更多出现于跨中拉条处附近截面.即使套叠搭接两跨连续檩条，当截面相对跨度较小且搭接长度较大，比如Z140×2.0，跨

表4 套叠搭接两跨连续檩条分析结果Tab.4 Results summary of lapped continuous purlins with double－spans

2表中h是檩条的截面高度.度6m，搭接长度LP＝15%L时，破坏位置就出现在跨中拉条附近的受压翼缘处.因此，套叠搭接开始处截面和跨中弯矩最大处截面都有可能是控制截面.

图5 支座处檩条破坏示意图Fig.5 Schematic diagram of support failure

从表4可以看出，随着搭接长度的增加，连续檩条的极限承载力相应提高.当搭接长度LP＝5%L时，已基本能达到单截面连续檩条的效果，但考虑到实际工程中为方便连接，檩条腹板上的螺栓孔一般为椭圆孔，受弯时会出现不同程度的嵌套松动[7－8]，可能会造成支座处承载力不足，因此建议在工程中宜取搭接长度LP＝10%L.

当搭接长度与檩条截面高度之比LP／h＝1.25～7.03时，搭接长度对檩条稳定极限承载力的影响不太显著.因此，搭接长度满足LP＝10%L后，再增加搭接长度对承载力没有显著提高，因为此时檩条跨中截面成为了控制截面.

5 设计建议

通过分析可以看出，由于在风吸力作用下屋面板与拉条能有效阻止檩条的侧移和扭转，Z型檩条的受力变形符合绕垂直于腹板的形心轴x1－x1轴弯曲变形的规律，如图6所示.因此，无论是Z型还是C型檩条，在风吸力作用下稳定承载力计算时可统一采用腹板平面内弯矩Mx1.以下公式中凡涉及Z型檩条的下标x均表示与形心轴x1－x1轴对应.

图6 Z型檩条示意图Fig.6 Schematic diagram of Z－shaped purlin

参照在腹板平面内受弯构件的稳定承载力计算公式，并考虑到在风吸力作用下屋面板能有效阻止檩条的侧移和扭转，可忽略My作用.即使考虑My作用，仍以文献[2]附录E例题为例，由My所产生的应力也只占到钢材设计强度f的0.75%，因此可忽略My作用.

考虑到利用冷弯薄壁型钢屈曲后强度，以有效截面模量Wex代替上式中截面模量Wx，为方便设计计算，可近似取有效截面模量Wex＝0.9Wx，则得到简化公式为：

其中檩条在腹板平面外屈曲的稳定系数φbx的计算同文献[1]附录A.2，如果公式所计算的φbx＞0.7，则应以φ′bx代替φbx，应按下式计算：

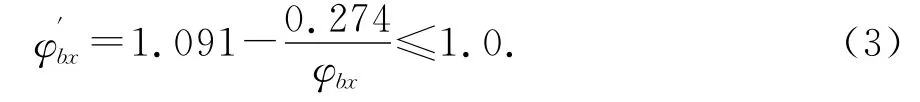
以上式中各符号的意义参见文献[1]附录A.2.

新设计公式（2）的计算结果与文献[2]中风吸力下檩条稳定承载力公式及有限元分析结果比较详见表1和表2.可以看出，新设计公式结果比较理想，有限元稳定承载力分析结果比较：C型檩条相差平均为17.22%；Z型檩条相差平均为14.45%.而文献[2]公式计算结果与有限元稳定承载力分析结果比较：C型檩条相差最大为73.32%，平均为38.15%；Z型檩条相差最大为50.18%，平均为33.90%.可见，公式（2）比文献[2]中风吸力下檩条稳定承载力公式应用更简便、更经济，可用于实际工程设计中.

对于简支檩条，控制截面就是跨中弯矩最大处截面.而对于套叠搭接连续檩条，由于搭接长度不同，支座搭接开始处截面和跨中弯矩最大处截面都有可能是控制截面.以五跨套叠搭接连续檩条为例，在风吸力q作用下，当搭接长度LP＝10%L时，支座套叠搭接开始处截面弯矩为0.077qL2，跨中弯矩0.078qL2，这时弯矩分布比较均匀，支座搭接开始处截面和跨中弯矩最大处截面几乎同时达到极限承载力，而支座搭接开始处截面约束一般强于跨中截面，因此破坏位置会更多出现于跨中，尤其是拉条处附近截面.

设计时可通过静力计算得到控制截面的弯矩，再利用公式（2）计算稳定承载力.

6 结 论

文献[2]中风吸力作用下的计算公式在计算稳定承载力降低系数χ时，未考虑拉条的侧向支承作用，结果比较保守.在文献[1]公式的基础上简化后，提出了新的檩条在风荷载作用下稳定性公式（2），应用更简便、更经济，可用于实际工程设计中.

采用Z型搭接连续檩条比简支檩条内力分布更均匀合理，极限承载力qu增大可达50%以上.

在套叠搭接连续檩条设计时，可通过静力计算得到控制截面的弯矩，再利用公式（2）计算连续檩条的稳定承载力.

搭接长度LP＝10%L时，能实现单截面连续檩条的效果.但搭接长度满足LP＝10%L后再增加搭接长度对檩条稳定承载力没有显著提高.

值得说明的是：本文分析的屋面板与檩条之间连接均为自攻钉连接，在这种连接构造情况下屋面板与拉条共同作用能有效阻止檩条的侧移和扭转.但对于目前设计、施工中屋面板与檩条之间采用其他形式的连接构造，如扣合式连接、立缝式连接等，屋面板与拉条共同作用能否有效阻止檩条的侧移和扭转，公式（2）是否仍适用，尚有待进一步研究分析.

[1] GB 50018—2002 冷弯薄壁型钢结构技术规范[S].北京：中国计划出版社，2002.GB 50018—2002 Technical code of cold－formed thin－wall steel structures[S].Beijing：China Planning Press，2002.（In Chinese）

[2] CECS 102：2002 门式刚架轻型房屋钢结构技术规程[S].北京：中国计划出版社，2002.CECS 102：2002Technical specification for steel structure of light－weight buildings with gabled frames[S].Beijing ：China Planning Press，2003.（In Chinese）

[3] 秦云，张耀春，王春刚.风吸力作用薄壁卷边C型檩条承载力分析和设计建议[J].建筑结构，2003，33（6）：6－8.QIN Yun，ZHANG Yao－chun，WANG Chun－gang.Load－carrying capacity analysis and design suggestions of C－shaped cold－formed purlins under wind uplift load[J].Building Structure，2003，33（6）：6－8.（In Chinese）

[4] 陈骥.钢结构稳定理论与设计[M].4版.北京：科学出版社，2008：325－327.CHEN Ji.Stability of steel structure theory and design[M].4th ed.Science Press，2008，Beijing：325－327.（In Chinese）

[5] 曾常阳.高强檩条在风吸力作用下稳定承载力的理论和试验研究[D].长沙：湖南大学，2002：45－75.ZENG Chang－yang.Theoretical and experimental investigations on stability bearing capacity of high－strength purlins under wind uplift loading[D].Changsha：Hunan University，2002：45－75.（In Chinese）

[6] HO H C，CHUNG K F.Experimental investigation into the structural behavior of lapped connection between cold－formed steel Z sections [J].Thin－Walled Structures，2004，42（7）：1013－1033.

[7] 童根树.钢结构设计方法[M].北京：中国建筑工业出版社，2007：285－294.TONG Gen－shu.Design method of steel structure[M].Beijing：China Architecture and Building Press，2007：285－294.（In Chinese）

[8] ZHANG Lei，TONG Gen－shu.Moment resistance and flexural rigidity of lapped connections in multi－span cold－formed Z purlin systems[J].Thin－Walled Structures，2008，46（5）：551－560.