卡氏积码的MDR码和自对偶码

刘修生

（黄石理工学院 数理学院，湖北 黄石 435003）

1 引言

在环Zk中的一个长度为n的码C是上的一个子集。如果这个码C还是上的子模，则称C是Zk上的线性码。特别地，如果码C是的自由子模，就说码C是自由的。文中所涉及的码均假设为线性码，对环绕空间附加标准内积。用来定义码C的正交码。为了方便读者，叙述已有的符号如下：

dH(C)表示码C的Hamming距离。

WH(C)表示码C的Hamming重量。

若C为线性码，则dH(C)=min{WH( c)∀c∈C}。

这里fi是正整数且满足。称为有限生成子模R的秩，记为rank(R)。注意这个有限生成子模R的元素个数为。

文献[1]证明了：若C是Zk上长度为n的码，则dH(C)≤n-rank(C)+1。

为此，引进了如下定义[2]。

定义1 如果Zk上长度为n的线性码C满足：

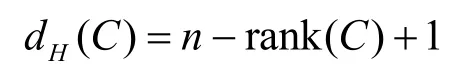
则称C是关于秩的一个极大距离码，简称C是MDR码。对于Zpk上的MDR码(p为素数)，文献[3]给出了一个对偶和一个矩阵刻划。对于一般的整数m，设它的标准分解式为本文的目的是：由上的码C1,…,Cs的特征来刻划Zm上码C。

2 中国剩余定理

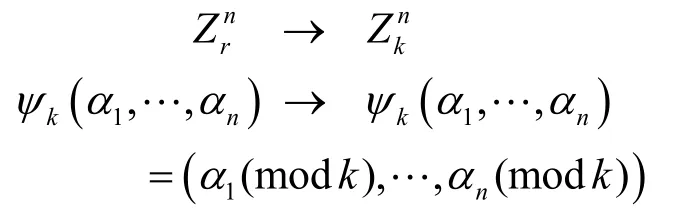
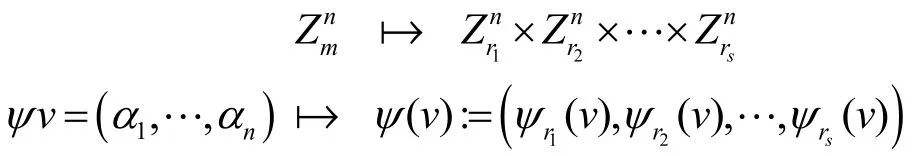
则由中国剩余定理知ψ是一个环同构[4]。

对于Zm中长度为n的码C，定义：

则易验证Ci是Zir的码，且ψ在C上的限制Cψ定义为：

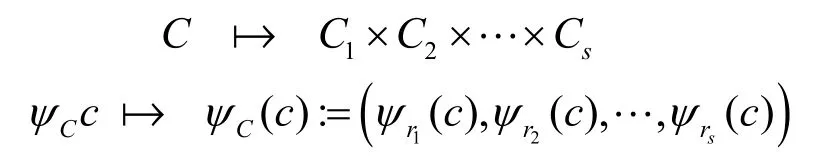
是码C与码C1×C2×…×Cs的一个同构，其中C1×C2×…×Cs称为码C1, C2,…,Cs的卡氏积码。

由上述可见，研究Zm上的码C可转化为研究码C1, C2,…,Cs的卡氏积码。

3 卡氏积码

设r1, r2,…,rs是两两互质的正整数，C1, C2,…,Cs分别是Zr1,…,Zrs上的码。由上定义，这s个码的卡氏积码为

引理1 记号如上，有：

证明 由子模同构定理知C1, C2,…,Cs分别同构于：

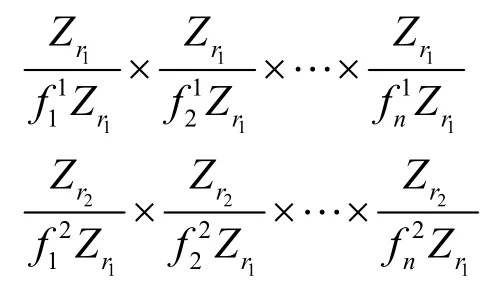
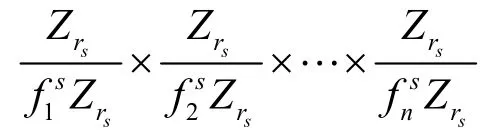
由整除的性质知，C1×C2×…×Cs也同构于：

从而，按秩的定义知，rank((C1×C2×…×Cs))=max{ rank(Ci)}。

引理2 记号如上，则

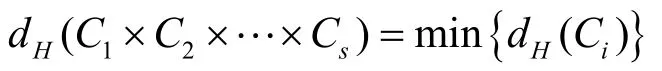
证明

定理1 设C1, C2,…,Cs分别是Zr1,…,Zrs上的码，如果对于每一个i，Ci是一个MDR码，则C=C1×C2×…×Cs是MDR码。

证明 由于C1, C2,…,Cs是MDR码，所以有：

从而：

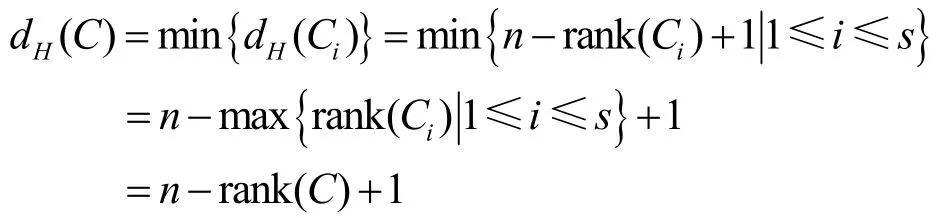
故C是MDR码。

定理1反之不然。

例如 设C是Z6上具有生成矩阵：

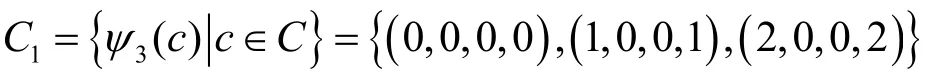
不是Z3上的MDR码。

定理2 设C=C1×C2×…×Cs，则

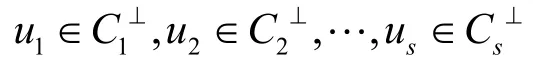
从而∀v1∈C1, v2∈C2,…,vs∈Cs,有：

于是对于任意v=(v1, v2,…,vs)∈C,有：

故uC⊥∈，因此

反过来，若ω=(ω1, ω2,…,ωs)∈C⊥,则对任意v=(v1, v2,…,vs)∈C,有：

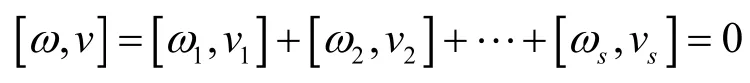
取v2=…=vs=0,v1为C1中任意元，则故ω1∈。

取v1=v3=…=vs=0,v2为C2中任意元，则[ω,v]=[ω2,v2]=0。

同理有ω2∈，如此类推，有ω3∈,…ωs∈。

推论1 C=C1×C2×…×Cs自对偶码的充要条件为C1, C2,…,Cs都是自对偶码。

证明 充分性显然。下面证明必要性。

对于每一个Ci，证明Ci=。

事实上，对任意的ci∈,有(0,…,0,ci,0,…,0)。由C=C1×C2×…×Cs为自对偶码知，(0,…,0,ci,0,…,0)∈C1×…×Ci×…×Cs。故ci∈Ci,从而，⊂Ci。

反过来，∀ci∈Ci,则：

故又有ci∈,从而Ci⊂。

综合得Ci=。因此C1, C2,…,Cs都是自对偶码。

[1] SHIROMOTO K. A singleton bound for codes over finite rings[J].Journal of Alagebraic Combinatorices,2000,(12): 95-98.

[2] DOUGHERTY S T, SHIROMOTO K. MDR codes over Zk[J]. IEEE Transactions on Information Theory, 2000,46(1): 265-269.

[3] SHIROMOTO K. Note on MDS codes over the integers modulo Pm[J].Hokkaido Math Journal, 2000, 29:119-148.

[4] DOUGHIERTY S T, HARADA M, SOLE P. Self-dual odes over rings and the Chinese remainder theorem[J]. Hokkaido Math Journal, 1999,28: 253-283.