非对称信道下协作通信系统中断概率的研究
2010-09-18啜钢刘圣温小军
啜钢,刘圣,温小军
(1.北京邮电大学 信息与通信工程学院,北京 100876;2.北京邮电大学 泛网无线通信教育部重点实验室,北京 100876)
1 引言
衰落信道下的中继传输已经被证明是减轻路径损耗和衰落影响的有效手段,近年来协作通信受到了广泛关注[1~3],其中,协作系统的中断概率性能和功率分配问题更是研究的热点之一[4~11]。文献[5]和文献[6]主要研究了协作系统只选择一个最优中继时的系统的中断概率性能。但文献[5]研究的是在对称信道下的中断概率性能和在此基础上的功率分配问题,而且其系统模型中没有考虑从源到目的节点的直通链路,本文则考虑了源到目的节点的直通链路;文献[6]虽然对非对称信道下的协作系统中断概率性能进行了一定研究,但其非对称模型仍然假设协作节点的源到中继节点的参数和中继到目的节点的参数是相等的,没有考虑中继节点位置的影响,即仍然存在对称性,本文中中继节点的位置则是完全随机的,因此对应的与信道有关的参数也是随机的,更加符合实际。文献[7~9]在对协作通信的研究中考虑了中继的位置因素,引入了路径损耗。但是文献[7]研究了只有一个源节点、一个中继节点和一个目的节点的系统模型,讨论了中继节点在源节点和目的节点之间的直线上变化时对系统误码率性能影响以及功率分配问题;文献[8]考虑了中继位置的随机性,推出了协作系统中断概率表达式,但其后面的分析中仍然把中继节点局限在源到目的的直线上来;文献[9]引入了非对称信道模型,但是没有研究其中断概率性能。与文献[7~9]相比,本文是在非对称信道下研究多个中继节点在一定区域内随机分布时系统的中断概率性能。文献[10]推出了对称信道下协作系统的中断概率表达式,其中断概率表达式中没有考虑中继位置,即在非对称信道下不适用。文献[11]提出了一种求多个独立指数随机变量和的方法,本文将其改进和扩展,应用到求解非对称信道下的中断概率中来。本文在文献[5~11]研究的基础上,考虑了源到目的节点直通链路,建立了适用于中继随机分布的非对称信道下协作系统数学模型,给出了协作系统中断概率表达式的闭式,并对协作节点的位置对中断概率和功率分配系数的影响进行了分析。
2 系统模型
该系统由一个源节点(单天线移动终端),一个目的节点(基站)和M个随机分布的潜在中继节点(单天线移动终端)组成,分别用 s、d及来表示。其模型如图1所示[9],图1中所有的节点都以半双工模式工作。其中,所有的潜在中继节点集合 Srelay构成了候选协作域,如图1中大长方形区域;能够帮助源节点进行通信的中继节点构成了协作域,如图1中小长方形区域。

图1 协作系统模型图
整个系统的协作协议采用解码中继[12](decode and forward)方式,整个协作通信过程分为2个阶段。
1) 第 1阶段:源节点s以 Ps的功率将自己要发送的信息进行广播,中继节点和目的节点对其进行监听,能够正确解调源节点所发信息的中继节点ri(i ∈ { 1,2,… ,M }),将成为协作节点,构成源节点的协作域,协作域用集合 D (N)来表示,表示协作域中用户的个数,表示对集合求势,在此阶段目的节点接收到信息但不解码。
2) 第2阶段:协作域中的各个中继节点以 Pri的功率将解调的信息重新编码后再发送一遍,目的节点此时将2个阶段的信息进行最大比合并(MRC)。
设定系统为总功率受限的系统,系统总功率为P,因此,协作中继节点的发射功率与源节点的发射功率满足:
当候选协作域中没有节点能够正确解调源节点的信息时,则源节点将以 P - Ps重新发送一次。这样可以保证无论是否有协作节点协作源节点进行通信,从目的节点看来发送端总以恒定的功率P进行发送。
假设源节点与目的节点、源节点与中继节点以及中继节点与目的节点之间的信道为平坦瑞利快衰落信道,即在相关时间内,从任意节点i到节点j的信道增益 hi,j保持不变,且假设它满足均值为0,方差为1的独立循环复高斯随机变量。如果只考虑小尺度衰落的话,信道就是对称信道。但在实际环境中影响信道的因素很多,包括大尺度衰落、小尺度衰落和阴影衰落等,在不考虑阴影衰落,只考虑小尺度和路径损耗的影响时,信道将变为非对称信道。目前多数文献在研究协作系统中断概率时,没有考虑到中继节点位置对中断概率及功率分配的影响,本文充分考虑到中继节点位置的影响,在非对称信道下研究协作系统的中断概率, 更接近实际情况。
3 中断概率分析
3.1 协作域的确定
定义中断概率outP 为任意2个节点之间的互信息I小于要求的频谱利用率R[1,2]的概率:

源节点的协作域是能够正确解码的中继节点的集合,因此,协作域 D (N )是所有中继节点集合Srelay的一个子集,定义为[5]

当中继节点i满足式(2)中的条件时,就认为它能够正确解码[2]。式(2)中 Ps表示源节点的发射功率; ds,ri表示从源节点到第i个中继节点的距离;dsβ,ri表示源节点到第i个中继节点的路径损耗;β是路径损耗因子,表示信号强度随距离衰减的速率,一般取2~6;表示源节点到第i个中继节点的信道功率增益,因为假设信道为瑞利衰落信道,所以服从指数分布。根据式(2),任意中继节点正确解调源广播信息即成为协作节点的概率为

中继节点之间能否正确解调源广播信息是相互独立的,因此,由候选协作域中M个节点构成任一协作域的概率为[6]

3.2 基于协作域的MISO的中断概率
协作域确定后,在某个相关时间间隔内,目的节点处采用MRC的信道容量可表示为
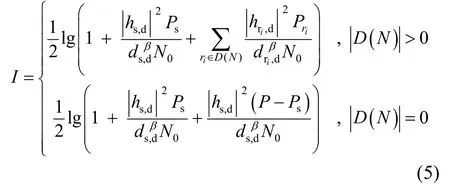
根据式(1)和式(5),协作域确定后系统的条件中断概率表示为


下面利用特征函数来求解这个条件中断概率:

文献[11]在推导过程中只把λ分为相等和不相等2类,而在本文模型下,因为中继可能成簇分布在不同的位置,即可能一簇中继(包含多个中继)在同一位置,而这样的中继簇又有多个,因此假设这些期望当中,有K1个取值为λe1,K2个取值为λe2,Km个取值为λem,其余L个取值各不相同,即λe1…互不相同且,则式(8)进一步变换并进行展开:

式(9)中的各个展开分式的系数Ak,Bk,…,El,都可以由留数法求得。对式(9)进行求逆变换可以得到γ的概率密度函数:

把式(10)代入式(7)中得到:

上式就是基于协作域的虚拟MISO系统的中断概率。
3.3 协作系统的平均中断概率
对于一个中继个数为N的协作系统,可能的协作域的个数(任意中继的可能组合)为2N个,考虑到所有情况,整个协作系统的平均中断概率就是所有中断情况发生的概率的和,表示为[6]

由上面假设知:Ps=αP,SNR = PN0,SNR ,对于式(4),令则式(4)变为

将式(11)和式(13)代入式(12)即得到协作系统的平均中断概率的表达式:

4 仿真和性能分析
仿真时,在平面直角坐标系中用坐标表示节点位置,对源节点和目的节点之间的距离进行归一化,即令s,d1d = ,源节点位于(0,0),目的节点位于(1,0),候选协作域中的节点随机地均匀分布于以源节点和目的节点的连线为轴线、边长为1的正方形内,即仿真分析区域是顶点坐标为(0,0.5),(1,0.5),(0,-0.5),(1,-0.5)的正方形。假设任意节点间的信道为瑞利衰落信道,信道系数为均值为 0,方差为1的循环平稳复高斯随机变量,路径损耗因子β随具体环境而有所不同,自由空间下一般取 2,城市蜂窝环境下取2.7~3.5[14],本文考虑城市蜂窝传播环境,这里取3β=。
图2是中继节点个数为5时,在不同功率分配系数α下的信噪比(SNR)和中断概率(outage probability)的关系曲线。图 2中不同的线型代表基于式(13)协作系统平均中断概率的理论值,离散的符号代表协作系统平均中断概率的 Monte Carlo仿真值。通过对比可以发现,理论值和Monte Carlo仿真值吻合地很好,证明了式(14)可以用来描述协作系统的中断概率性能。其中Theory表示理论曲线,Monte Carlo表示Monte Carlo仿真曲线。

图2 不同α下协作系统的中断概率的理论值和仿真值比较曲线
图3 是功率分配因子α=0.5时,不同中继节点个数情况下协作系统的平均中断概率与信噪比的关系曲线。每次随机生成多个不同数目不同位置的中继节点,采用Monte Carlo仿真得到系统平均中断概率,然后与理论值相比较,对比发现二者也是吻合的,说明了式(14)描述协作系统中断概率性能的精确性。

图3 不同中继节点个数下协作系统的中断概率的理论值和仿真值比较曲线
图4 是功率分配因子确定(α=0.5)时,相同个数的中继(中继个数为 10)不同位置分布时,协作系统的中断概率与信噪比的关系曲线。图中的“场景”即代表中继的不同的位置分布,从图4中可以看出,在功率分配因子和中继个数都确定的情况下,不同分布的协作域也会产生不同的中断概率性能,即中继节点的分布直接影响到系统的中断概率性能,因此,在研究中断概率时,其位置因素不容忽视。

图4 相同中继节点个数(10)不同位置分布下的中断概率曲线
图5 是不同中继个数下有直通链路和无直通链路下中断概率的对比。图5中实线代表有直通链路,虚线代表无直通链路,从对比可以看出,系统中有直通链路时的中断概率性能要优于无直通链路的情况,而当中继个数比较多时,这种差距就有变小的趋势。
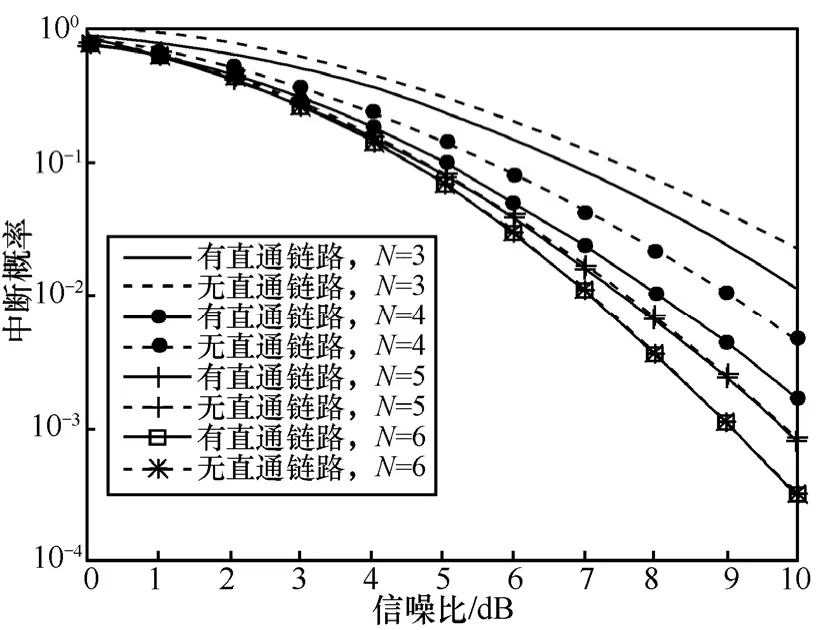
图5 不同中继个数下系统模型中有直通链路和无直通链路的对比
上面的仿真说明,式(14)可以比较精确地描述协作系统的中断概率性能,下面就在式(14)的基础上讨论基于中断概率性能的最优功率分配问题。
对于功率分配问题的研究,文献[6,9,15,16]已给出一些结论。其中文献[6]指出在采用 DF的协作方式下,前后2阶段的最优功率分配系数α为0.5;文献[15]通过统计搜索的办法指出在大多数网络配置情况下,最优功率分配系数α为0.5~0.6;文献[16]结合有限比特反馈进行功率分配使得中断概率得到较大改善。本文在非对称信道模型下对该问题进行分析。图6和图7为中继节点个数为8时,随机生成的协作域对最优功率分配系数α的影响。各图中曲线从上至下为信噪比从8~12dB变化时协作系统中断概率随功率分配因子α的变化情况。*代表最优α的位置,表1中(X ,Y)对应协作节点的坐标。
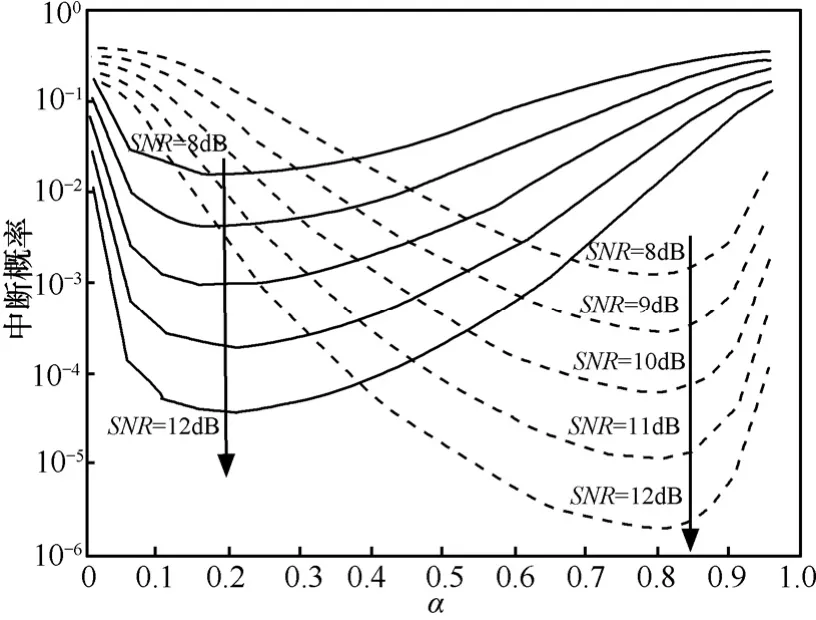
图6 α与中断概率的关系图(1)

图7 α与中断概率的关系图(2)
通过观察图6和图7可以发现,在非对称信道的协作通信系统中,考虑了源到目的节点的链路增益后,由于中继节点的位置的随机性,最优功率分配系数并不是一个固定的值,也不限于一个较小的范围,而是在一个较大的范围内波动。因此,对于一般的无线信道环境,考虑到中继节点的位置因素,在系统各节点无法得到精确的信道信息时,最优α的值随中继位置分布的不同而不同。
另外,从中断概率和α的关系图及其相对应的协作节点的位置坐标可以看出:当中继节点的平均位置分布在源节点和目的节点的中间时,最优α主要集中在0.5附近(如图7所示);而当中继节点的平均位置靠近源节点时,则最优α偏小(如图6中实线所示);中继节点的平均位置靠近目的节点时,最优α偏大(如图6中虚线所示)。这个结论与实际情况是相符的,当中继节点的平均位置靠近源节点时,源节点以较小的功率进行广播,就可以保证源到中继节点的链路不会中断,从而协作节点可以以更多的功率进行中继,整个系统的平均性能就能达到最优;而当中继节点的平均位置靠近目的节点时,源节点则需以较大的功率进行广播才能保证源到中继的链路不会中断,从而协作节点以比较小的功率进行中继,系统的平均性能就可以达到最优。
5 结束语
本文考虑了中继节点位置的随机性,首先建立了更贴近于实际的非对称信道下协作系统的数学模型,推导出了非对称信道下协作系统中断概率的表达式,仿真证明该数学模型可以比较精确的描述协作系统的中断概率性能。同时分析了节点位置对协作系统中断概率性能的影响,然后根据此数学模型研究了在总功率受限条件下协作系统的最优功率分配问题。研究表明功率分配因子α和路径损耗都会影响协作方案的中断概率。在考虑了位置因素的影响后,最优功率分配因子在一个较大的范围内波动,而且随中继的位置分布而变化。另外,从仿真结果可以看出当中继节点的平均位置靠近源节点时,最优的功率分配因子会小于0.5,即源节点以比较小的功率进行广播,整个系统的平均性能就能达到最优,而当中继节点的平均位置靠近目的节点时,源节点则需以比较大的功率进行广播,协作节点只要比较小的功率进行中继,系统的平均性能才能达到最优。

表1 协作节点位置坐标
[1] SENDONARIS A, ERKIP E, AAZHANG B. User cooperation diversity part i:system description[J]. IEEE Transaction on Communication,2003, 51(11)∶ 1927-1938.
[2] LANEMAN J N, TSE D N C, WORNELL G W. Cooperative diversity in wireless networks∶ efficient protocols and outage behavior[J]. IEEE Transactions on Information Theory, 2004,50(12)∶3062-3080.
[3] NOSRATINIA A, HUNTER T E, HEDAYAT A. Cooperative communications in wireless networks[J]. IEEE Communications Magazine ,2004, 42(10)∶74-80.
[4] HONG Y W, HUANG W J, CHIU F H, et al. Cooperative communications in resource-constrained wireless networks[J]. IEEE Signal Processing Magazine, 2007, 1∶ 47-57.
[5] BLETSAS A, SHIN H, WIN M Z. Cooperative diversity with opportunistic relaying[A]. IEEE WCNC[C]. Las Vegas, NV, USA, 2006.1034-1039.
[6] BLETSAS A, SHIN H, WIN M Z. Cooperative communications with outage-optimal opportunistic relaying[J]. IEEE Transactions on Wireless Communications, 2007, 6(9)∶ 1-11.
[7] KURNIAWAN E, MADHUKUMAR A S, CHIN F. Relaying and power control strategy for 2-hop distributed cooperative communication[A]. IEEE Vehicular Technology Conference 2008[C]. Singapore,2008. 98-102.
[8] PESCOSOLIDO L, BARBAROSSA S. On the optimal relay location and power allocation in a virtual array system with minimum overall outage probability[A]. Signal Processing Advances in Wireless Communications, SPAWC 2007[C]. 2007. 1-5.
[9] 高伟东, 王文博, 袁广翔等. 协作通信中的中继节点选取和功率分配联合优化[J]. 北京邮电大学学报, 2008, 31(2)∶ 68-71.GAO W D, WANG W B, YUAN G X, et al. Joint relay selection and power allocation optimization in cooperative communications[J].Journal of Beijing University of Posts and Telecommunications, 2008,31(2)∶ 68-71.
[10] 啜钢, 林立凡, 温小军等. 对称信道条件下协作通信系统的中断概率[J]. 北京邮电大学学报, 2009, 32(2)∶75-79.CHUAI G, LIN L F, WEN X J, et al. The average outage probability of cooperative communication system in symmetric wireless networks[J].Journal of Beijing University of Posts and Telecommunications, 2009,32(2)∶75-79.
[11] KHUONG H V, KONG H Y. General expression for pdf of a sum of independent exponential random variables[J]. IEEE Communications Letters, 2006,10(3)∶ 159-161.
[12] LANEMAN J N, WORNELL G W. Distributed space-time coded protocols for exploiting cooperative diversity in wireless networks[J].IEEE Transactions on Theory, 2003, 49(10)∶ 2415-2425.
[13] 王玉孝, 孙洪祥. 概率论与随机过程[M]. 北京∶ 北京邮电大学出版社, 2003.82-85.WANG Y X, SUN H X. Probability Theory and Stochastic Processes[M]. Beijing∶ Beijing University of Posts and Telecommunications Press, 2003.82-85.
[14] RAPPAPORT T S. Wireless Communications∶ Principles and Practice,Second Edition[M]. Beijing∶ Publishing House of Electronics Industry,2009. 138-139.
[15] LUO J H, BLUM R S, CIMINI L J, et al. Decode-and-forward cooperative diversity with power allocation in wireless networks[J]. IEEE Transactions on Wireless Communications, 2007, 6(3)∶ 793-799.
[16] 魏宁,张忠培,李少谦. 解码前传协同通信的断线率最小化[J]. 电子科技大学学报, 2009, 38(1)∶ 36-39.WEI N, ZHANG Z P , LI S Q. Outage minimization for decode and forward cooperative communication[J]. Journal of University of Electronic Science and Technology of China, 2009, 38(1)∶ 36-39.
