一种改进的D-S证据算法
2010-08-08张乐星
张乐星
(杭州师范大学 计算机系,浙江 杭州 310012)
多传感器信息融合技术是对来自不同传感器(信息源)的数据信息进行综合分析,以产生对被测对象统一的最佳估计,因而可以有效地解决单传感器信息的模糊点,增强系统正确决策的能力。由于传感器所提供的信息具有一定程度的不确定性,因此信息融合过程实质上是一个非确定性推理与决策的过程。
本文利用Dempster-shafer证据理论进行信息融合的算法,并针对D-S算法实现过程中存在的证据冲突问题提出了解决方法,对该理论的不足采用了修正的合成规则,最后通过仿真实验验证了该方法的有效性。
1 D-S证据理论基础[1-3]
D-S证据理论用“识别框架Θ”表示所感兴趣的命题集,定义了集函数 m:2Θ→[0,1],满足:

其中,m为识别框架Θ上的基本可信度分配;假如A属于识别框架Θ,则m(A)称为A的基本可信数,基本可信度反映了对A本身的信度大小。

即A的信度函数为A中每个子集的信度值之和。
关于命题A的信任,单用信度函数来描述还是不够的,因为Bel(A)不能反映出怀疑A的程度。所以,为了全面描述对A的信任,引入一个怀疑A的程度的量。
假如存在A属于识别框架Θ,定义:

Dou为 Bel的怀疑函数,pl为 Bel的似真度函数 Dou(A)为A的怀疑度,pl(A)为A的似真度。根据式(2),可以用与Bel对应的m来重新表示pl。
假如存在A属于识别框架Θ,则:
随着演出时间的增长,洛丽塔成了迈阿密海洋馆的“明星”,在人群中,有一个叫贝蒂斯的制片人,在支付了8000美元的好处费之后,海洋馆的老板答应配合他拍摄洛丽塔的纪录片。

[Bel(A),pl(A)]表示命题 A 的不确定区间;[0,Bel(A)]表示命题 A完全可信的区间;而[0,pl(A)]则表示命题“A为真”的不怀疑区间。
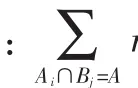
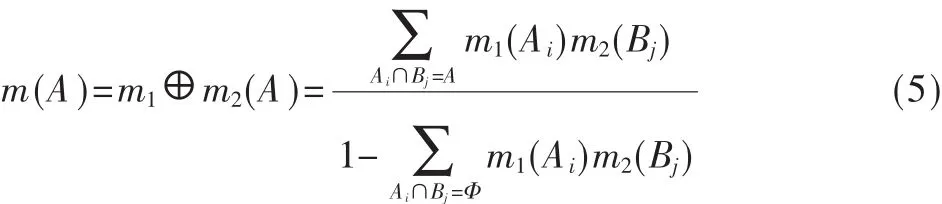
对于多个信度的合成(融合),令 m1-mn表示 n个信息的信度分配,如果它们是由独立的信息得出的,则融合后的信度函数可表示为:

2 D-S证据理论在应用中存在的证据冲突问题
D-S证据理论在应用中,当遇到证据相差较大(即证据冲突)时会出现很大的不足,主要表现在:
设 Θ={A,B,C}

则由D-S合成计算得出m(A)=m(C)=0,m(B)=1。说明 2个对B支持度极小的证据,合成后得到的结果竟然为B,显然是不合理的,即发生了证据冲突从而造成D-S算法的失效。
另外m的微小变化也会使组合结果产生急剧影响。对上述数据稍作修改:
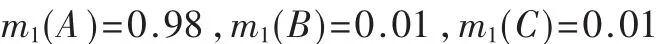
m2不变,则得 m(B)=0.01,与 m(B)=1相比,组合结果几乎是相反的。
最后,当一条证据与多条证据完全不一致时,会出现一票否决的结果。如设

如果有 m1=m3=m4=…=mn,则合成结果为 m(A)=m(C)=0,m(B)=1,显然是不合理的。
3 改进的冲突证据融合方法[4-5]
在实际应用中,若某个传感器工作异常则会出现证据冲突,此时就需要对该证据进行修正。设mi(i=1,2,…,m)为基本概率赋值函数;事件记为 Aj(j=1,2,…,n);用mij表示为第i条证据对第j个事件的基本概率赋值基元。
(1)证据的冲突判断
当一基元对某事件支持较大,而大部分支持该事件的基元都很小,则认为这一基元与其余基元产生冲突,表明其异常。但这种异常基元所支持的事件不应该是识别结论,即对识别结果不产生影响,所以此种证据冲突可不考虑。
但是当一基元对某事件支持较小,而其余支持这一事件的基元都很大的时候,也认为其异常,即发生了证据冲突,而由前文可知这种冲突会对识别结果产生影响,是本文所考虑的情况。采用加性策略,先找出支持最大的 h 个事件 Bk(k=1,2,…,h)。 令:

对 Sj进行排序,前 h个 Sj所对应的事件即为 Bk,然后在Bk中进行冲突验证。考虑基元在各自证据中所占比重对证据合成的影响,计算其对同一事件支持的基本份额:

计算pj与基元的差值:

给定阈值 α(α>1),若 1<Sij<α,则认为 mij为冲突证据,记为mik。若 Sij≥α或Sij<0则认为证据正常。其中阈值α的选取与BPA函数的数据准确度有关,BPA函数的数据准确度越高,支持同一事件的基元就越集中,α相应地就越大。

由此得到,判断证据mij为冲突证据的条件可表示为:

判断证据mij为正常证据的条件可表示为:

(2)对冲突证据mik进行修正

式中1/l为修正步长。l的选取与事件的个数n有关,从实际考虑,修正步长不能超过 1/n,一般取 l=2n。此时mik不满足证据的冲突判断条件,进行归一化处理得:

经过对冲突证据的检验及修正,便可继续使用D-S算法对证据进行合成。
4 实验结果
假设识别框架 Θ={A,B,C}, 对应的证据为 m1,m2,m3,直接利用证据理论进行融合,结果如表1所示。由表中计算结果可看出,最终的决策结果是B,显然与实际不吻合。
给定阈值α=2,经过对证据进行冲突检验及修正后再利用证据理论进行融合,结果如表2所示。此时识别结果是A,与直观相符。由仿真试验可以看出本文提供的算法可较好地解决证据理论在处理冲突证据时的不足。
本文提出了一种改进的D-S证据算法,该方法通过对证据冲突检验、修正,很好地解决了D-S证据理论对冲突证据进行融合时的不足,保证了非冲突证据的有效合成,提高了识别结果的正确性。
[1]BOGLER R L.Shafer dempster reasoning with application to muotisensor target identification system[J].IEEE Trans.On Syst Man and Cybern, 1981,17(6):415-418.
[2]段新生.证据理论与决策、人工智能[M].北京:中国人民大学出版社,1993.
[3]陈寅,林良明,颜国正.证据理论应用于多传感器融合不确定性分析[J].测控技术,2000,19(7):27-28.
[4]张淑清,邓红,王艳玲.D-S证据理论在数据融合中的应用及改进[J].传感技术学报,2003(1):80-81.
[5]张乐星,罗志增,叶明.用证据理论实现机器人多感觉信 息 的 融 合[J].机 电 工 程 ,1999(5):79-80.
