基于灰色DGM(2,1)模型的四川省铁路货运量预测

吴 丹

（西南交通大学 交通运输学院，四川 成都 610031）

铁路货运量是铁路运输能力的一个重要指标，对四川省铁路货运量进行预测，对相关管理部门具有重要意义，通过对四川省历年铁路货运量数据分析得出其变化过程为非单调的摆动发展序列，因此本文通过探讨DGM(2,1)模型来对四川省铁路货运量进行预测。

1 灰色预测DGM(2,1)模型简介

GM(1,1)模型适用于具有较强指数规律的序列，

只能描述单调的变化过程，而对于非单调的摆动发展序列或有饱和的S形序列，则可通过DGM(2,1)模型的建立来进行研究。

1.1 灰色预测DGM(2,1)模型的建立[1]

对于设有n个原始数据样本非负序列X(0)=(x(0)(1),x(0)(2),…,x(0)(n))，其1-AGO序列x(1)为：x(1)= (x(1)(1),x(1)(2),…,x(1)(n))，其中x(1)=k=1,2,…,n；1-IAGO序列为：α(1)X(0)=(α(1)x(0)(2),α(1)x(0)(3),…,α(1)x(0)(n))，其中，α(1)x(0)(k)=x(0)(k)-x(0)(k-1)，k=2,3,…,n；称=b为DGM(2,1)模型的白化方程。式中a,b为参数，根据最小二乘法其估计值为：

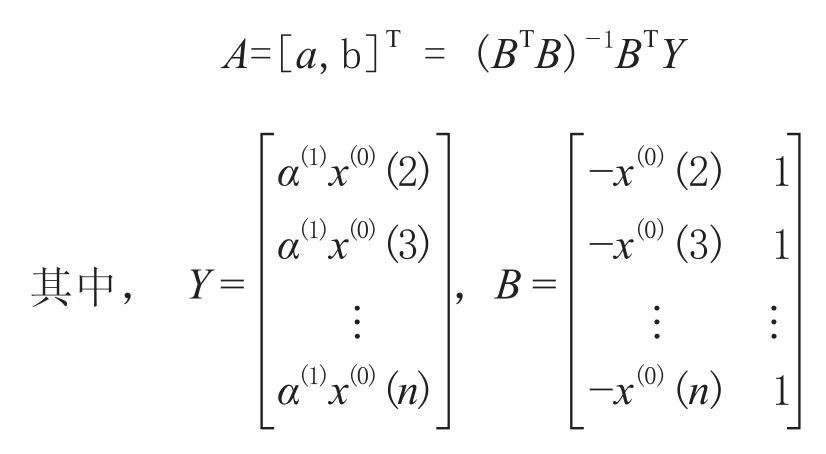
解微分方程可得DGM(2,1)模型的时间响应序列如下：

对于上式中计算出来的一阶累积序列进行还原，得各时段的预测值为：

1.2 模型精度检验

设原始数列为X(0)= (x(0)(1),x(0)(2),…,x(0)(n))，相应的灰色模型预测序列为

（3）计算灰色绝对关联度：

（4）计算小误差概率：

按上述几项指标，其精度指标见表1。

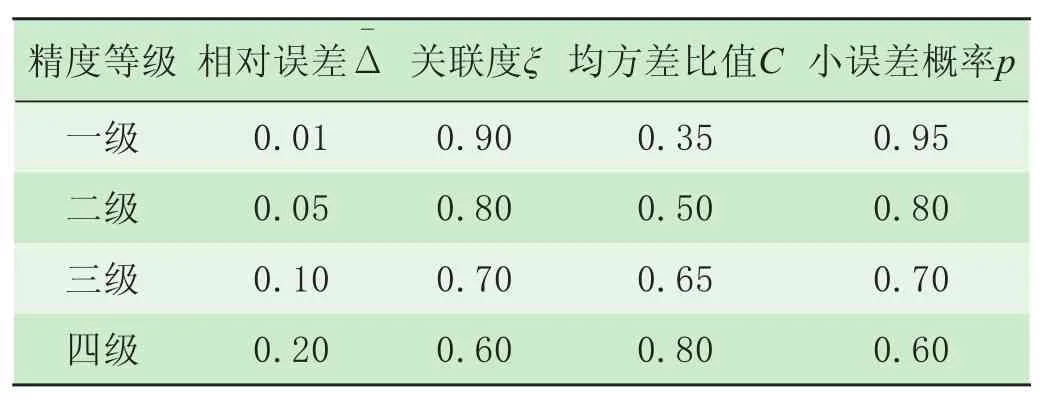
表1 精度检验等级参照表

2 灰色预测DGM(2,1)模型在铁路货运量预测中的应用

2.1 模型的建立

2002—2008年四川省铁路货运量的数据[2]，见表2。由表可知2002—2008年的货运量并不是呈现一个单调的变化发展趋势，2004—2006年呈现了一个与整体变化趋势相反的下降趋势，下面通过建立灰色DGM(2,1)模型来分析出四川省铁路货运量的未来发展趋势。

表2 2002—2008年四川省铁路货运统计数据

（1）设x(0)为2002—2008年四川省铁路货运量的原始数据序列，即X(0)=(x(0)(1), x(0)(2),…, x(0)(7))=（6 547，6 937，7 634，7 335，7 289，7 597，7 681），引入二阶弱化算子D2，令X(0)D=(x(0)(1)d, x(0)(2)d,x(0)(3)d,…, x(0)(7)d )，其中x(0)(k)d=(x(0)(k)+x(0)(k+1)+…+x(0)(7))，k=1,2,…,7，以及 X(0)D(2)=(x(0)(1)d2,x(0)(2)d2,x(0)(3)d2,…, x(0)(7)d2) ，其中x(0)(k)d2=(x(0)(k)d+x(0)(k+1)d+…+x(0)(7)d)，k=1,2,…,7。X=ΔX(0)D2=（7 503.68，7 539.53，7 565.01，7 579.45，7 614.11，7 660.00，7 681.00），则X的1-AGO序列为X(1)= (x(1)(1),x(1)(2),x(1)(3),…,x(1)(7))= (7 503.68，15 043.21，22 608.22，30 187.68，37 801.79，45 461.79，53 142.79)，其1-IAGO序列为α(1)X=(α(1)x(2),α(1)x(3),…,α(1)x(7))=(35.851,25.477,14.448,34.653,45.889,21.000)；根据最小二乘法可得

2.2 精度检验

由各指标计算公式得出了2002—2008年铁路货运量预测值的各精度指标值，见表3。

表3 DGM(2,1)模型精度检验值

3 预测结果

通过对四川省铁路货运量数据进行分析，引入灰色DGM(2,1)预测模型，其预测结果见表4，由表得出四川省未来几年的铁路货运量呈现单调的递增趋势，有着良好的发展态势。

表4 铁路货运量灰色预测结果

[1] 刘思峰，党耀国. 灰色系统理论及其应用[M]. 北京：科学出版社，2005.

[2] 四川省统计局. 四川统计年鉴2009[M]. 北京：中国统计出版社，2009.