进入角约束下的攻击机空间远距引导研究
2010-08-05蔡满意李雪松
陈 冰,蔡满意, 朱 凡,李雪松
(空军工程大学工程学院,西安 710038)
0 引言
攻击机远距引导是指战机根据空中/地面指挥系统所给的目标信息,飞向指定战斗区域,通常与目标的距离小于机载雷达探测距离[1],并具有一定的战术优势。为了具有较好的隐蔽性,此阶段机载雷达一直处于关闭状态。
随着战机和机载武器的发展,攻击机的精确打击和对运动目标拦截的能力要求越来越高,这对指挥引导的方法要求也越来越严格。一些文献[2]在研究引导时,只是将导引问题限制在一个水平面或垂直平面内,这是出于简化问题的考虑,便于方便研究引导律的特性,但实际的引导问题是在复杂的三维空间中。文献[3-6]指出导弹导引的目的是直接击中目标,要求脱靶量越小越好,要求精度要高。而战机远距引导只需要求把战机引导至有效的攻击空域,更多的是强调进入指定空域时的战术优势。本文主要针对的是实际战机引导问题,须将导引问题放在三维空间中加以研究。
1 空间运动模型的建立
由于指定空域位置一般不变,引导战机至指定空域,可以建立如图1所示的坐标系。计算时涉及的坐标系如下所示。
1)惯性坐标系SI-OXIYIZI。这里将SI选为前面定义的地面坐标系Sg。
2)视线(LOS)坐标系SLOS。文章所研究导引立足于视线坐标系,且将战机视为质点,视线坐标系原点O在战机质心上,OxLOS轴方向指向目标,与视线方向一致;OzLOS轴在垂直平面内指向上,并且与OxLOS轴正交;OyLOS轴方向根据右手定则确定。
3)战机航迹坐标系SkR。原点O在飞机质心上,OxR方向与战机速度矢量VR方向一致。
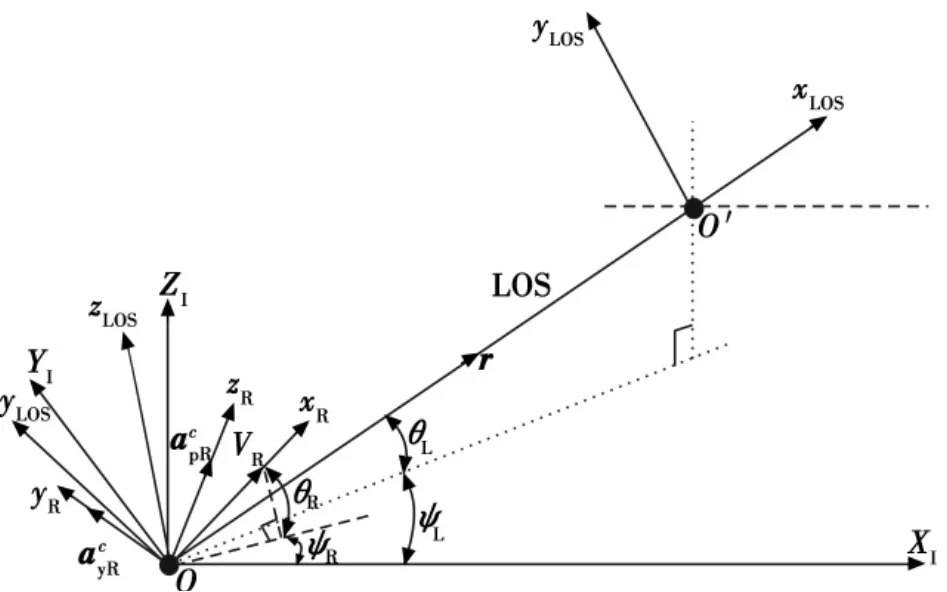
图1 远距引导涉及的坐标系图Fig.1 Coordinate systems for long-distance navigation
上述各个坐标系如图1所示。下标R代表我方战机;VR表示战机的速度矢量;r表示战机到目标空域的距离矢量;ψL,θL分别表示视线偏航角和视线俯仰角;ψR,θR分别表示战机航迹偏航角和航迹俯仰角分别表示战机的偏航加速度和俯仰加速度,下标p,y分别表示俯仰和偏航。
根据上面涉及的坐标系之间的关系可以得到战机相对指定空域的三维运动方程为[7-8]
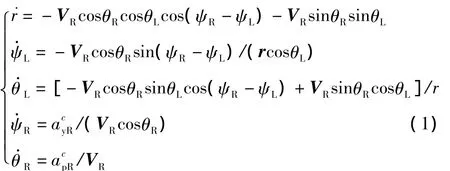
其中:r,ψL,θL,θR,ψR,,为变量为控制量,需设计适当的来使引导控制战机到达指定的空域。此时,有7个变量只有5个方程,需要建立关于控制量设计的方程,即导引模型的建立。
2 攻击机导引模型的建立
比例导引律是目前国内外研究较早,也比较成熟的导引律。它使飞行器速度矢量的旋转角速度与目标视线的旋转角速度成正比。主要优点是轨迹比较平直,技术上容易实现,所以被广泛应用。不同的比例导引律有不同的表达形式[9],一般的表达式如式(2)所示。

式中:N是导引常数;ΩLOS是视线角速度矢量。L随着不同的比例导引形式而不同,对于纯比例导引(PPN),其表达式为

式中:eR=[cosθRcosψR-cosθRsinψR- sinθR]T,aR,VR分别表示我方战机的加速度和速度矢量。
由于PPN以追踪器速度矢量为参考基准,实现起来比较简单,捕获域较大,所以选择纯比例导引(PPN)作为战机的远距引导律进行研究。
在战机进入指定区域时,一般是指离敌机较近的区域,根据战术及作战经验,要求战机以一定的方位角进入,保持最佳的攻击位置及对敌机角度上的优势。当我战机进入指定区域时,很容易被敌机发现,这时战机在角度上的优势十分必要,可以随时进行攻击,该角度即终端进入角通过设计偏置项来约束。
带进入角约束的三维纯比例导引(3DPPN/EAC)的基本矢量形式可定义为[10]
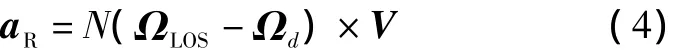
式中:Ωd就是为了约束终端进入角而加的偏置项;ΩLOS负责使战机速度方向与视线方向之间的偏差为零,也就是为了能够拦截目标;第二项Ωd的目的就是使实际视线角与期望视角的偏差为零,也就是为了使战机能够达到期望的进入角,在视线的俯仰或偏航平面内,期望角与视线角之间的关系如图2所示。
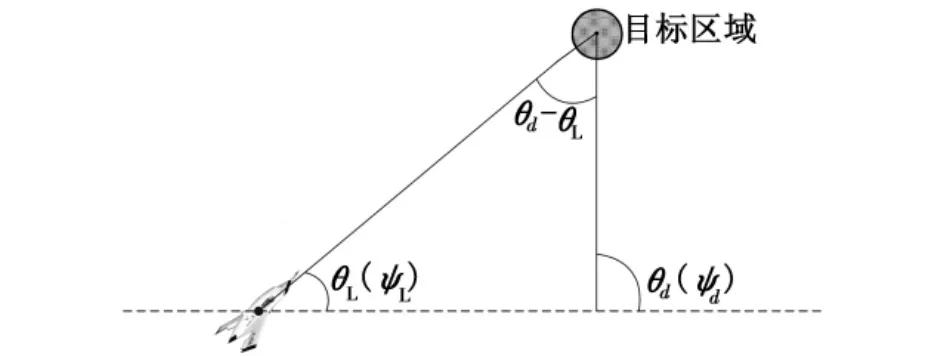
图2 期望角θd(ψd)与视线角θL(ψL)之间的几何关系Fig.2 Geometric relationship of θd(ψd)and θL(ψL)
对于视线俯仰平面为

式中:θd是期望的进入俯仰角;ψd是期望的进入偏航角;η是一个任意的正常值,剩余时间为达到期望视线角的平均角速度,并代入到式(5)得:
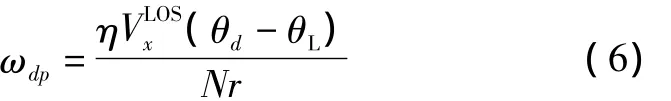
同样对于视线偏航平面为
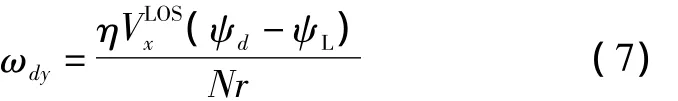
所以,Ωd可表示为
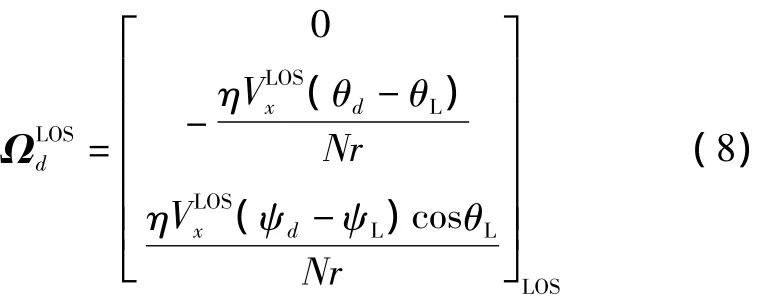
与PPN导引律一样,为了进行航迹计算与仿真,需要推导3DPPN/EAC指令加速度的标量形式。以便于构成闭合的方程组,进行航迹的求解与分析。
将指令加速度在战机航迹坐标系下分解可表示为

式(10)~式(12)的转换矩阵由各种坐标系之间的转换关系确定。结合式(1)组成闭合的方程组,从而解得各个变量。
3 仿真与结果分析
为了使战机进入指定空域时保持一定的态势优势,按照一般作战要求,取自动导引阶段的初始相对距离为r=10 km,战机的初始速度为V=170 m/s,取进入时偏航角为0°(从后向前攻击),俯仰角为-30°(从上向下攻击)。在Matlab7.0下的仿真曲线如图3~图8所示。
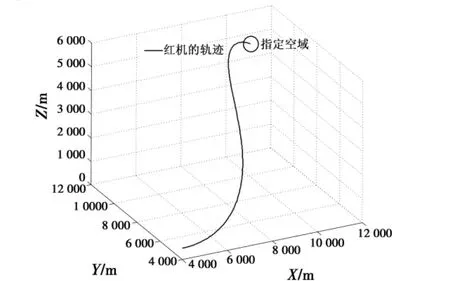
图3 三维轨迹曲线图Fig.3 The 3D trajectory curve

图4 各过载曲线图Fig.4 Curves of different overloads
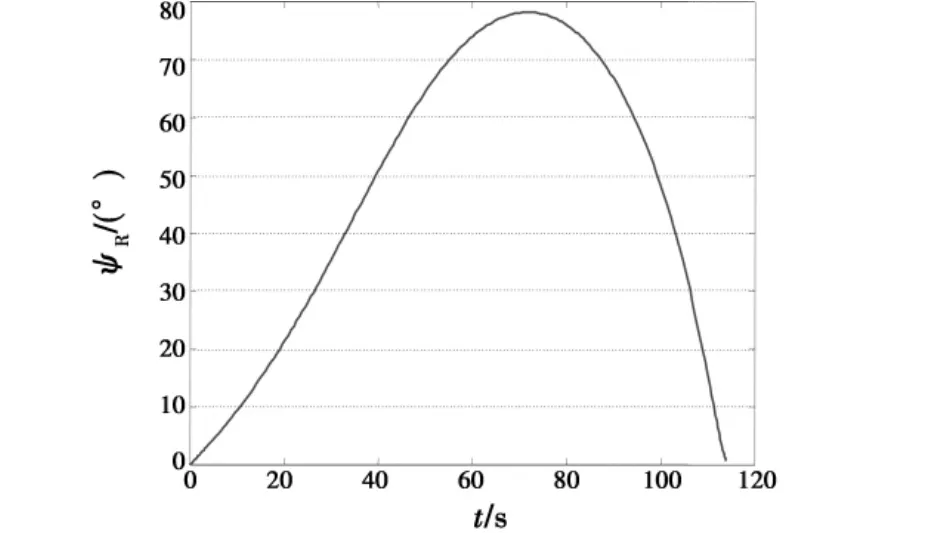
图5 视线偏航角ψR的曲线图Fig.5 Curve of LOS yaw ψR

图6 视线俯仰角θR的曲线图Fig.6 Curve of LOS pitch θR
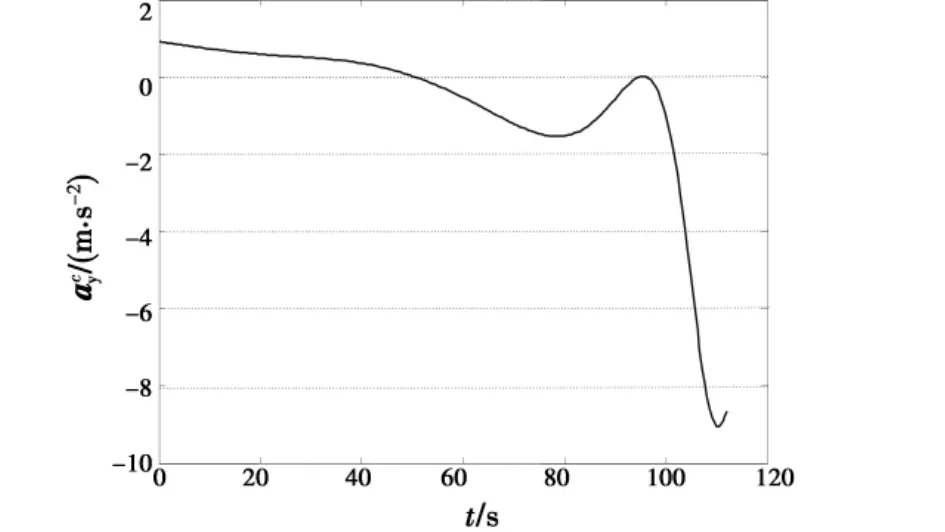
图7 偏航指令加速度曲线图Fig.7 The yaw acceleration
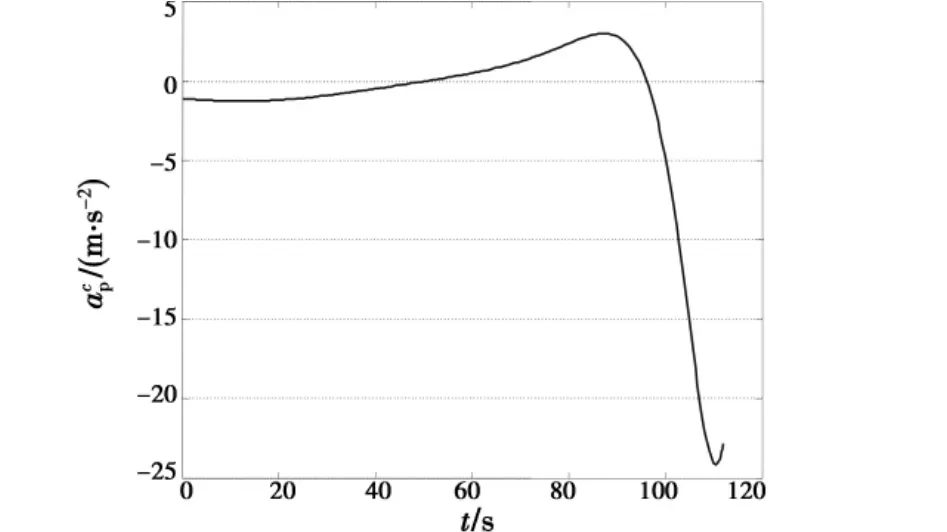
图8 俯仰指令加速度曲线图Fig.8 The pitch acceleration
结果分析:由图3可知,带进入角约束的三维纯比例引导的方法可以有效引导战机进入指定空域;由图5可知,战机进入指定空域的偏航角约为0°;由图6可知,战机进入指定空域的俯仰角约为30°,且为向下攻击状态,离预先设定的要求偏差十分细小,对态势的影响可以忽略,表明达到了预期的战术优势;由图3、图7~图8可知,过载、指令角速度也在攻击机接受范围之内。
4 结束语
本文主要研究了战机的远距引导方法设计问题。首先介绍了战机指挥引导方法的基本原理方法;然后根据远距引导的特点,在三维空间中研究了纯比例导引律,建立了三维空间中质点相对运动模型,考虑战机在空战中的战术要求,对进入指定空域时,设计了带进入角限制的三维纯比例引导律,仿真结果表明该模型能引导战机至我方有利位置,做到了“跑赢在起点”。
[1]吴文海,刁军,盛飞.现代战机导引系统及其关键技术[J].飞行力学,2004,22(4):1-4.
[2]于雷,李言俊,欧建军.现代战机最佳导引算法研究[J].航空学报,2006,27(2):314-316.
[3]杨春泉,倪世宏,吴文海.现代战机的导引及其控制律仿真研究[J].系统仿真学报,2004,22(4):999-1002.
[4]聂永芳,周卿吉,张涛.制导规律研究现状及展望[J].飞行力学,2001,19(2):7-11.
[5]吴文海,曲建岭,王存仁.飞行器比例导引综述[J].飞行力学,2004,22(2):1-5.
[6]杨军,杨晨,段朝阳,等.现代导弹制导控制系统设计[M].北京:航空工业出版社,2005:10-60.
[7]SRIVASTAVA R,SARKAR A K,GHOSE D,et al.Nonlinear three dimensional composite guidance law based on feedback linearization[C]//AIAA Guidance,Navigation,and Control Conference and Exhibit,2004:1-11.
[8]KIM Yongmin,SEO J H.The realization of the three dimensional guidance law using modified augmented proportional navigation[C]//Proceedings of the 35th Conference on Decision and Control,1996:2720-2712.
[9]JAE-HYUK OH,IN-JOONG HA.Capturability of the 3-dimensional pure PNG law[J].IEEE Transactions on aerospace and electronic systems,1999,35(2):491-503.
[10]RYOO C K,CHO H,TAHK M J.Time to go weighted optimal guidance with impact angle constraints[J].IEEE Transactions on control systems technology,2006,14(3):483-492.
