非高斯系统下卡尔曼滤波算法误差性能分析
2010-08-05陈金广马丽丽
陈金广, 马丽丽
(西安工程大学计算机科学学院,西安 710048)
0 引言
状态估计和滤波算法在自动化控制领域有着广泛的应用,尤其是上世纪卡尔曼滤波算法的出现对现代最优控制技术产生了深远影响[1-2]。卡尔曼滤波算法是针对线性高斯系统下的最小方差估计,对于非线性系统,可以采用扩展卡尔曼滤波等次优算法,此时状态估计结果为最小方差估计意义下的次优结果[3]。为了进一步提高滤波精度,Julier等人提出不敏卡尔曼滤波算法[4-5],采用确定性采样的方法对状态向量的后验概率进行估计,取得了较好的滤波效果,然而该算法时间复杂度有所增加。粒子滤波算法[6-8]采用随机采样的思想,利用大量的粒子对状态估计的后验概率进行逼近,能够解决非线性非高斯系统状态估计的问题。然而粒子滤波算法需要大量的粒子参与运算,存在时间复杂度高的问题。因此,在许多实时性较高的系统中仍然使用卡尔曼滤波。
卡尔曼滤波的一个使用条件是高斯系统,对于非高斯系统,算法的滤波结果误差是线性最小方差意义下的最优估计[2]。本文用仿真的方法探讨系统噪声在均值相同、方差相同的条件下,噪声的非高斯性对卡尔曼滤波算法误差性能影响程度的问题。此外,为了对噪声分布的非高斯程度实施量化,采用信息距离的方法对系统的非高斯程度进行度量。分别针对均匀分布、伽马分布和瑞利分布3种非高斯分布下的状态估计系统采用卡尔曼滤波算法进行滤波。仿真结果表明,在噪声均值和方差相同的条件下,尽管几种非高斯分布和高斯分布的信息距离大小不同,然而其滤波结果误差基本一致。这一结果是对非高斯系统下卡尔曼滤波内容的补充,对工程实践人员有一定的参考价值。
1 噪声分布模型
高斯分布是统计学中最常用的一个分布,它是描述围绕均值的一组数据集合,属于连续型分布,它是解决许多实际统计问题模型中的一个较为理想的统计模型。然而,现实世界往往存在一些不符合高斯分布的情形,常见的非高斯分布有均匀分布、伽马分布和瑞利分布等。下面简单介绍这些非高斯分布的概率密度函数定义及其统计特性。
均匀分布描述的是在有效的数据区间上,数据的取值概率相等。假如在二维空间中,用两个参数a,b描述均匀分布的数据取值区间,一个是数值的上界,另一个是数值的下界。连续均匀分布概率密度函数为

伽马分布是连续型分布,是指数分布在等待时间模型中的应用。伽马分布的概率密度函数有两个参数,尺度参数λ-1和形状参数r,这两个参数都是正实数。当参数r是整数时,伽马分布其实就是指数分布的扩展形式。具体地说,如果某事件发生在参数为λ的泊松过程之后,则该事件发生一次时的等待时间服从指数分布exp(λ),如果r是一个任意的正整数,那么直到事件发生r次为止的等待时间就服从伽马分布Γ(r,λ)。伽马分布的概率密度函数为
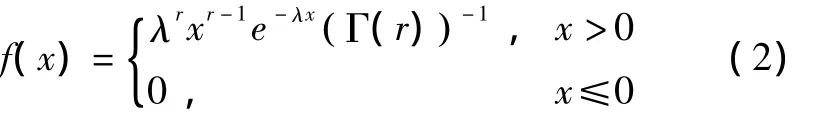
通常记作 Γ(r,λ)。伽马分布的均值为 rλ-1,方差为rλ-2。
瑞利分布的概率密度函数为
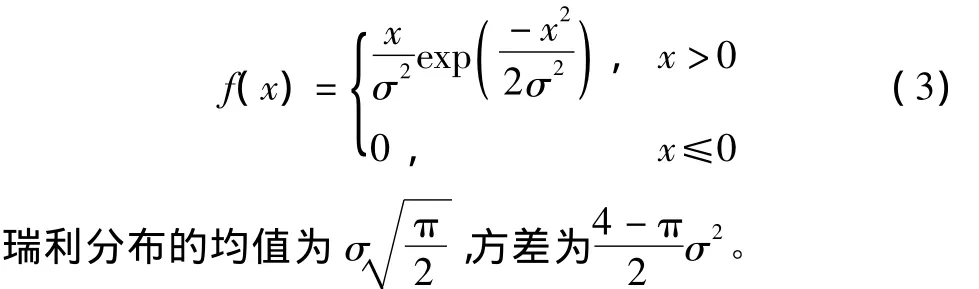
为了能够表示均值为0的噪声序列,将上述分布沿着x轴进行平移,使得上述各种分布的均值都为0。此时方差为10和方差为1000的概率密度函数如图1所示。从图1可以看出均匀分布、伽马分布、瑞利分布和高斯分布存在明显差异。
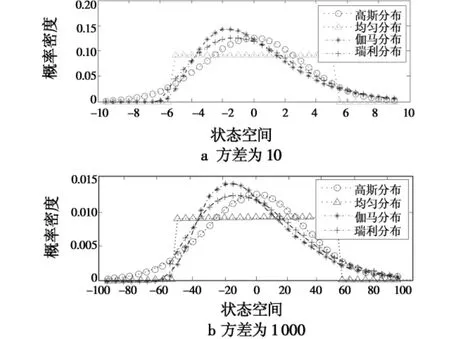
图1 几种常用分布的概率密度函数Fig.1 Probability density functions of several common distributions
2 基于信息距离的非高斯程度度量方法
对于两个不同概率分布之间距离的度量往往采用信息度量法。常用的有Kullback-Leibler距离、Topsoe距离、Chernoff距离和 Bhattacharyya 距离等[9-10]。为了考察各种非高斯分布的非高斯程度,采用信息距离的方法进行度量。
假如p0,p1表示两个分布的概率密度函数,它们之间的Kullback-Leibler距离定义为
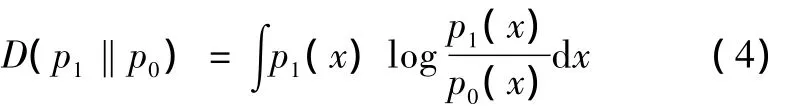
本文中log表示自然对数。
Chernoff距离定义为

依据上述定义,表1给出了均值为6.0496,方差为10情况下不同分布之间的4种信息距离度量。表1表明,几种分布的非高斯程度由大到小依次为瑞利分布、伽马分布、均匀分布。不同种类信息距离的度量方法计算出的值互不相同,因此,非高斯程度的强弱只有在相同的度量标准下进行比较才有意义。从信息距离的定义可知,如果两个概率分布完全一致,则其值为0,否则值不为0,而且随着非高斯程度的增加而增大。

表1 均值为6.0496,方差为10时的距离Table 1 Different distance with mean value of 6.0496 and variance of 10
3 仿真实验及结果分析
为了验证非高斯噪声分布对卡尔曼滤波结果误差的影响,假定系统是确定性系统(此时过程噪声为0),量测噪声服从高斯或者非高斯分布。下面两个例子分别采用线性系统和非线性系统进行仿真实验。
例1 线性系统滤波。
使用一维空间中的目标跟踪模型[11]。假设状态向量为x=[ξ]T,其离散线性系统的动态方程和量测方程分别为
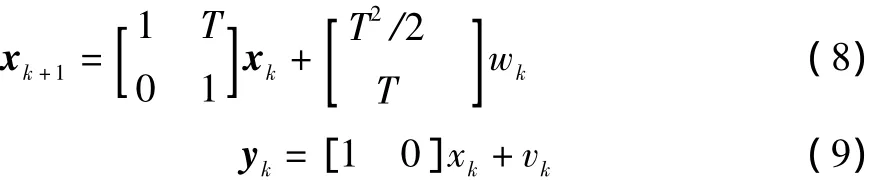
其中:wk,vk表示系统的过程噪声和量测噪声序列,它们服从均值为零方差为Q和R的某种分布。实验中参数设置如下:T=1,x(0)=[00]T;P0=diag(105);仿真步数N=300;分别采用均值为0和方差为10的高斯分布、均匀分布、伽马分布、瑞利分布产生量测噪声;采用蒙特卡罗方法仿真100次,计算不同分布噪声情况下滤波结果的均方根误差。此时,均方根误差定义为

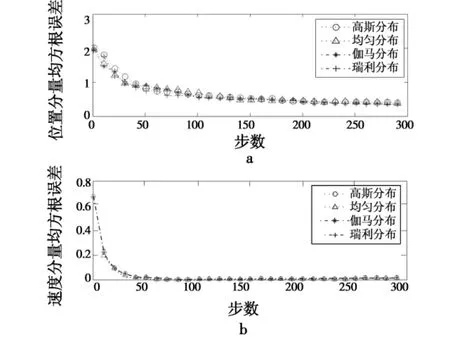
图2 噪声方差为10条件下位置和速度的均方根误差Fig.2 RMS of position and velocity with noise variance of 10
图2表明,高斯分布和非高斯分布产生的量测噪声对线性系统的滤波结果误差基本相同。
此外,为了考察不同非高斯分布噪声在方差水平不一样的条件下对滤波误差性能的影响,将过程噪声方差设置为0,而将量测噪声的方差作为变量(其取值集合设定为 R={10,30,50,…,1000})。在每个量测噪声方差取值的条件下,分别产生不同分布条件下的量测数据,对这4种情况分别进行滤波,计算结果的均方根误差。此时,均方根误差的计算公式为
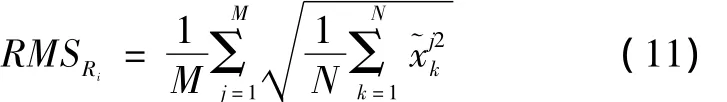

图3 不同方差水平下的均方根误差Fig.3 RMS under different variance levels
例2 非线性系统滤波。
采用经济学中使用的单变量非稳态模型,该模型是一个强非线性系统[6]。其离散非线性系统动态方程和量测方程为
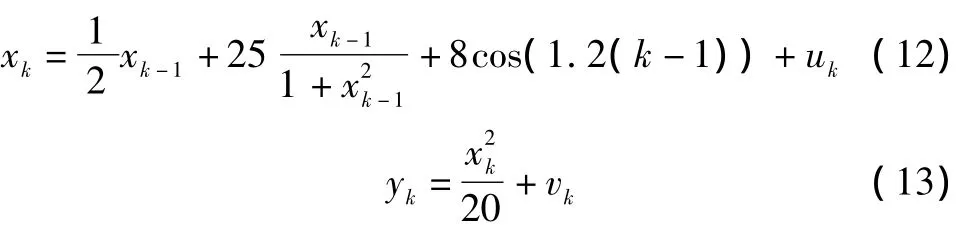
其中:uk,vk分别为系统的过程噪声和量测噪声序列,它们服从均值为0方差为Q和R的某种分布。实验过程中参数设置为:x0=1,P0=5,采用蒙特卡罗方法仿真100次,计算不同情况下滤波结果的均方根误差,均方根的计算公式与式(10)相同,结果如图4所示。图4表明,量测噪声在各类非高斯分布的条件下,其均方根误差与高斯分布的均方根误差基本一致。
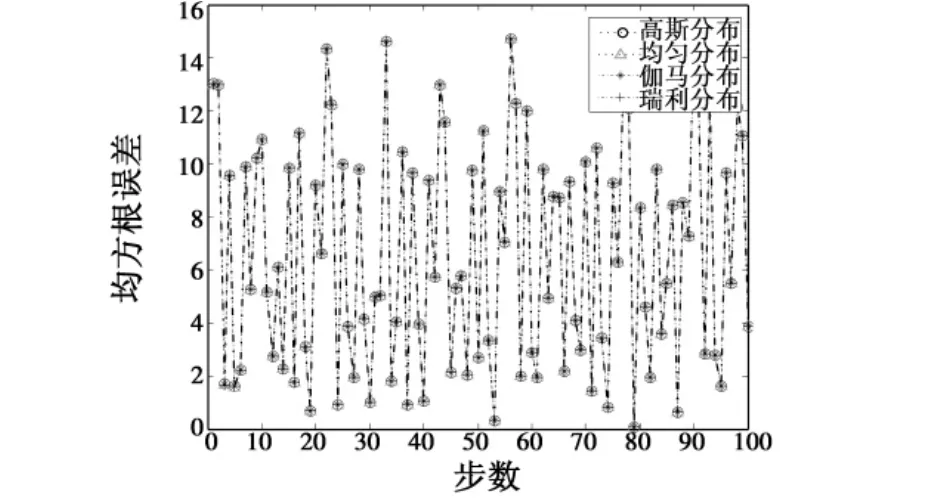
图4 噪声方差为10条件下的均方根误差Fig.4 RMS with noise variance of 10
为了考察滤波误差与噪声方差大小之间的关系,设定不同的噪声方差序列 R={10,30,50,…,1000},依次取不同的噪声方差仿真产生各种非高斯分布下的噪声序列,并采用扩展卡尔曼滤波算法获得滤波结果,根据式(11)计算估计值的均方根误差,结果如图5所示。图5表明,估计误差随着噪声方差的增加而增大;在不同的噪声水平上,各种非高斯分布的误差和高斯分布的基本一致。

图5 不同方差水平下的均方根误差Fig.5 RMS under different variance levels
上述两个例子仿真结果均表明,在噪声均值和方差一致的条件下,非高斯系统和高斯系统的滤波结果误差性能基本一致。而且,进一步仿真实验表明,当过程噪声取方差不为0的非高斯分布情况下,或者在过程噪声和量测噪声同时取方差不为0的非高斯分布情况下,线性系统或者非线性系统的滤波结果均方根误差都基本一致,这与上述实验结果相同。
4 结论
本文在已知噪声序列均值和方差的条件下,讨论具有均匀分布、伽马分布、瑞利分布3种非高斯分布对卡尔曼滤波误差性能的影响。采用计算非高斯分布和高斯分布之间信息距离的方法对非高斯程度进行度量。在均值和方差相同的情况下,尽管均匀分布、伽马分布和瑞利分布具有明显的非高斯特征,然而仿真实验结果表明非高斯系统和高斯系统的滤波结果误差性能基本一致。这就启示我们在工程应用中可以将非高斯程度较低的非高斯系统近似看作是均值方差相同的高斯分布,从而方便地利用卡尔曼或者扩展卡尔曼滤波算法加以解决。
[1]韩崇昭,朱洪艳,段战胜.多源信息融合[M].北京:清华大学出版社,2006.
[2]梁彦,潘泉,杨峰,等.复杂系统的现代估计理论及应用[M].北京:科学出版社,2009.
[3]王秋平,陈娟,王显利,等.光电跟踪系统几种次优非线性卡尔曼滤波性能比较[J].电光与控制,2008,15(3):10-13,28.
[4]JULIER S J,UHLMANN J K,DURRANT-WHYTE H F.A new method for the nonlinear transformation of means and covariances in filters and estimators[J].IEEE Trans on Automatic Control,2000,45(3):477-482.
[5]JULIER S J,UHLMANN J K.Unscented filtering and nonlinear estimation[J].Proceedings of the IEEE,2004,92(3):401-422.
[6]GORDON N,SALMOND D,SMITH A F M.Novel approach to nonlinear/non-Gaussian Bayesian state estimation [J].IEE Proceeding F Radar Signal Process,1993,140:107-113.
[7]OLIVIER C,SIMON J G,ERIC M.An overview of existing methods and recent advances in sequential Monte Carlo[J].Proceedings of the IEEE,2007,95(5):899-924.
[8]曲从善,许化龙,谭营.非线性贝叶斯滤波算法综述[J].电光与控制,2008,15(8):64-71.
[9]MAHESH V,MONICA F B,Petar M D.Performance comparison of Gaussian-based filters using information measures[J].IEEE Signal Processing Letters,2007,14(12):1020-1023.
[10]TOPSOE F.Some inequalities for information divergence and related measures of discrimination [J].IEEE Trans on Information Theory,46:1602-1609,2000.
[11]BAR-SHALOM Y,Li X R,Kirubarajan T.Estimation with applications to tracking and navigation[M].New York:Wiley-Interscience,2001.
