机载双基地雷达距离模糊杂波抑制方法性能研究
2010-08-05张柏华谢文冲王永良张永顺
张柏华, 谢文冲, 王永良, 张永顺
(1.空军工程大学导弹学院,陕西 三原 713800;2.空军雷达学院重点实验室,武汉 430019)
0 引言
空时自适应处理(STAP)是机载雷达的一项关键技术,对该技术的研究已进行了三十多年,主要是围绕单基地机载雷达展开的,STAP技术的主要目的是实现机载雷达对杂波和干扰的有效抑制[1]。近年来STAP技术在机载双基地雷达中的应用已成为雷达领域的热点研究方向。
双基地雷达由于在雷达“四抗”方面的潜在优势在近年来得到快速发展和广泛的应用,也是当今雷达研究领域的一大热点[2]。在单基地雷达空时自适应处理技术逐渐走向成熟和进入工程化的同时,人们很自然地把目光投向了双基地空时自适应处理的研究。机载双基地雷达工作时由于载机的运动、雷达的下视工作和收发分置,使得雷达接收的地杂波明显增强,且有多普勒频移和距离相关性。双基地机载雷达表现出更复杂的杂波特性,杂波呈现严重的非均匀性,使得双基地机载雷达的杂波抑制难度增大,特别是如果加上距离模糊的影响,抑制杂波的难度将进一步加大。
为了克服杂波非均匀特性对机载双基地STAP运动目标检测性能的影响,近几年一些学者提出了诸如多普勒翘曲[3](DW)、高阶多普勒翘曲[4](HODW)、角度 - 多普勒补偿[5](ADC)、基于配准补偿[6](RBC)、自适应补偿[7-9]、逆协方差矩阵线性预测[10-11](PICM)、空时内插[12](STINT)、基于配准的非均匀采样补偿[13](RBNFS)等方法。其中,DW 方法实现简单,但是它仅仅在多普勒域补偿了主瓣杂波谱中心,整体杂波谱并没有完全得到补偿;HODW方法性能比DW方法有一定程度改善,但是存在傅里叶变换导致的“篱笆栅格”现象;ADC方法在角度-多普勒域进行杂波谱中心补偿,但是需要利用惯导提供的系统参数,当系统参数存在误差时ADC方法性能严重下降;RBC在理想情况下能得到很好的性能,但是杂波谱峰值的估计精度、计算量及方法的鲁棒性不容忽视;自适应补偿虽然不需知道配置参数,在理想情况下性能也很好,但是实际中每个距离门数据的协方差数据极不稳定,导致性能下降很多;PICM方法虽然无需知道飞行和配置参数,但需要额外增加很多计算量;STINT方法与RBC方法类似,只是把杂波谱搬移到一个虚拟的位置;RBNFS方法在角度-多普勒域通过非均匀采样提取杂波谱中心,并利用最小二乘估计杂波谱中心的幅度,完成对非均匀杂波的补偿。上述方法均未考虑杂波距离模糊的影响。本文首先分析了存在距离模糊时的双基地机载雷达杂波分布特性,考虑到篇幅,只选择了DW,ADC和RBNFS三种典型机载双基地雷达距离非均匀补偿方法在两种机载双基地配置下的抑制距离模糊杂波的性能进行研究比较,最后给出了有益的结论。
1 机载双基地雷达杂波模型
图1给出了机载双基地雷达在任意几何配置下的几何关系,其中VT,VR分别是发射、接收平台载机的飞行速度;ψT,ψR分别是地面杂波散射点相对于发射、接收平台飞行方向的锥角,本文假设雷达天线都是正侧面放置,所以ψT,ψR也分别是发射、接收天线轴向与地面杂波散射点的锥角;θT,θR分别是发射、接收雷达天线波束指向相对于基线方向的方位角;δT,δR分别是发射、接收平台载机飞行方向相对于基线方向的方位角;φT,φR分别是杂波散射体相对于发射、接收平台天线轴向的俯仰角;hT,hR分别是发射、接收平台载机的飞行高度;L是双基地基线长度;RS是双基地探测距离和;RR和RT分别是接收机和发射机到杂波点的距离。

图1 机载双基地几何配置关系图Fig.1 The geometry configuration for airborne bistatic radar
由图1可以得到机载双基地雷达接收回波的多普勒频率为
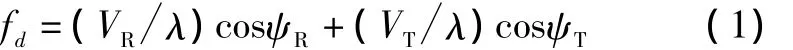
其中:

假设天线为正侧面放置,则 δT,δR均为0,由图1的几何三角关系可推出如下公式:
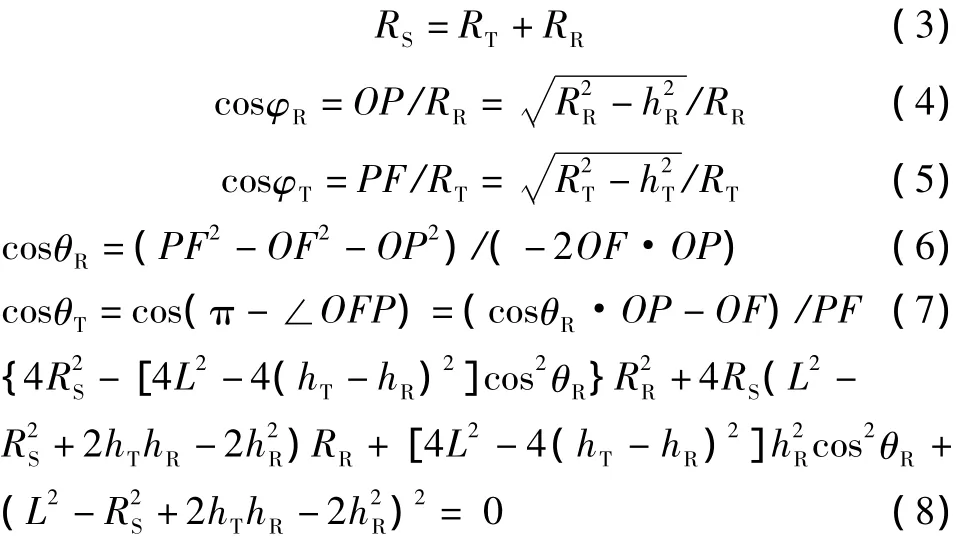
从式(8)可解出RR,然后将上述公式代入式(1)、式(2)便可得到接收回波的多普勒频率fd关于参变量θR的依赖于接收机空间锥角和双基地探测距离和两个变量的函数表达式如下:

需要指出的是,式(8)中RR有两个解:式(10),当 π/2≤θR≤3π/2 时,取加号;当 θR≤π/2 或 θR≥3π/2,取减号。通过仿真,便可以得到任意几何配置、载机任意飞行方向、天线任意安置条件下,接收平台锥角-地杂波多普勒的二维图。
2 机载双基地雷达存在距离模糊时的杂波谱特性
为了分析方便,本文选择了图2的两种典型配置进行了仿真,其中接收、发射天线均为正侧面放置。仿真具体参数为:阵元数N=8,脉冲数K=16,杂噪比60 dB,基线距离为80 km,双基地距离和为130 km,发射载机和接收载机高度均为8 km,飞行速度均为140 m/s,工作波长 λ=0.23 m,脉冲重复频率 fr=2434.8 Hz,最大作用距离400 km,此时,有3个模糊距离:130 km,53.21 km,76.42 km,考虑到天线背面的辐射很弱,在此没有考虑,假定脉冲追赶准确同步,接收主波束指向阵面法向。
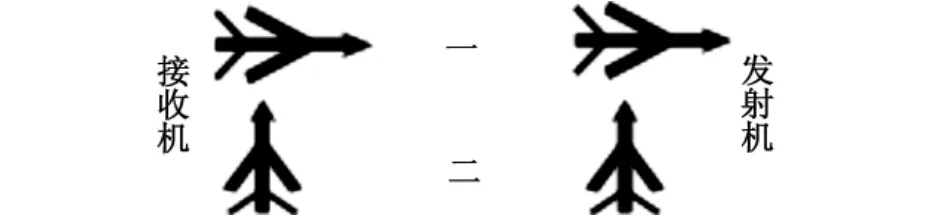
图2 两种典型配置情况图Fig.2 Two typical configurations
图3~图6给出了典型配置一、二不存在距离模糊和存在距离模糊时的杂波特征谱和功率谱等高线图。
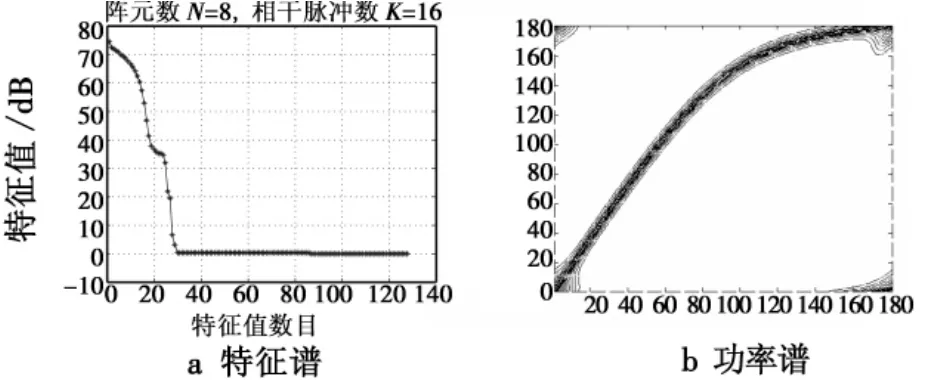
图3 配置一不存在距离模糊的情形Fig.3 Configuration 1 without range ambiguity
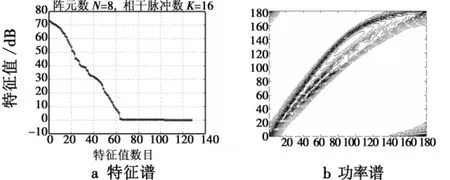
图4 配置一存在距离模糊的情形Fig.4 Configuration 1 with range ambiguity
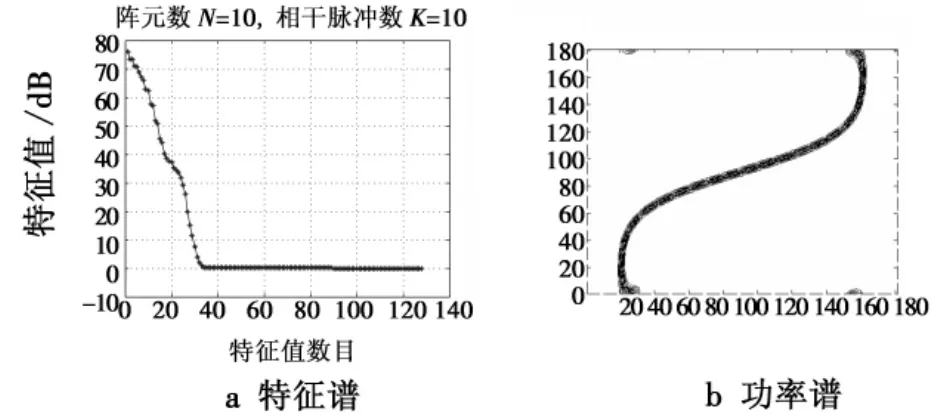
图5 配置二不存在距离模糊的情形Fig.5 Configuration 2 without range ambiguity

图6 配置二存在距离模糊的情形Fig.6 Configuration 2 with range ambiguity
从图中可以看出:一方面,当存在距离模糊时杂波协方差矩阵的大特征值个数(即:杂波自由度)大大增加,杂波自由度从30左右增加到60多,其中配置二时比配置一时略微多一点;另一方面,杂波功率谱也由于距离模糊而大大展宽。以上两种因素给传统STAP方法的杂波抑制性能带来了很大的影响。
3 机载双基地雷达存在距离模糊时典型补偿方法的性能仿真与分析
本节以3DT方法为例对DW,ADC和RBNFS 3种方法在图2配置一、二时存在三重距离模糊时的性能进行比较。其中,DW,ADC和RBNFS等3种补偿类方法均是首先对回波数据进行补偿处理,然后再通过3DT方法进行杂波抑制处理,仿真参数同上节。为了避免出现矩阵奇异现象,RBNFS方法中利用最小二乘准则估计杂波幅度时进行了对角加载,加载量为0.01。
图7~图10给出了配置一时不补偿以及经DW,ADC,RBNFS方法3种补偿后的杂波特征谱和功率谱等高线图(理想情况下杂波特征谱、功率谱等高线图见上节图4、图6)。
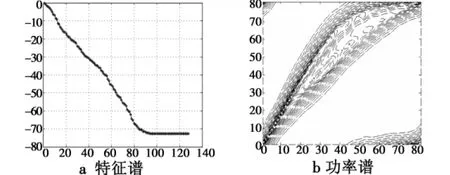
图7 配置一未补偿情形Fig.7 Configuration 1 without compensation

图8 配置一DW方法补偿Fig.8 Configuration 1 using DW method
其中,理想情况下的杂波协方差矩阵由矩阵直接生成,不补偿和3种补偿方法由邻近距离门样本经训练得到。从图中可以看出,由于存在距离模糊,即使理想情况下杂波自由度(即:大特征值个数)也远多于单基地正侧面时的N+K-1(23)个,达到60以上;不补偿时杂波大的特征值个数最多,达到80以上,其杂波功率谱也展宽最多;经DW和ADC补偿后,大的特征值个数略有降低,杂波功率谱展宽也有所改善;经RBNFS补偿后大特征值个数和杂波功率谱宽度就和理想情况下很接近了。
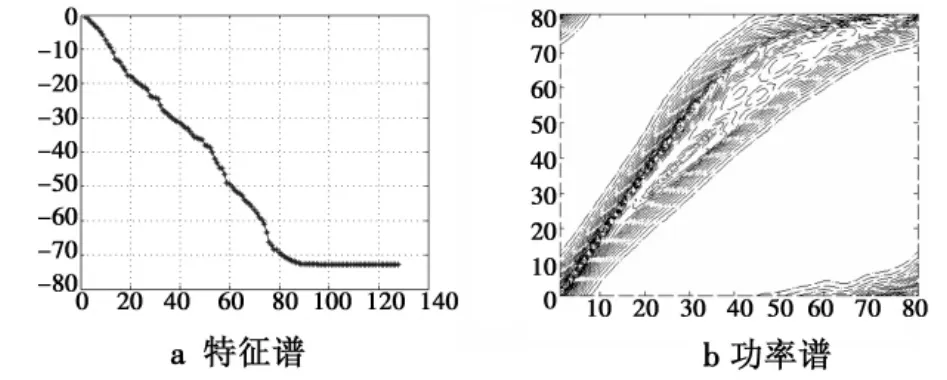
图9 配置一ADC方法补偿性能Fig.9 Configuration 1 using ADC compensation method

图10 配置一RBNFS方法补偿性能Fig.10 Configuration 1 using RBNFS compensation method
图11~图14给出了配置二时不补偿以及经DW,ADC,RBNFS方法3种补偿后的杂波特征谱和功率谱等高线图。从图中可以看出,相对配置一,配置二时理想情况下的大特征值个数又增加很多,达到80以上,杂波功率谱相对配置一也复杂很多,这说明双基地配置是影响杂波特性的重要因素;不补偿时的大特征值个数则达到了100以上,经DW,DC补偿后性能有所改善;经RBNFS补偿后的性能亦没有配置一时的改善明显。
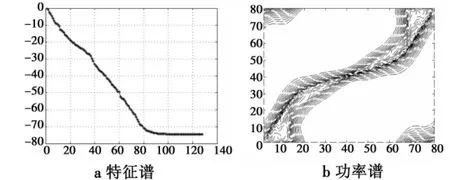
图11 配置二未补偿情形Fig.11 Configuration 2 without compensation

图12 配置二DW方法补偿Fig.12 Configuration 2 using DW compensation method
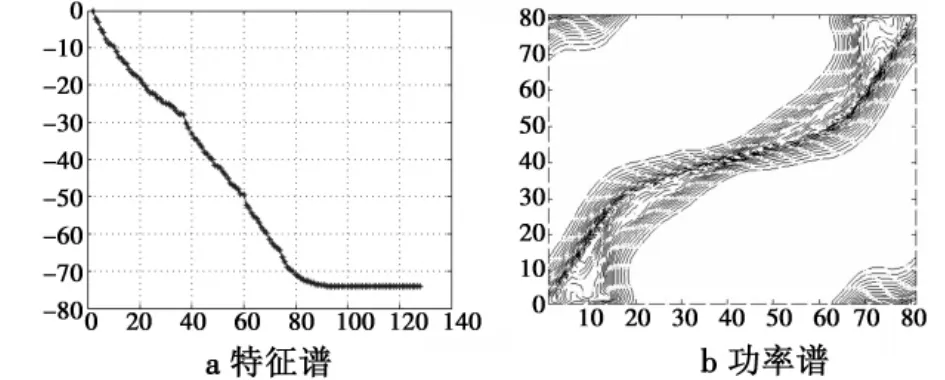
图13 配置二ADC方法补偿Fig.13 Configuration 2 using ADC compensation method

图14 配置二RBNFS方法补偿Fig.4 Configuration 2 using RBNFS compensation method
图15、图16给出了配置一、二不存在和存在距离模糊时的不补偿和3种补偿方法的STAP改善因子比较图。从图中可以看出:一方面,由于存在距离模糊,3种典型补偿类STAP方法的主杂波凹口区相对没有距离模糊时均存在一定程度的展宽,不补偿时尤为明显;另一方面,当存在距离模糊时,3种典型补偿类STAP方法中DW和ADC的杂波抑制性能下降较为明显,而RBNFS方法仍能保持较好的杂波抑制性能。
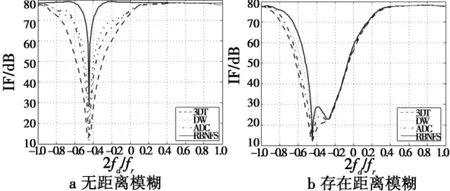
图15 配置一补偿类STAP方法改善因子比较Fig.15 IF for compensating method of STAP in configuration 1
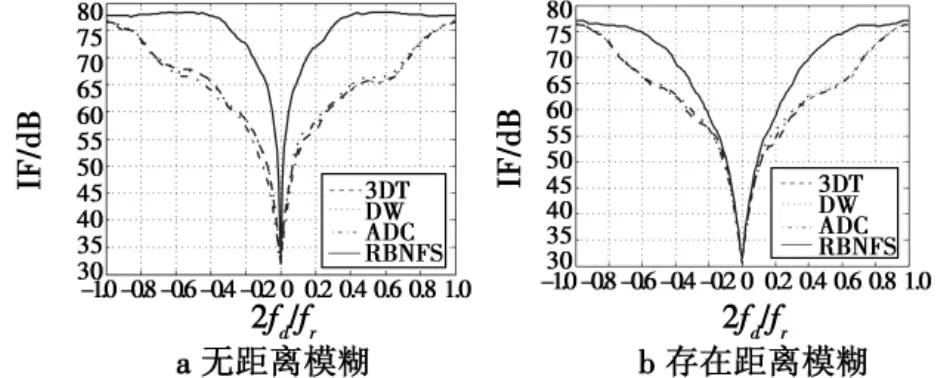
图16 配置二补偿类STAP改善因子比较Fig.16 IF for compensating method of STAP in configuration 2
4 结论
本文基于机载双基地雷达杂波模型,分析了机载双基地雷达杂波谱在距离模糊情况下的空时分布特性,并对机载双基地雷达存在距离模糊时典型补偿类STAP方法的杂波抑制性能进行了分析。通过仿真分析可以看出,机载双基地雷达配置下距离模糊对传统STAP方法的杂波抑制性能影响很大,现有的双基地机载雷达补偿类STAP方法在存在距离模糊时性能改善受到一定程度的限制,相对而言,RBNFS方法的杂波抑制性能较好。下一步的主要工作将是研究存在距离模糊情况时的有效的机载双基地雷达STAP杂波抑制方法。
[1]王永良,彭应宁.空时自适应信号处理[M].北京:清华大学出版社,2000.
[2]杨振起,张永顺,骆永军.双(多)基地雷达系统[M].北京:国防工业出版社,1998.
[3]BORSARI G K.Mitigating effects on STAP processing caused by an inclined array[C]//Proc of the IEEE National Radar Conf,Dallas,TX,USA,1998:135-140.
[4]PEARSON F,BORSARI G.Simulation and analysis of adaptive interference suppression for bistatic surveillance radars[C]//Proc of the Adaptive Sensor Array Processing Workshop,Lincoln Laboratory,MA,USA,2001:1-21.
[5]HIMED B,ZHANG Y H,HAJJARI A.STAP with angle-Doppler compensation for bistatic airborne radar[C]//Proc of the IEEE National Radar Conf,Long Beach,CA,USA,2002:311-317.
[6]LAPIERRE F D,VERLY J G.Registration-based solutions to the range-dependence problem in STAP radars[C]//Proc of the Adaptive Sensor Array Processing Workshop,Lincoln Laboratory,MA,USA,2003:1-6.
[7]JAFFER A,HO P T.Adaptive angle-Doppler compensation techniques for bistatic STAP radars[R].Final Technical Report,AFRL-SN-RS-TR-2005-398,2005.
[8]MELVIN W L,DAVIS M E.Adaptive cancellation method for geometry-induced nonstationary bistatic clutter environments[J].IEEE Trans Aerosp Electron Syst,2007,43(2):651-672.
[9]LAPIERRE F D,RIES P,VERLY J G.Foundation for mitigating range dependence in radar space-time adaptive processing[J].IET Radar Sonar Navigation,2009,3(1):18-29.
[10]LIM C H,MULGREW B.Prediction of Inverse Covariance Matrix(PICM)sequences for STAP[J].IEEE Signal Processing Letters,2006,13(4):236-239.
[11]LIM C H,ABOUTANIOS E,MULGREW B.Linear prediction of rang-dependent inverse covariance matrix[C]//Proc of the National Radar Conf,Verona,NY,2006:228-232.
[12]VARADARAJAN V,KROLIK J L.Joint space-time interpolation for distorted linear and bistatic array geometries[J].IEEE Transactions on Signal Processing,2006,56(3):848-860.
[13]XIE Wenchong,WANG Yongliang.Range-dependence compensation method for bistatic STAP radar[C]//2008 IEEE Congress on Image and Signal Processing,2008,5:503-506.
