新的非相干UWB 系统平均性能的理论计算方法

杨志华，王野，张钦宇，王宇峰，刘宁宁，张乃通

(1.哈尔滨工业大学 深圳研究生院 通信工程研究中心，广东 深圳 510085；2.总参通信部驻深圳地区 军事代表室，广东 深圳 518001；3.中国电子系统设备工程公司研究所 通信一室，北京 100039)

1 引言

UWB(ultra wideband)技术以其小尺寸、低功率、低成本等优点在中低速通信，如传感器网络、目标定位、辨识系统等领域受到广泛关注[1]。而低复杂度的接收机设计是超宽带技术得以广泛应用和发展的关键问题。目前，针对超宽带接收机的研究主要集中于基于相干方式的Rake[2]接收机、基于非相干方式的 TR(transmitted reference)[3]接收机和ED(energy detection)[4～6]接收机 3 种方案。Rake 接收机通过对超宽带信号多径能量的相干分集接收，性能要优于其他2种，但是对于系统实现，大量的支路花费、复杂的信道估计技术以及对同步性能的高敏感性等问题导致接收机的复杂度难以承受；TR方式的接收机采用发送参考信号的方式，有效地避免了信道估计带来的系统复杂度，但是由于采用相关积分，对接收机的同步性能仍然比较敏感，接收机需要具有精确的延时单元，导致成本上升，同时，由于需要参考信号作为模板，浪费了发射信号的能量。ED方式的接收机，不需要模板和信道估计而直接提取接收信号能量，大大减少了接收机复杂度，同时对同步误差的精度要求比较低[7]，所以这种方式实现最简单、成本较低，对于某些应用具有较高参考价值，为脉冲超宽带技术的推广带来了方便。

平均误码率是评价超宽带接收机在无线衰落信道下的常用性能指标，如文献[8]对Rake接收机的性能进行的分析，但数学计算复杂，其中对Rake接收机合并的多径数量假定为确定量，这在随机信道中是不准确的。目前针对超宽带能量检测接收机的此项性能指标少有深入研究，主要是由于超宽带密集多径信道复杂的特性，大量多径以簇的形式在接收端随机到达，接收机需要在一定时间窗口内收集多径能量实现解调，导致在平均误码率计算时处理的随机变量较多且关系复杂，大多数研究均采用Monte Carlo仿真分析[9～12]，理论计算方面研究较少。本文针对此问题，基于随机点过程模型对超宽带IEEE 802.15.3a信道模型[13]（以下简称标准信道模型）进行了完整的分析，给出了超宽带能量接收机窗口内信噪比（或者信道能量增益）的概率密度的有效逼近模型，从而能够推导出超宽带接收机在密集多径衰落信道下的平均误码率。

首先，第2节推导了超宽带非相干接收机平均误码率的数学表达式，并分析其存在的问题；第 3节针对上述问题，拟合出信道能量增益概率密度以及高阶统计量；第4节结合理论分析对仿真结果进行了讨论；第5节是结束语。

2 衰落信道下超宽带非相干系统的平均误码率

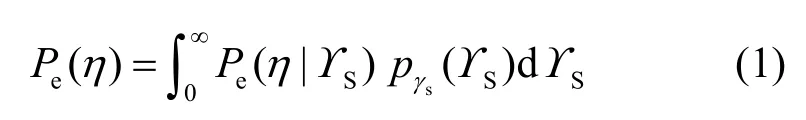
衡量衰落信道下接收机性能的重要评价标准为平均误码率，其定义为[14]其中，η为接收机判决门限，ϒS为接收窗口的瞬时信噪比。通过式(1)可知，平均误码率可以认为对接收机的条件误码率 Pe(η |ϒS)进行接收窗口内信噪比的统计平均，即信道能量增益的统计平均（噪声为确定的条件下）。实现此平均的方法有 2种，一是产生大量信道样本进行Monte Carlo仿真来实现。即对每个样本下的条件误码率进行计算，然后做算术平均。这种方法具有较高的复杂度，且误差难于控制；二是推导出能量增益的概率密度pγs(ϒS)，然后计算式(1)从而得到平均误码率的闭合表达式。本文则围绕第二种方法，首先来研究条件误码率的推导。

超宽带非相干接收机前端一个比特信号模型可以表示为

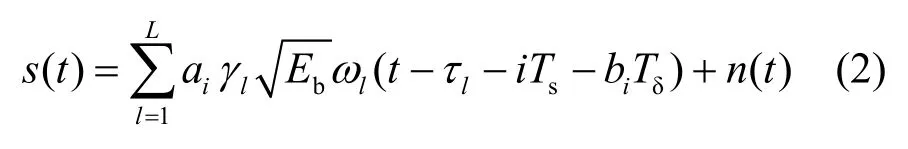
其中，L表示到达接收机前端的多径分量数目，ωl(t)表示第l条路径的接收波形，γl和τl分别表示第l条多径分量的幅度衰落和信道延迟参数，Eb为每比特能量，Ts表示信号的符号周期。n(t)表示加性高斯白噪声(AWGN)，其双边功率谱密度为 N0/2。当接收信号为OOK调制时，ai表示第i个传输比特，等概率取值为{0,1}，此时bi为0；当接收信号为PPM调制时，bi表示第 i个传输比特，等概率取值为{0,1}，Tδ表示PPM信号在时间轴上的调制位移，在 PPM 系统里，通常令Tδ=Ts/2，此时ai为 0。接收信号经过带宽为B的带通滤波器，以滤除带外噪声。不失一般性，假定每个调制符号中只包含一个脉冲，这很容易推广到多个脉冲的情况。并且假定信号的脉冲重复周期远大于信道的时延拓展，无须考虑符号间干扰(ISI)的影响。

接收机的结构框图如图1所示。

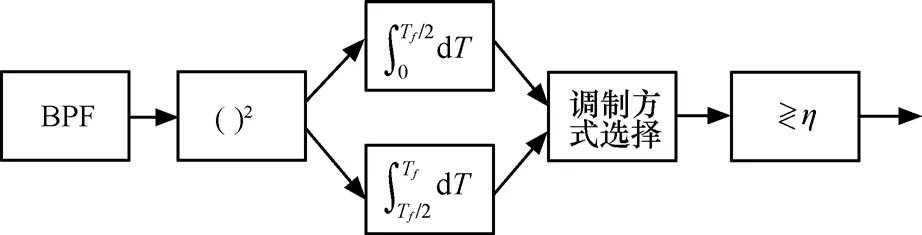
图1 非相干接收机结构框图

首先，信号经过带通滤波器、平方律检波器，然后进入区间积分器，联合形成对比特周期内接收信号的采样。调制方式的选择可以通过对积分后的信号处理获得。当采用OOK调制方式时，调制方式选择模块为加法器，当采用 PPM 调制方式时，调制方式选择模块为减法器。最后信号通过与判决门限η的比较得到比特流的输出。

由文献[15]，利用高斯分布近似χ2分布，得到OOK调制方式下的条件误码率为

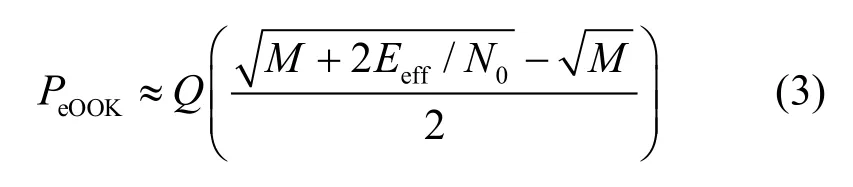
当接收信号为 PPM 调制时，同样利用高斯分布近似的方法可得接收机的最佳门限为 0，相应的条件误码率为

对比OOK调制和PPM调制方式的条件误码率可知，二者之间尽管有所区别，但是比值是一个由比特采样点数 2M 以及输出信噪比 Eeff/N0共同决定的变量。为了比较二者的性能，定义条件误码率比例因子

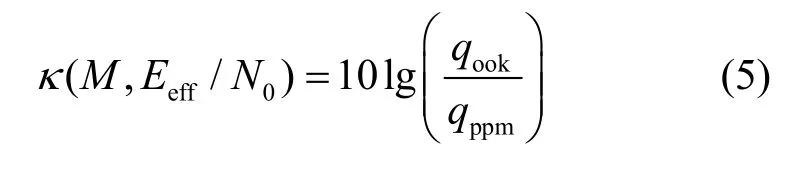
其中，qook和qppm分别为OOK调制方式下和PPM调制方式条件误码率函数Q函数的自变量。给出了该比例因子随信噪比和M变化的曲线，如图2所示。在相同的M条件下，当信噪比增大时，比例因子绝对值逐渐减小，PPM调制方式的优势随信噪比的增加而减少。且当M大于100时，PPM和OOK调制方式的条件误码率性能差异趋于常数（比例因子约为-3.5）。

图2 PPM调制与OOK调制误码率性能比例因子

上述结果表明，PPM调制相对于OOK调制的条件误码率增益具有一定的适用范围(见后文分析)，对于系统设计要慎重选择。

3 信道能量增益概率密度的近似求解

在获得了OOK和PPM调制方式下条件误码率式（3）和式（4）的基础上，只要求出信道能量增益的概率密度就可通过式（1）获得多径衰落信道下系统的平均误码率的表达式。在IEEE 802.15.3a多径衰落信道下，密集多径分量出现在接收机处理窗口内，造成窗口内随机变量较多且关系复杂，以致信道能量增益的概率密度求解困难。本文则以随机点过程模型描述标准信道模型，建立起接收窗口内各个随机变量间的联系，解决信道能量增益概率密度求解中的难题。由于标准信道模型中簇到达和簇内多径均呈随机到达的特点，完全符合随机点过程中的簇生点过程模型，因此利用点过程的性质可以得到信道能量增益的均值和方差表达式[16]。

均值[16]：

方差：

其中，Φ为接收机窗口内的能量增益，K=exp{(σl n10/10)2}，σ及其他参数定义参考文献[13]，Ts为比特持续时间（为了收集所有多径能量对比特持续时间 Ts取极限）。具体推导过程见附录A。

基于所得能量增益的均值和方差，研究其概率分布。由信道模型的数学描述可知，信道能量实际上是大量对数正态分布的随机变量之和。数学上分析大量对数正态分布的随机变量记录之和存在很大困难[17]，随着分布参数的变化，该分布并不一定收敛于某一确定分布。目前有研究[18]将信道能量的统计分布近似成对数正态分布，也有研究[19]基于中心极限定理将其近似为高斯分布。本文分别采用二者来拟合信道能量的概率分布，通过若干数字特征对比拟合的效果，分析合理性，以及后续内容中利用接收机系统性能评估来验证其有效性。

首先，以随机变量的数字特征作为依据来衡量2种近似分布的合理性。

通常来讲，衡量2个概率密度之间差别的统计量，除均值和方差外，还有如下2种。

定义 1 三阶中心矩与标准差的立方之比称为随机变量概率密度的偏度系数。记作：

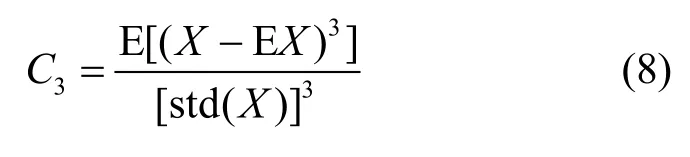
该系数反应了概率密度的对称情况。

定义2 四阶中心矩与标准差的4次方之比称为随机变量概率密度的峰度系数。记作：

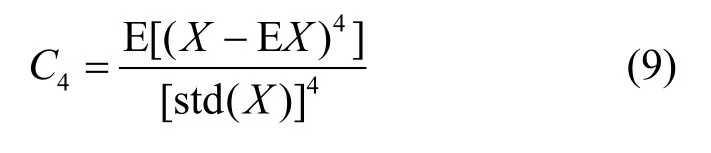
该系数反应了概率密度在均值附近的集中情况。

可以证明，对数正态分布和高斯分布的偏度系数和峰度系数分别可表示为

对数正态分布：

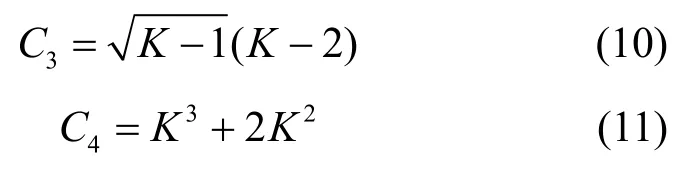
高斯分布：

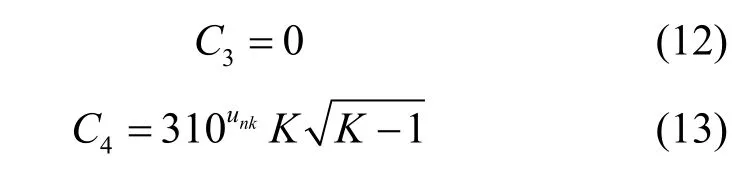
式（10）～式（13）具体推导过程见附录B和附录C。

表1给出了信道能量的概率密度拟合为对数正态分布条件下以及拟合为高斯分布条件下求得的数字特征，及基于IEEE 802.15.3a给出的修正S-V模型产生的信道冲激响应样本通过Monte Carlo仿真而求得的数字特征（表1中标明“仿真”字样），三者之间的对比结果。

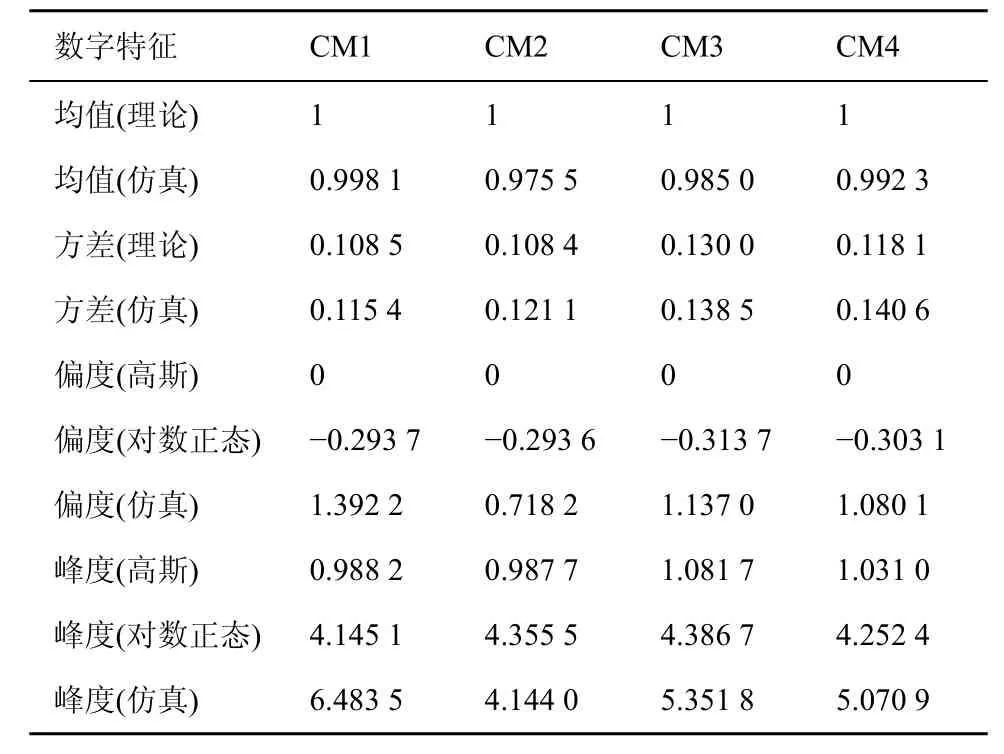
表1 信道能量的概率密度数字特征在不同条件下对比

从表1中可以看出：

① 理论推导出的均值和方差在 4种信道条件下都与实验结果符合的比较一致，验证了理论推导的正确性；

② 对于概率密度的偏度来说，4种信道条件下仿真实验的结果都具有较大的非对称性，而高斯分布与对数正态分布的偏度都与实验结果有较大的偏差，实验结果对称性较差；

③ 对于概率密度的峰度来说，4种信道条件下，实验结果与高斯分布差距较大，更接近于对数正态分布。

所以从上述数字特征来看，将多径能量的概率密度拟合为对数正态分布更具有合理性。

4 仿真实验和结果分析

为了验证本文对接收机平均误码率指标的推导，首先采用Monte-Carlo方法对信道能量的统计特性进行了计算机仿真，然后，分析采用参数法估计信道能量增益概率密度的合理性以及各种参数对概率密度的影响；验证拟合后的信道能量增益概率密度对于评价接收机在衰落信道下平均误码率的有效性；比较超宽带非相干接收机OOK调制方式与PPM调制方式平均误码率的性能。

仿真过程中，UWB信号采用宽度为1ns的高斯二阶导数脉冲，调制方式分别为OOK和PPM 2种；信道的观察时间取 400ns，大于最大多径时延拓展以避免码间干扰。每比特信号内的采样点数为2M=200。

1) 概率密度拟合分析。

结合前面对于信道能量增益的均值和方差的理论分析，利用Monte-Carlo方法分别对CM1～CM4这4组信道进行了仿真，结果如图3～图6所示。仿真中每组信道条件下取1 000组实现，并令首径的均值Ω0=1。

图3为CM1的情况，仿真结果与对数正态分布的结果吻合较好，与高斯分布的结果吻合较差。拟合误差主要出现在概率密度峰值附近。仿真曲线的峰度大于对数正态分布和高斯分布。故实际信道能量分布特性相对于均值的集中程度要高于对数正态分布和高斯分布。

图4为CM2的情况，仿真结果与对数正态分布以及高斯分布的结果吻合较差，但是相对于CM1而言，仿真结果有趋近于高斯分布的趋势，拟合误差同 CM1的情况相同，仍然出现在峰值附近。结合表1的结果，在四组概率密度中，CM2唯一出现对数正态分布峰度大于仿真结果的情况，其主要原因是CM2信道为非视距情况，簇到达率为4组信道情况中最大者，在400ns的观察时间内，平均簇到达数目大于 100，信道能量以簇为单位，分布比较均匀，更符合中心极限定理的条件，概率密度模型较CM1更趋近于高斯分布。

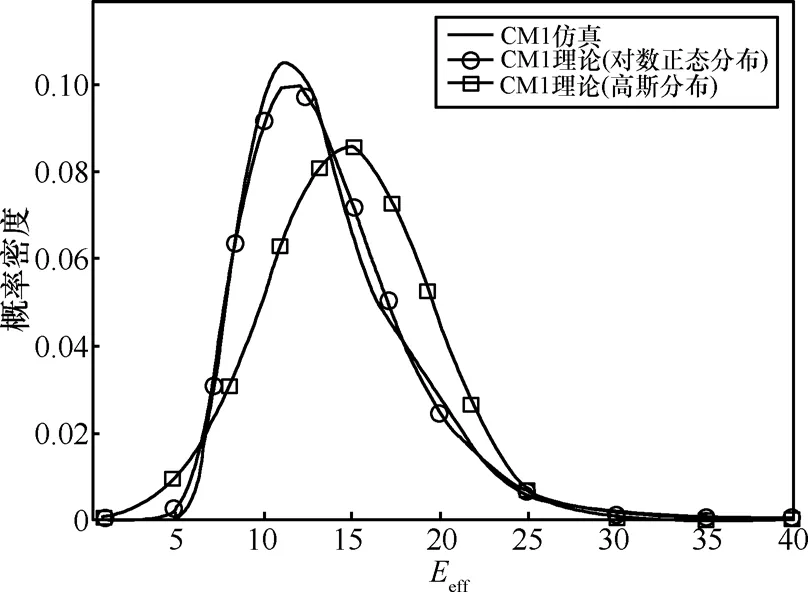
图3 CM1环境下信道能量增益的概率密度逼近

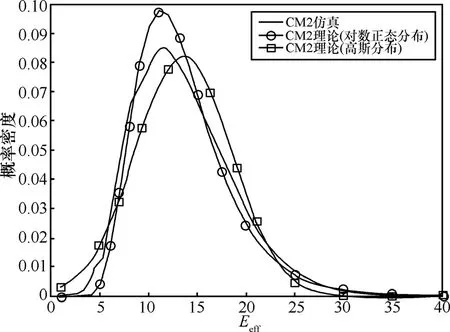
图4 CM2环境下信道能量增益的概率密度逼近

图5和图6分别是CM3和CM4的情况，2种情况均为NLOS情况，信道参数也比较接近。仿真结果介于对数正态分布和高斯分布二者之间。拟合的误差仍然出现在概率密度峰值附近，表1的实验数据表明仿真概率密度的峰度与对数正态分布的差值相对于高斯分布的差值要小一些。尽管 CM3和 CM4情况下多径到达率较大，观察时间内的多径数目远大于前面2种情况，但是，信道的概率密度并没有随着多径数目的增多而更符合中心极限定理，趋近于高斯分布，原因可以解释为尽管多径数量很多，但是对整个信道能量分布影响较大的是簇能量的到达，所以此时信道能量的分布并不趋向于高斯分布。这也证明了文献[17]的结论，信道能量增益的概率密度在一定条件下趋近于高斯分布，但并不收敛于高斯分布。

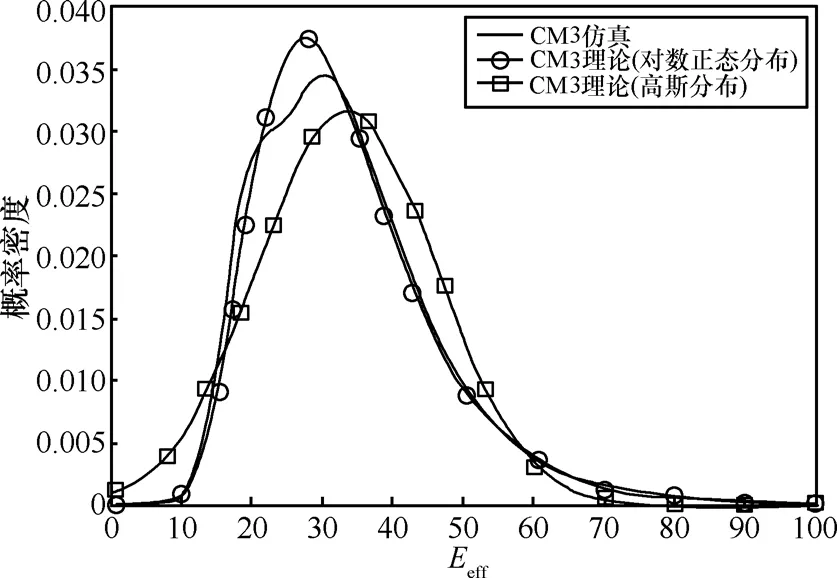
图5 CM3环境下信道能量增益的概率密度逼近

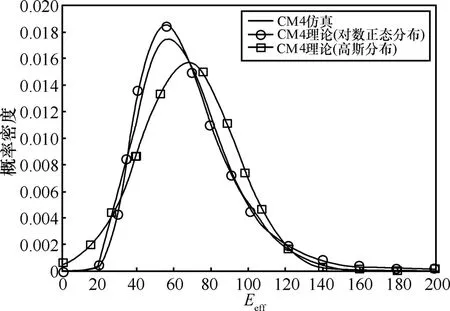
图6 CM4环境下信道能量增益的概率密度逼近

从仿真结果以及以上的分析可以得出结论，利用对数正态分布近似超宽带衰落信道能量概率密度要比高斯分布更具有一定的合理性，而近似带来的误差主要出现在概率密度峰值附近。

2) 超宽带接收机性能仿真验证。

仿真分别对每种信道情况取1 000组信道实现，进行误码率仿真。调制方式分别采用OOK和PPM 2种。噪声条件为加性高斯白噪声，功率谱密度N0/2，信噪比定义为SNR=Eeff/N0，其中，Eeff表示1 000组信道实现下信道能量的均值.

图7～图10分别为CM1～CM4这4组信道情况下接收机的平均误码率曲线。可以看出，CM1、CM3、CM4情况下，基于对数正态分布近似的理论误码率性能与Monte-Carlo仿真结果在OOK调制方式与PPM调制方式下吻合效果较好，在CM2的情况下，2种调制方式下出现一定的偏差，理论性能的曲线要低于仿真曲线。高斯分布的拟合效果较差，在15dB之后，误码率曲线出现平底现象。随着信噪比的增加，逐渐偏离仿真结果。

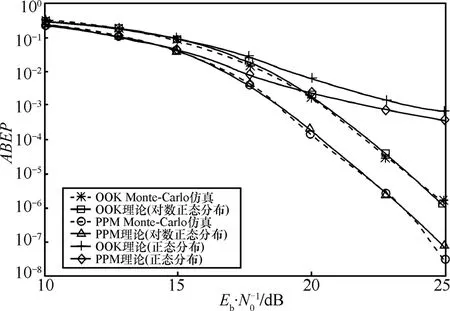
图7 CM1环境接收机误码率曲线

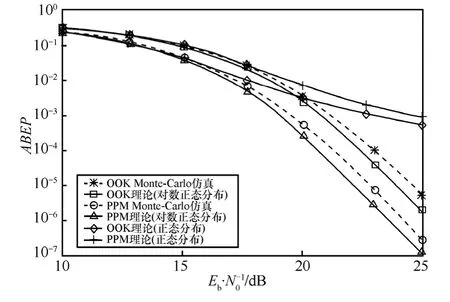
图8 CM2环境接收机误码率曲线

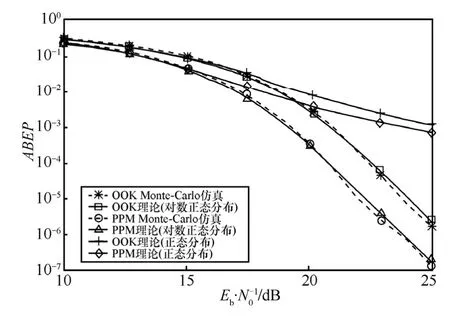
图9 CM3环境接收机误码率曲线

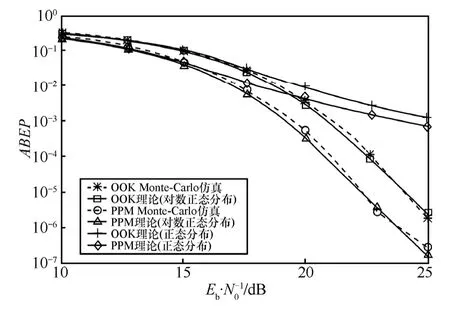
图10 CM4环境接收机误码率曲线

仿真结果表明以下2点。

1) 从评价超宽带接收机的系统性能方面考虑，将信道的能量增益概率密度近似为对数正态分布更有效一些。对于 CM2信道情况，接收机理论性能优于仿真性能，对数正态分布的理论估计可能导致对系统性能的评价偏高。而将信道的能量增益概率密度做高斯分布近似在普遍的信道条件下对系统性能的评估会带来较大的误差。

2) 在不考虑码间干扰以及能量泄露等条件下，采用非相干ED方式接收机时，对比PPM调制方式与OOK调制方式的系统性能。可以看出，接收机平均误码率性能与条件误码率性能曲线得到结果相吻合，当M=100时，PPM相对于OOK方式的误码率性能，从有效信噪比的角度评价，基本趋于常数，与前文定义的2种调制方式的比例因子的结论(当M＞100后，2种调制方式的比例因子趋于常数)相吻合。如图7～图10所示，在M=100条件下PPM调制方式均优于OOK调制方式2dB，且误码率曲线趋于平行。所以选择系统调制制度时需要考虑信噪比情况和接收机窗口长度，另外需要考虑PPM调制占用调制时隙带来的对码速率带来的影响，从而折中设计系统。

5 结束语

为了解决目前非相干超宽带系统在密集多径信道下的平均误码率性能的理论推导问题，本文利用随机点过程理论，对IEEE 802.15.3a的标准信道进行建模，从而避免了工作组给出的信道模型易于仿真而难于理论分析的问题，给出基于OOK和PPM调制方式下的超宽带非相干接收机平均误码率的数学表达式。围绕着该性能指标的数学表达式中多径能量增益的概率密度，推导出能量增益的统计均值和方差的精确解，并通过若干数字特征深入分析了其统计特性，经过与高斯分布和对数正态分布之间的对比分析，确定采用对数正态分布来拟合能量增益的概率密度，并通过Monte-Carlo仿真验证了概率密度拟合的合理性。在此基础上，对推导出的平均误码率指标进行数值和仿真分析，结果在4种信道条件下具有较高的一致性，表明本文利用对数正态分布近似为能量增益的概率密度相比于高斯分布更具有有效性。同时，对PPM和OOK 2种调制制度的性能进行了比较，结果表明当信噪比较低，M=100时，2种调制方式的误码率性能比较接近；随着信噪比的增加，PPM 调制方式下的系统性能优于 OOK调制方式，这种性能的差别随着M的增加而逐渐趋近于常数2dB。但是，由于PPM调制方式需要在时域预留出用于调制的时隙，故相对于OOK调制降低了系统的传输速率，增加了能量开销。

附录A 信道能量增益的方差

首先，将信道能量增益Φ定义为散弹噪声随机变量：

其中，φ(·)表示滤波函数，该函数对二维空间随机点的发生时间t和标值为s进行作用，这里t表示多径到达时间，s表示该径的幅度增益，N为点过程的计数过程。将Φ写成计数积分形式：

其中，N(B)为可测集 B上的计数过程，(ds×du)为 N的可测空间。为求Φ的分布，令 φ(s,t)=s2。

由文献[16]中可得，整个多径信道可划分为4个点过程：N=N00+Nr0+Nc+ N*。故

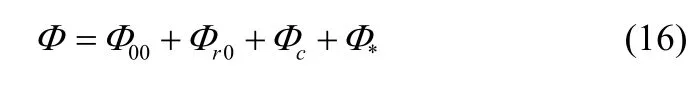
各个参数含义参考文献[16]。因为推导Φ的方差时需要用到其均值，所以对式(16)取期望得

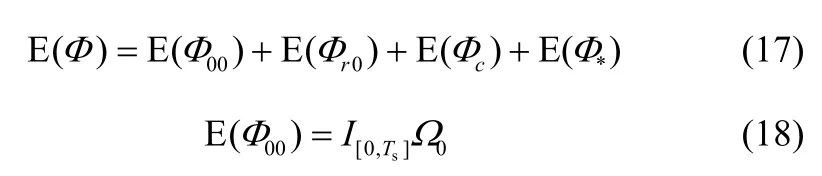
I[0,Ts]为示性函数，Ω0参数定义见文献[13]。根据Campbell定理[20]可得

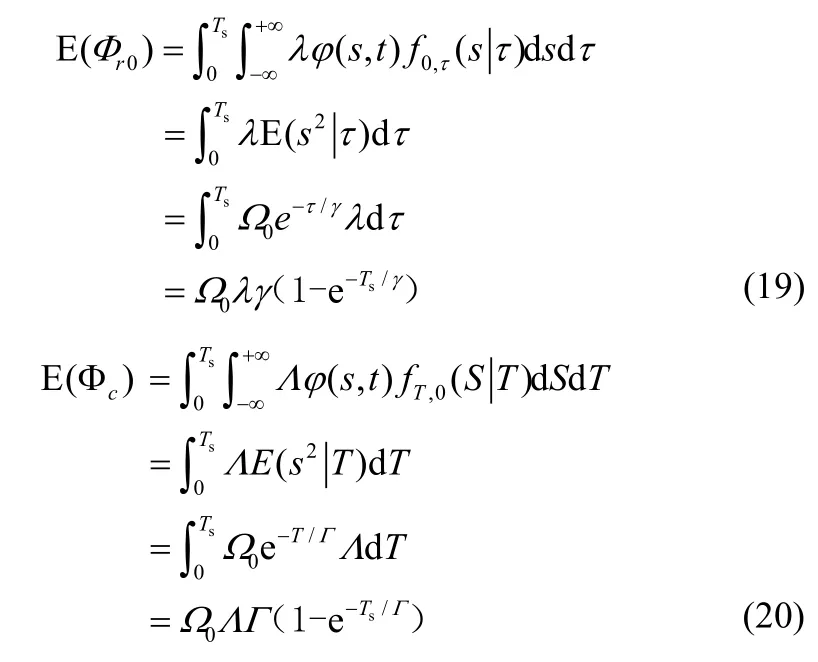
通过对条件期望求均值可得

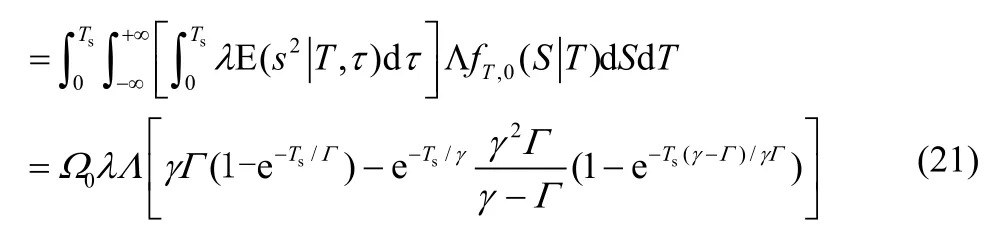
故可得

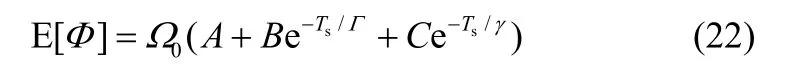
其中，

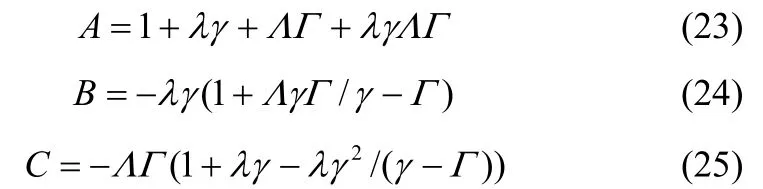
对Ts取极限得

接下来开始推导方差，对式(16)取方差得

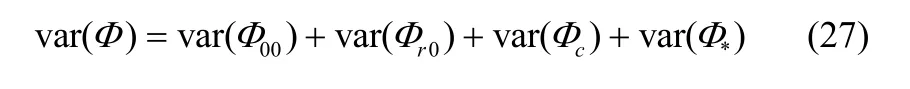
为方便计算，定义常数K

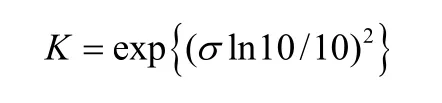
根据对数正态分布性质可得

故

根据Campbell定理

由于随机变量的方差等于条件方差的期望与条件期望的方差之和[20]，故

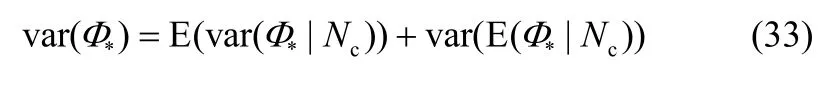
其中，可以求得条件方差为

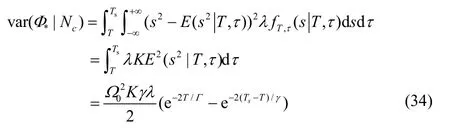
故条件方差的期望为

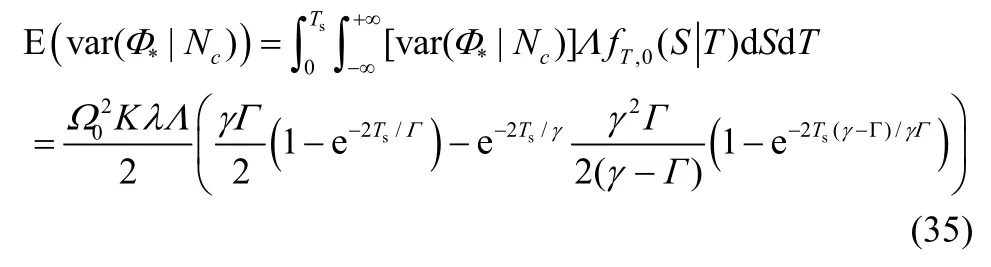
同理，条件期望的方差为

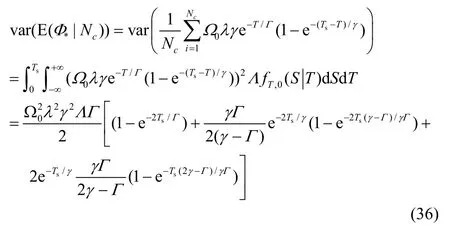
故由式(35)、式(36)相加即可得信号能量的方差，当Ts趋于无穷时，表达式可简化为

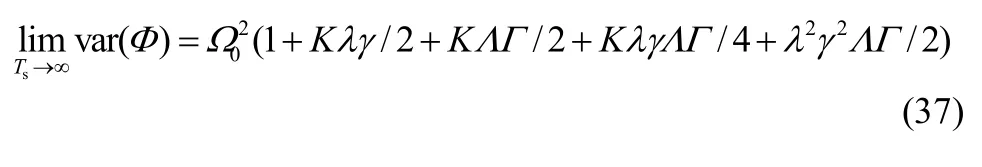
附录B 高斯分布的偏度系数和峰度系数

设随机变量X～N(μ,σ2)，X的矩母函数可以表示为

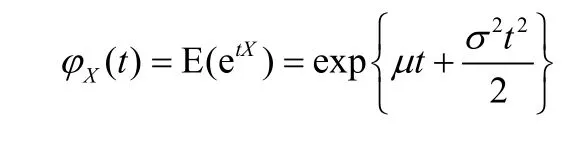
则X的任意阶原点矩

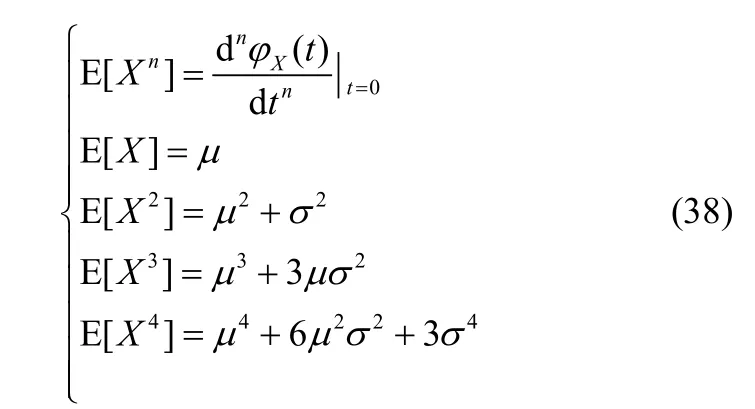
故信号的偏度可以表示为

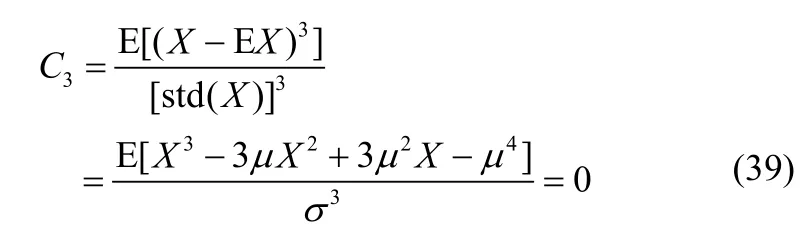
峰度可以表示为

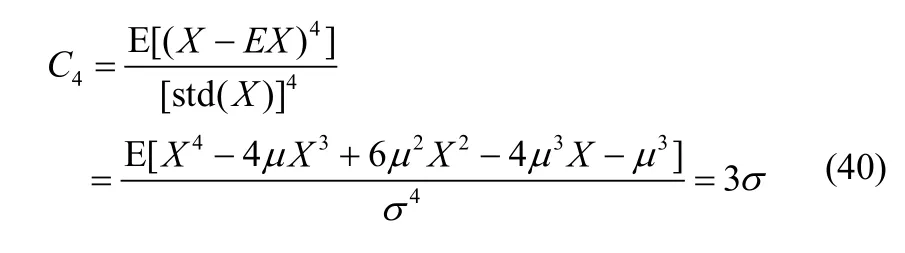
附录C 对数正态分布的偏度系数和峰度系数

设随机变量Y～LN(μ,σ2)，则X的任意阶原点矩

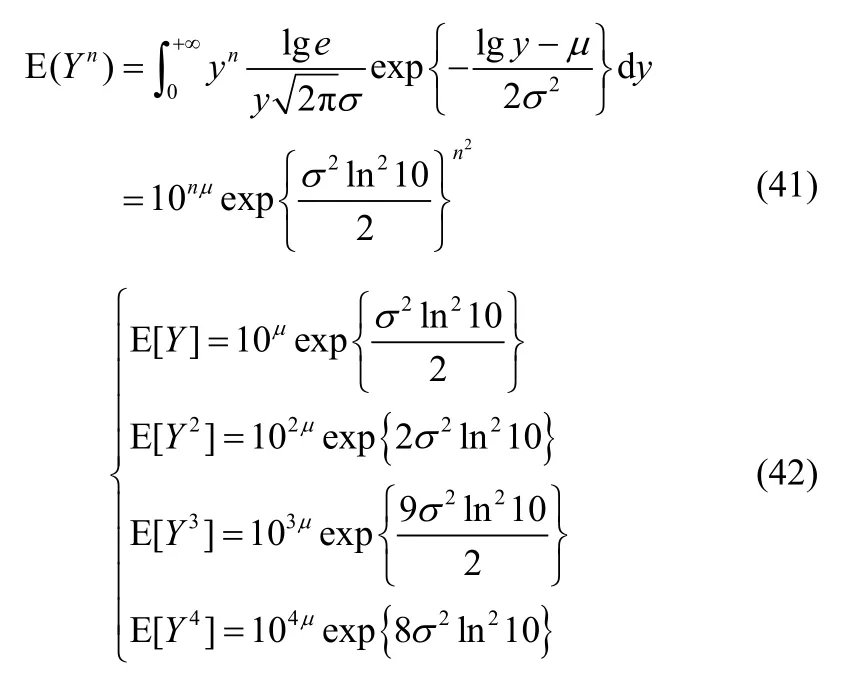
故信号的偏度可以表示为故信号的峰度可以表示为

[1] WIN M Z,SCHOLTZ R A.Impulse radio: how it works[J].IEEE Communications Letters,1998,2(2):36-38.

[2] WIN M Z,SCHOLTZ R A.Characterization of ultra-wide bandwidth wireless indoor channels: a communication-theoretic view[J].IEEE Journal on Selected Areas in Communications,2002,20(9): 1613-1627.

[3] QUEK T Q S,WIN M Z.Analysis of UWB transmitted-reference communication systems in dense multi-path channels[J].IEEE Journal on Selected Areas in Communications,2005.23(9): 1863-1874

[4] TIAN Z,SADLER B M.Weighted energy detection of ultra-wideband signals[A].IEEE 6th Workshop on SPAWC[C].US,New York,2005.1068-1072.

[5] CREPALDI M,CASU M,GRAZIANO M.Energy detection UWB receiver design using a multi-resolution VHDL-AMS description[A].IEEE Workshop on SIPS[C].Greece,Athens,2005.13-18.

[6] SAHIN M E,GUVENC I,ARSLAN H.Optimization of energy detector receivers for UWB systems[A].Proc of IEEE VTC2005-Spring[C].Sweden,Stockholm,2005,2(6):1386-1390.

[7] RABBACHIN A,OPPERMANN I.Synchronization analysis for UWB systems with a low-complexity energy collection receiver[A].International Workshop on UWB(IWUWBS) Joint with Conference on UWB Systems and Technologies(UWBST)-(Joint UWBST &IWUWBS'04)[C].Japan,2004.288- 292.

[8] DIRENZO M,GRAZIOSI F,SANTUCCI F.An exact framework for performance analysis of IR-UWB systems: the need for approximations[J].IEEE Communications Letters,2007,11(10):769-771.

[9] TIAN Z,SADLER B M.Weighted energy detection of ultra-wideband signals[A].Proceedings of IEEE 6th Workshop on Signal Processing Advances in Wireless Communications[C].New York USA,2005.158-162.

[10] PENG X,CHIN F,WONG S H,et al.A rake combining scheme for an energy detection based noncoherent OOK receiver in UWB impulse radio systems[A].IEEE ICUWB 06[C].2006.73-78.

[11] KIM J,KIM S,SUNG W,et al.Selective signal combining for effective BER improvement in non-coherent IR-UWB systems[J].IEICE Transactions,2008,91-A(11): 3197-3200.

[12] SAHIN M E,GUVENC I˙S.Joint parameter estimation for UWB energy detectors using OOK[J].J of Wireless Personal Communications,2007,40: 579-591.

[13] FOERSTER J.Channel Modeling Sub-Committee Final Report[R].IEEE,P802.15-20/368r5-SG3a,2002.

[14] MARVIN K S,MOHAMED S A.Digital Communication over Fading Channels.Second Edition[M].Wiley IEEE Press,2004.5-14.

[15] HUMBLET P A,AZIZOGLU M.On the bit error rate of lightwave systems with optical amplifiers[J].Lightwave Technology,1991,9(11):1576-1582.

[16] GUBNER J A,KEI H.A computable formula for the average bit error probability as a function of window size for the IEEE 802.15.3a UWB channel model[J].IEEE Transactions on Microwave Theory and Techniques,2006,54(4):1762-1768.

[17] 王定成,胡苏.对数正态型分布纪录值之和的渐近分布[J].中国科学: A辑,2002,32(7):603-612.WANG D C,HU S.The asymptotic distributions of sums of record values for lognormal distributions[J].Sci China Ser A,2002,32(7):603-612.

[18] LIU H.Error performance of a pulse amplitude and position modulated ultra-wideband system over lognormal fading channels[J].IEEE Communications Letters,2003.7(11):531- 533.

[19] BEAULIEU N C,ABU-DAYYA A A,MCLANE P J.Estimating the distribution of a sum of independent lognormal random variables[J].IEEE Transactions on Communications,1995,43(12): 2869.

[20] PARZEN E.Stochastic Processes[M].Third Edition,San Francisco,CA: Holden-Day,196.149-151.