译码转发中继系统基于校验分裂的IRA 码设计

孙小钧，姜明，赵春明，吴晓富,2

(1.东南大学 移动通信国家重点实验室，江苏 南京 210096; 2解放军理工大学 通信工程学院，江苏 南京 210007 )

1 引言

近年来，无线中继技术领域成为人们研究的热点。在协同中继系统中，一个传输时隙被分为2个阶段。在第一个传输阶段，即广播阶段，源节点首先广播信号。在第二个传输阶段，即中继阶段，中继节点对接收信号或者进行放大转发(AF)，或者进行译码转发(DF)给终端[1]。虽然DF方式的复杂度较 AF方式高，但在低信噪比时性能较优异[1]。基于低密度校验码(LDPC)的DF中继通信系统已经被广泛研究，码率兼容LDPC码可以通过凿孔或者扩展来得到[2～7]。由于码字的不同部分的信噪比不同，修正的密度进化(density evolution)算法在文献[4,6,7]中被提出。本文考虑了半双工中继通信系统并且在中继阶段，中继节点和源节点都发送相同的信息[3,6,7]。

非规则重复累积(IRA)码是 LDPC码和 Turbo码共有的一个特殊子类，IRA码能够用Tanner图表示，通过节点度的分布来确定码结构，可以应用和积译码算法迭代译码。LDPC码的各种译码算法已被广泛研究[8～12]。与LDPC码相比，IRA码的译码性能同样逼近香农限，并且具有线性时间的编码复杂度，便于硬件实现；与Turbo码相比，优化的IRA码的误码平层比较低[13～16]。逼近香农限的码率兼容IRA码可以通过凿孔来获得从低码率到高码率一系列码字[14]，也能通过校验分裂(check-splitting)构造从高码率到低码率一系列码字[15]。与上述DF中继系统采用的码率兼容LDPC码不同，本文将校验分裂技术引入了DF中继系统，并对得到的码率兼容IRA码 C=[C1,Ce]和子码C1进行优化。

在译码转发半双工中继系统中，IRA码的设计本质上是设计一个码率兼容IRA码，并且码字的不同部分经历不同的信噪比，这与传统的码率兼容IRA码不同。对于译码转发中继系统来说，中继节点首先对接收的比特C1进行译码，如果成功译码，中继节点产生新的校验比特Ce传给终端节点；终端节点将新的校验比特与在广播阶段接收的比特形成一个低码率码字C。这个低码率码字C通过对高码率码字C1进行校验分裂来得到。考虑到信噪比在一个通过校验分裂得到的码字内是不同的，本文给出了修正的高斯近似的密度进化算法，如EXIT图[16]，来分析校验分裂IRA码的门限。本文利用差分进化(differential evolution)算法来同时优化这2个码字C和C1。与传统的密度进化算法设计的码率兼容IRA码相比，基于校验分裂的修正的密度进化算法优化得到的码字有0.5dB的增益。

2 半双工DF中继系统模型

本节主要简单介绍时分半双工DF中继通信系统模型及其信道容量[3]。如图1所示，3节点(源节点S，中继节点R与终端节点D)时分半双工中继通信系统需要2个时隙t和t′=1-t来实现。本文假设每一个节点都只有一个天线。

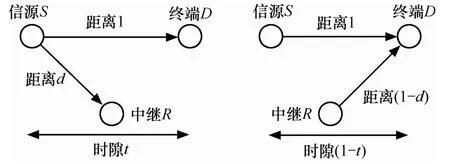
图1 中继系统模型

在广播阶段，源节点向中继节点与终端节点广播信号x1；在中继阶段，终端节点同时接收来自源节点与中继节点的信息，表示为x2，假设终端节点没有同步误差的问题。{S,D}的距离设为1，{S,R}的距离表示为d，{R,D}的距离表示为1-d；相应的路径损耗分别是，α表示信道衰减指数，文中设定α=2。D和R在广播阶段接收的信号分别为

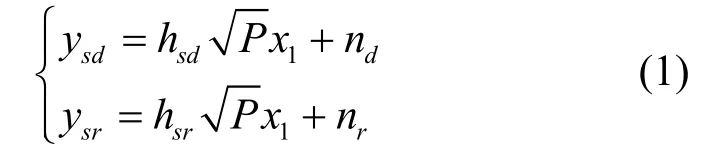
D在中继阶段接收的信号为

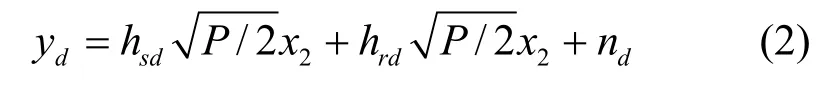
其中，P表示S在广播阶段的发射功率；为了保证广播阶段和中继阶段的发射功率相同，本文采用了简单的平均功率分配方案，即S和R在中继阶段的发射功率是S在广播阶段的发射功率的一半；nr和nd是加性高斯白噪声，均值为零，方差N0，即 N(0,σ2)。

文献[3]给出的DF中继系统的信道容量表达式为

其中， I(x ; y)表示为x与y的互信息。当RDF确定时，信道容量界(CB,capacity bound)是指满足式(3)所需的最低信噪比。

3 DF中继系统基于校验分裂的递增冗余IRA码设计

本节首先简要介绍IRA码[13,14]及其高斯近似的密度进化算法[16]。为了得到码率兼容递增冗余IRA码，校验分裂技术[15,17]被引入。由于码字的不同部分经历的信噪比不同，适用于DF中继系统的基于校验分裂的高斯近似的密度进化算法在本节中被提出并用来分析IRA码的门限。最后，差分进化算法被用来同时寻找性能优良的IRA码C和子码C1。

3.1 IRA码简介

如图 2所示，参数是（f3,…, fJ;a） 的 IRA码Tanner图，有k个信息节点，m个校验节点和m个奇偶节点。 fi＞ 0表示与校验节点相连的有i条边的信息节点占总信息节点的百分比，且满足为了实现任意低的码字错误概率，信息节点的度i必需满足i＞2[14]。a,b是与校验节点相连的信息节点数，除了第一个奇偶节点的度是 1外，其余每个奇偶节点的度是2。本文只讨论系统IRA码，奇偶节点位于校验矩阵的右半部分，排列成双对角形式。

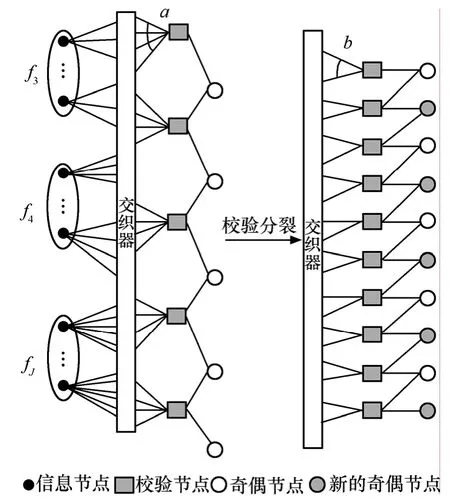
图2 IRA码的Tanner图及Check-Splitting的Tanner图

函数J(μ)由文献[16]给出。在差分优化算法中，式(4)被用于分析子码的门限xa。当迭代次数达到最大值lmax后，结束进化并记录 xa=xlmax。

3.2 校验分裂简介

文献[15,17]提出了对已有码字的校验节点进行分裂来得到新的码率兼容码字，即校验分裂，如图2所示。基本上，一个校验节点连接a个信息节点，2个奇偶节点。所谓校验分裂，即一个校验节点分裂成 2个校验节点(每个校验节点连接b=a/2个信息节点)，分别与1个新的奇偶节点相连。高码率子码C1码经过校验分裂后，产生m个新的奇偶节点，从而得到了低码率的母码C，码率是并且信息节点的分布函数λ(x)保持不变，新的校验矩阵仍然保持双对角特性。由于 IRA码的上述特性，大大简化了联合优化子码C1和母码C的计算量。

3.3 基于校验分裂的DF中继IRA码的密度进化算法

在基于校验分裂的半双工DF中继系统中，码率兼容递增冗余IRA码 C=[C1,Ce]由2部分构成，高码率的子码C1和校验分量Ce。子码C1在广播阶段被S发射出去，假设R译码成功，则在中继阶段，S和R发射校验分量Ce。R接收的子码C1经历的信噪比是。而D接收码字的不同部分经历的信噪比是不同的，即子码C1经历的信噪比是，而校验分量Ce经历的信噪比是。而传统的码率兼容 IRA码的不同部分经历的信噪比是一样的。DF中继系统码率兼容IRA码的设计实际上是联合设计子码C1和C，使得子码C1接近{S,R}信道容量，而C逼近DF中继系统的信道容量。

由于子码C1和校验分量Ce经历的信噪比不同，而式(4)描述的密度进化算法假设码字经历的信噪比是相同的，所以本小节推导了适用于DF中继的校验分裂的IRA码密度进化算法。由文献[16]的译码信息更新机制，令ui表示信息节点的初始信息对数似然比，ur,p和us,p表示新的和旧的奇偶节点的初始信息对数似然比。第l次迭代时，令表示从校验节点输出到新的和旧的奇偶节点的外信息，表示从校验节点输出到与之相连的第k个信息节点的外信息；类似地，表示新的，旧的奇偶节点和第k个信息节点输出到校验节点的外信息。译码过程中，各个节点的信息更新机制为

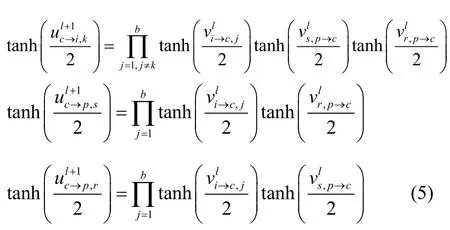
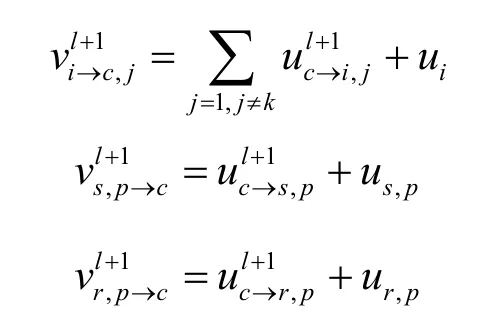
设C1经历的AWGN信道分布服从，Ce经历的 AWGN信道分布服从。令μ=2/σ2，μ=2/σ2。令 P表示第l次迭代时，信息节点传输给校验节点的外信息概率分布密度；Ql表示第l次迭代时，校验节点传输给信息节点的外信息概率分布密度；表示第l次迭代时，旧（新）奇偶节点传输给校验节点的外信息概率分布密度；)表示第l次迭代时，校验节点传输给旧（新）奇偶节点的外信息概率分布密度； Γ(Γ-1)表示概率密度函数映射(逆映射)。假设Tanner图无圈，由式(5)及概率密度卷积性质，可得密度进化迭代关系式：其中，Fo表示子码C1经历的信道初始消息分布的概率密度，Fn表示校验分量Ce经历的信道初始消息分布的概率密度，⊗表示卷积，⊗m表示m重卷积，基于EXIT图的高斯近似密度进化算法满足如下递推公式：

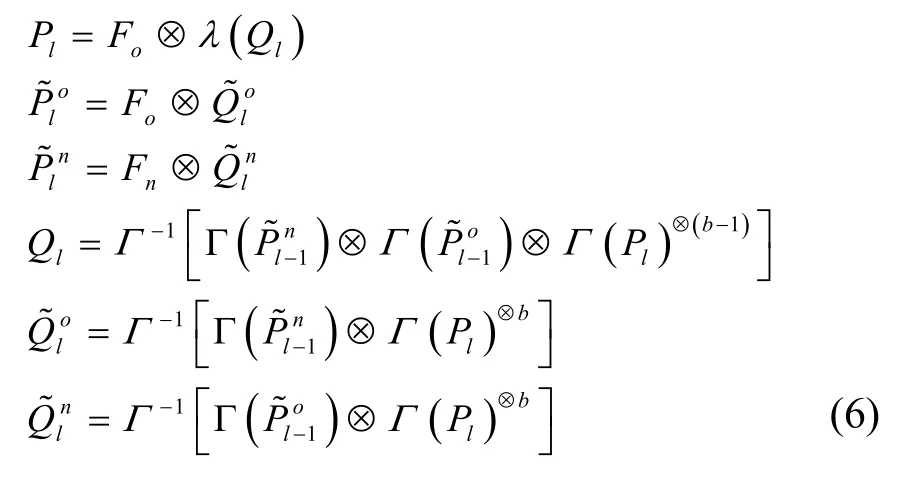
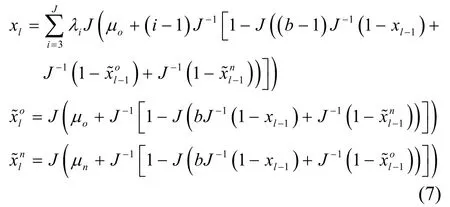
在差分优化算法中，式(7)被用于分析子码的门限xb。当迭代次数达到最大值lmax后，结束进化并记录 xb=xlmax。高斯近似算法计算速度快，精度损失在可以接受的范围内，因而被广泛运用。

3.4 DF中继IRA码的优化

差分进化算法作为一种简单有效的优化算法已经被广泛应用来搜索码的最优分布[6,18]。本小节用差分进化算法来同时优化C和高码率的子码C1。在优化IRA码的分布{λi, a}之前，首先要去掉参数之间的相关性[18]。由于λ3、λdv可以由其他参数确定，则优化参数表示成一个L维向量 q=(λ4,…,λdv-1,a)。差分进化算法的流程如图3所示，具体的优化步骤如下。

图3 差分优化算法的流程图

1) 初始化：令G表示差分进化的次数。对于初始进化G=0，随机产生NP=10L个进化向量qg,G(g=1,…,NP)。对于每个向量qg,G计算式(4)和式(7)，直到达到预设最大迭代次数（如1 000次），记录 xg,G=min(xa,xb)，从中选出最大值xbest,G对应的向量，记为qbest,G。

2) 交叉：在qg,G的基础上产生新的进化向量qg,G+1。随机选择4个不同的向量qr1,G，qr2,G，qr3,G和qr4,G，F是控制交叉变异的实常数，一般赋值F=0.5，则新的向量按照式(8)计算

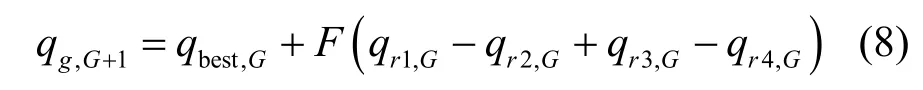
对于 qg,G+1，迭代计算式(4)和式(7)，然后记录xg,G+1=min(xa,xb)。

则 qg,G+1=qg,G，xg,G+1=xg,G。从xg,G+1中选出最大值 xbest,G+1对应的向量，记为 qbest,G+1。

4) 停止判断：如果 xbest,G+1小于预定值并且差分进化次数没有达到最大次数(条件1)，则返回步骤2；如果xg,G+1大于预定值或差分进化次数达到最大次数(条件2)，则在调整后，返回步骤1。当xg,G+1大于预定值时，其对应的分布 qbest,G+1被称为最佳分布如果调整前后的差值比较小(如10-4，条件3)，则停止进化，输出最佳分布。

4 仿真结果

为了与基于传统密度进化算法得到码字相比较，传统递增冗余IRA码的分布是[14]称之为高斯IRA码。

分布(λDF,a=6)和(λGS,a=8)对应高码率的子码C1，而分布(λDF,b=3)和(λGS,b=4)对应低码率的IRA码C。为了得到递增冗余的2个校验矩阵，首先用 PEG算法构造出高码率子码C1的校验矩阵H1=[Ξ Π]（Ξ 代表信息节点子矩阵，Π 代表奇偶节点子矩阵并且是双对角结构），然后将Ξ子矩阵的每行分裂成2行，即将Ξ每行a个信息节点的一半(b个)信息节点组成新矩阵 H的信息节点子矩阵的一行。这样得到的低码率母码C的校验矩阵H未必是最佳矩阵，但仿真表明其译码性能仍然比较优秀。下一步将研究如何构造好的分裂校验矩阵H。

具有强大纠错能力的Turbo码也被DF中继系统广泛应用[19]，本节也比较了分布式 Turbo码和DF-IRA码的性能。仿真的分布式Turbo码的分量码是生成矩阵为(1 3,15 )8的递归系统卷积码，广播阶段使用了0.5码率的Turbo码，如果中继节点译码成功，D在中继阶段接收新的校验比特，最后分布式Turbo码的码率是1/3。

为了合理比较采用不同码字的DF中继系统的性能，首先分析了DF-IRA码，高斯IRA码和分布式Turbo码的译码复杂度。IRA码的最大译码迭代次数为100，Turbo码的迭代次数为14。对于1/3码率的 DF-IRA码，每个信息比特每次译码需要(2 b+3)×2+2+ 4次加法，需要(b+2)×4次查表，即总共需要54次运算，而1/3码率的高斯IRA码总共需要66次运算[14]。可以看出DF-IRA码的运算量大约是高斯IRA码的82%。对于Turbo码，每个信息比特每次Log-MAP译码大约需要205次运算。即DF-IRA码的最大运算量与Turbo码的最大运算量基本相同，但在并行译码方面，IRA码有明显优势，而停止准则进一步降低了译码复杂度。

图4比较了DF-IRA码，高斯IRA码和分布式Turbo码的误帧率。仿真时，信息长8 192bit。本文假设高斯IRA码在R节点总能成功译码，而DF-IRA码和分布式Turbo码在R节点译码失败时，R节点转发信息位。从图4中可以看出，针对DF中继系统优化得到的 DF-IRA码的性能优于传统的 IRA码，当误帧率是 2×10-3时，与高斯 IRA码相比，DF-IRA码大约有 0.5dB的增益。当误帧率是 10-1时，与 DF-IRA码相比，分布式 Turbo码大约有0.15dB的增益；但当误帧率是 10-3时，分布式Turbo码已经出现了误码平层，而DF-IRA码没有出现误码平层。当误帧率是 2×10-3时，本文得到的IRA码与DF中继信道容量对应的CB界 CB=-5 dB 相比，大约有1.1dB的差距。进一步的工作将是寻找能够更好的逼近CB界的DF-IR A码的分布。

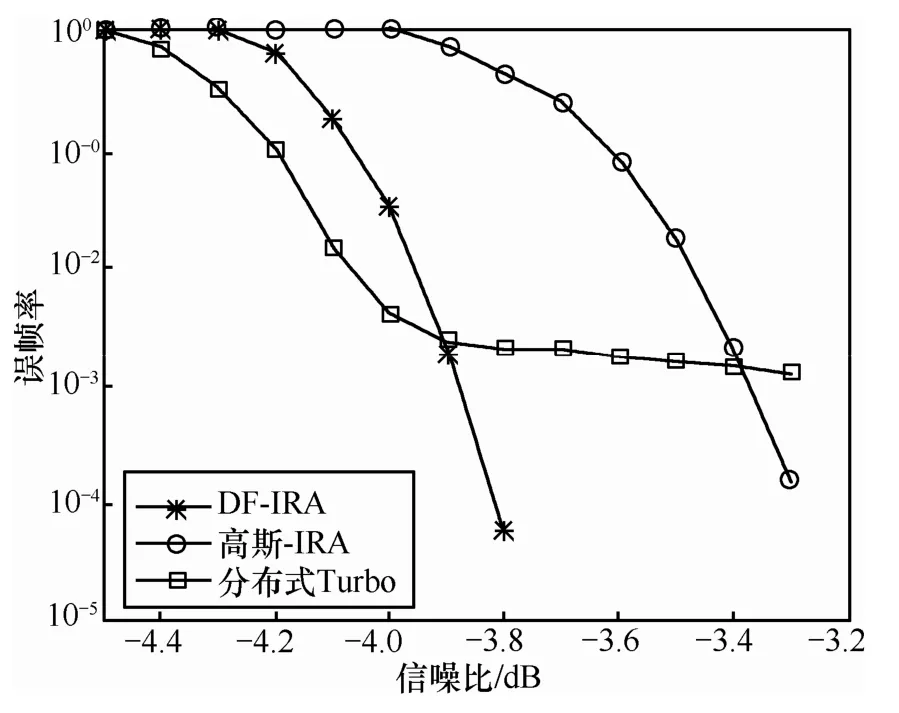
图4 DF-IRA码、高斯IRA码和分布式Turbo码的误帧率

5 结束语

DF中继系统 IRA码的设计实际是寻找一个递增冗余码字，使其在中继系统中性能优良的同时子码在{S,R}信道中性能仍然优良。递增冗余 IRA码可以通过对子码使用校验分裂技术来实现。针对译码转发中继系统的特点，即非规则重复累积码(IRA)的不同部分经历不同的信噪比，本文给出了基于校验分裂的修正的高斯近似的密度进化算法，并且用差分进化算法来同时搜索母码和子码好的分布。当误帧率是 10-3时，与传统的密度进化算法得到的IRA码相比，本文优化得到的码字大约有0.5dB的增益。

[1] LANEMAN J N,WORNELL G W.Distributed space-time-coded protocols for exploiting cooperative diversity in wireless networks[J].IEEE Trans Inform Theory,2003,49(10):2415-2425.

[2] JUN H,TOLGA M D.Low density parity check codes over wireless relay channels[J].IEEE Trans Wireless Commun,2007,6(9):3384-3394.

[3] ARNAB C,et al.Low density parity check codes for the relay channel[J].IEEE Journal Selec Commun,2007,25(2): 280-291.

[4] PEYMAN R ,WEI Y.Bilayer low-density parity-check codes for decode-and-forward in relay channels[J].IEEE Trans Inform Theory,2007,53(10):3723-3739.

[5] KIM J,et al.Joint LDPC codes for multi-user relay channel[A].Proc IEEE NCTA[C].2008.1-6.

[6] CHUXIANG l,et al.LDPC code design for half-duplex cooperative relay[J].IEEE Trans Wireless Commun,2008,7(11): 4558-4566.

[7] JEAN P C,VAHID M.Optimized low density parity-check codes designs for half-duplex relay channels[J].IEEE Trans Wireless Commun,2009,8(7): 3390-3395.

[8] 贾科军,柯熙政,彭铎等.大气激光通信系统中π-旋转LDPC码的设计与性能分析[J].兰州理工大学学报,2008,34(4):109-113.JIA K J,KE X Z,PENG D,et al.Design of π-rotation LDPC for atmospheric laser communication system and its performance analysis[J].Journal of Lanzhou University of Technology,2008,34(4): 109-113.

[9] 杨晔,张志平,廖伟.基于调度的高效 LDPC译码算法[J].武汉理工大学学报,2009,31(18):46-50.YANG Y,ZHANG Z P,LIAO W.Scheduling-based efficient LDPC decoding algorithm[J].Journal of Wuhan University of Technology,2009,31(18):46-50.

[10] 胡新桂,孙刚.一种LDPC码校验矩阵消短环算法[J].计算机工程与科学,2009,31(9):156-158.HU X G,SUN G.An algorithm of the short cycle in check matrix of LDPC be eliminated[J].Computer Engineering & Science,2009,31(9):156-158.

[11] 乔华,管武,董明科等.LDPC码高速译码器的设计与实现[J].北京大学学报,2008,44(3):347-352.QIAO H,GUAN W,DONG M K,et al.Design and implementation of LDPC decoder with high throughput[J].Acta Scientiarum Naturalium Universitatis Pekinensis,2008,44(3):347-352.

[12] 姜明.低密度奇偶校验码译码算法及其应用研究[D].南京: 东南大学,2006.JIANG M.Research on the Decoding Algorithms of Low-density Parity-Check Codes and Their Applications[D].Nanjing: Southeast University,2006.

[13] 雷菁,徐富兵,唐朝京.IRA 码密度进化方法分析与门限判决[J].通信学报,2007,28(10):67-72.LEI J,XU F B,TANG C J.Analysis on density evolution method and threshold decision for IRA codes[J].Journal on Communications,2007,28(10):67-72.

[14] WU X,et al.Design of rate compatible punctured IRA codes for IR-HARQ schemes[J].Journal of Southeast University,2008,24(2):127-132.

[15] HAOMING L,MARSLAND I D.A comparison of rateless codes at short block lengths[A].Proc IEEE ICC[C].2008.4483-4488.

[16] ALINE R,et al.Design methods for irregular repeat-accumulate codes[J].IEEE Trans Inform Theory,2004,50(8):1711-1727.

[17] SHI C,RAMAMOORTHY A.Design and analysis of E2RC codes[J].IEEE Journal on Selected Areas in Communications,2009,27(6):889-898.

[18] JILEI H,et al.Performance analysis and code optimization of low density parity check codes on Rayleigh fading channels[J].IEEE Journal Selec Commun,2001,19(5): 924-934.

[19] ZHENG Z,TOLGA M D.Capacity-approaching Turbo coding for half-duplex relaying[J].IEEE Trans Commun,2007,55(10): 1895-1906.