闪锌矿型HgTe电子结构和光学性质的第一性原理计算

刘其军 刘正堂 冯丽萍

(西北工业大学材料学院,西安 710072)

在Ⅱ-Ⅵ族半导体材料中,HgTe由于具有半金属特性而倍受关注[1-3].HgTe及其相关的半导体材料被广泛应用于红外量子阱探测器、MIS红外器件、自旋场效应晶体管、太阳能电池和光电器件等领域[4-9].因此,对HgTe进行了广泛而深入的研究[10-16].王新强等[13-15]采用基于密度泛函理论框架下的第一性原理方法,计算了(HgTe)n团簇的基态结构、能隙和结合能;Lu等[17]和Hao等[18]分别采用线性缀加平面波方法(LAPW)和局域密度近似平面波超软赝势法计算了在不同压力下HgTe的结构性质.然而结合能带结构和态密度对闪锌矿型HgTe光学性质进行分析的报道很少,而这些微观机理对于深入了解闪锌矿型HgTe宏观的光学特性是十分必要的.同时,采用第一性原理平面波超软赝势法已成功地计算了金属[19]及半导体材料[20].因此,采用基于密度泛函理论(DFT)的平面波超软赝势法计算了闪锌矿型HgTe的电子结构和光学特性,并从理论上分析了它们之间的关系,为实验研究及实际应用提供了理论支持.

1 计算方法和模型

采用 Accelrys公司的 Materials Studio中的CASTEP模块进行计算.此模块基于密度泛函方法的从头算量子力学程序:利用平面波赝势方法,将离子势用赝势替代,电子波函数用平面波基矢组展开,电子-电子相互作用的交换和相关势由局域密度近似(LDA)或广义梯度近似(GGA)进行校正,它是目前较为准确的电子结构计算的理论方法[21].本文计算的交换关联能采用广义梯度近似(GGA)中的PW91,计算中平面波截断能Ecut取为210 eV.自洽场运算中,自洽精度设为每个原子能量收敛至5.0×10-6eV,作用在每个原子上的力不超过0.1eV/nm,内应力不大于0.02 GPa.在模型的结构优化中,采用了BFGS算法,布里渊区积分采用Monkhorst-Pack的4×4×4进行分格.在用超软赝势描述价电子与芯态关系时,Hg的结构为[Xe]4f145d106s2,价电子取5d10和6s2,Te的结构为[Kr]4d105s25p4,价电子取5s2和5p4.闪锌矿型HgTe晶体结构的空间群为F-43m,晶胞中原子坐标为:Hg:(0,0,0);Te:(0.25,0.25,0.25).

2 计算结果及讨论

2.1 几何结构优化

经过优化计算,获得了闪锌矿型HgTe基态晶格结构,使得整个体系的总能量最小,优化后得到的晶格参数列于表1,同时与其他理论计算值及实验值进行了对比.通过比较可以看出,理论计算值与实验值都能很好吻合,说明计算结果是可信的.

表1 优化后闪锌矿型HgTe的晶格参数与计算值[2,11,17-18]及实验值[12,22]比较

2.2 电子结构

在几何结构优化后,闪锌矿型HgTe沿布里渊区高对称点方向的能带结构计算结果如图1所示.由图1可以看出,闪锌矿型HgTe的最小带隙为0eV,说明了闪锌矿型HgTe的半金属性,同时与文献[2]的计算结果-1.05eV(GGA)和-1.13eV(LSDA),文献[11]的计算结果-0.84eV相比,更接近于实验值-0.14eV[22](0～0.3eV[23]).此外,计算得到G→X,G→R,G→M的值分别为:1.91 eV,0.80 eV,2.08 eV.

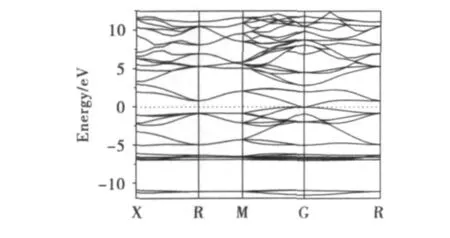
图1 闪锌矿型HgTe的能带结构图

图2给出了闪锌矿型HgTe总态密度和分态密度图.从图2可以看出,在-12.24eV～-9.89eV范围内,主要由Te的5s电子构成,其中态密度的峰值出现在-10.90eV处;在-7.75eV～-5.39eV范围内,主要由Hg的5d电子构成,同时杂化了Te的5p电子,其中态密度峰值出现在-6.55eV处;在-5.39 eV～-3.13eV范围内,主要由Hg的6s电子构成,同时杂化了Te的5p电子,其中态密度峰值出现在-4.68eV处;在费米能级附近的价带,主要由Te的5p电子构成,同时杂化了Hg的5p电子,其中态密度曲线分别在-1.65eV和-1.13eV处出现峰值.

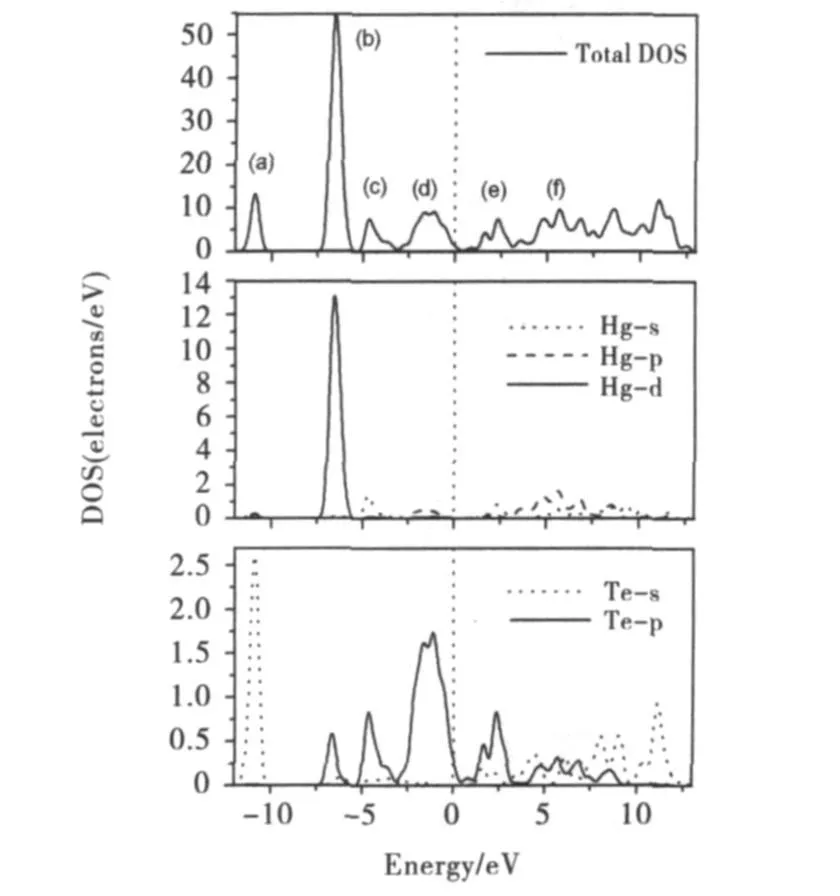
图2 闪锌矿型HgTe的总态密度和分态密度图

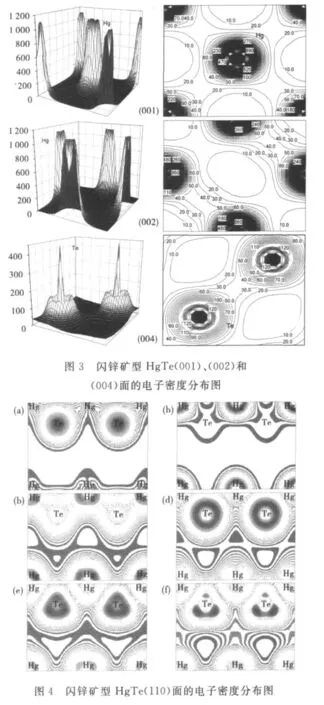
闪锌矿型 HgTe(001)、(002)、(004)面的电子密度图如图3所示.由于电子密度分布能够表征原子键合的情况,Kuroiwa[24]认为当成键的两个原子间最低电子密度与背景电子密度相等时,原子间主要是离子键作用;当两个原子间最低电子密度高于背景电子密度时,主要是共价键作用.因此,从图3可以看到,Te-Te和面心位置的Hg-Hg之间具有共价性.同时,为了弄清Hg-Te之间的成键关系,结合态密度图(图2)中各能量范围内的电子贡献,作出了(110)面各能量范围内的电子密度图,如图4所示,图4(a)、(b)、(c)、(d)、(e)和(f)分别与总态密度图中的各相应区域相对应.从图4可以看出,各电子密度图如实反映了态密度图中各轨道电子的贡献,同时可以看出,Hg-Te之间形成了共价键,主要的成键电子是Hg的6s、5p电子和Te的5p电子.

2.3 光学性质

利用第一性原理赝势平面波法计算了闪锌矿型HgTe的光学性质,考虑到计算方法本身得到的带隙值0eV比实验值小(0～0.3eV[23]),利用剪刀算符进行修正,引入的修正因子为0.15eV将带隙提高到实验平均值0.15eV(因为在计算能带结构时,由于计算方法本身在求解Kohn-Sham方程时没有考虑体系的激发态,使得价带及其以上的能级位置偏低,而价带及以下能级与实验一致,这虽然不影响计算结果对能带结构和电子结构的分析[25],但是在对光学性质进行分析时,需要进行带隙修正,因此引入修正因子将计算得到的带隙值提高到实验值).计算得到闪锌矿型HgTe的复介电常数和复折射率曲线如图5～6所示.从图中可以看到,ε1(0)=19.24,并在 0.77eV 处达到最大值41.66;n(0)=4.39,此结果大于实验值3.7[12,22],并在0.80eV处达到最大值6.68.

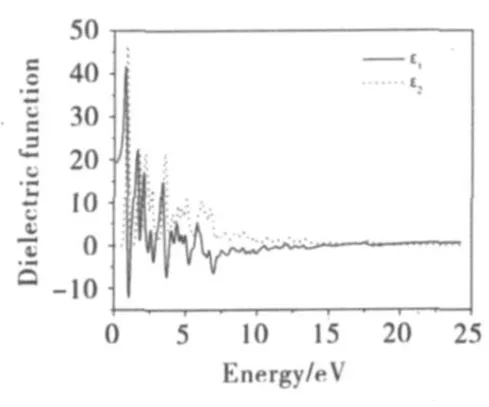
图5 闪锌矿型HgTe的复介电常数

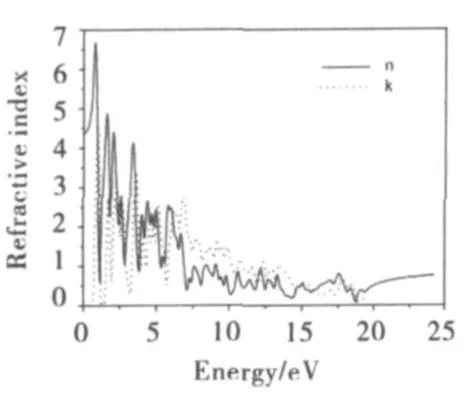
图6 闪锌矿型HgTe的复折射率

计算得到闪锌矿型HgTe的反射率、吸收系数、损失函数和光电导率如图7所示.反射峰是固体电子在光电磁波场微扰作用下发生带间跃迁的宏观表现.随着光子能量的增加,反射率在增加,并在1.08 eV处达到第一次极大值,为0.680,随后反射率减小,之后又不断变化,并在 7.05 eV处达到最大值,为0.759,之后在18.75eV处达到极大值0.751.吸收系数表示光波在介质中单位传播距离光强度衰减的百分比.

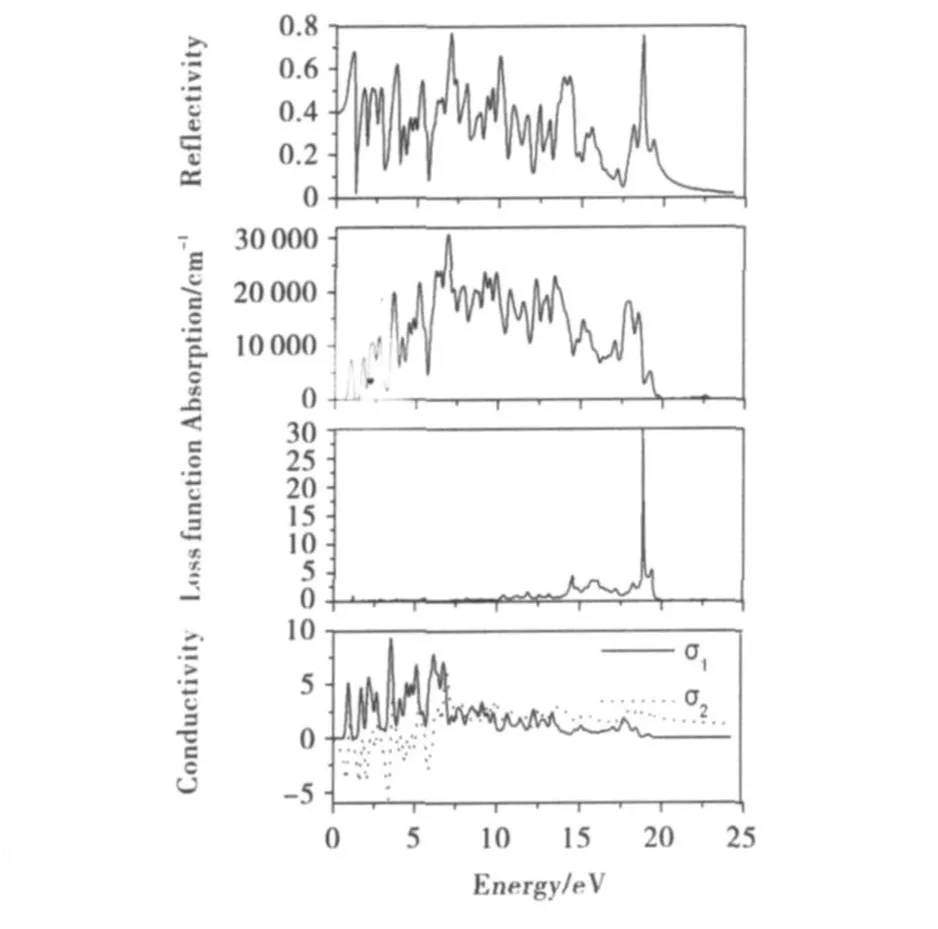
图7 闪锌矿型HgTe的反射谱、吸收系数、损失函数和光电导率

从图7可看到,吸收峰最大值出现在6.91 eV处,为306 536.2cm-1.损失函数描述了当电子快速通过材料时能量的损失,图谱中峰的出现可认为是等离子体激发所致,而峰位则表明了电子被集体激励的频率,从图7还可看到,随着能量的增加,损失函数在18.81eV处达到最大值.光电导是指光照引起电导率改变的现象,从图7可看到,随着能量的增加,光电导率在3.54eV处达到最大值.以上计算结果希望能对研究闪锌矿型HgTe的实验工作有所帮助.

3 结 论

本文采用基于密度泛函理论(DFT)框架下广义梯度近似平面波超软赝势法,优化了闪锌矿型HgTe的几何结构参数,计算并分析了闪锌矿型HgTe的电子结构和光学性质.结果表明,闪锌矿型HgTe为半金属,计算得到其折射率为4.39,静态介电常数为19.24.这为从实验上研究闪锌矿型HgTe电子结构和光学性质之间的关系提供了理论依据.

[1]Clark S J,Wang X Q,Abram R A.Structural and Electronic Properties of HgTe Quantum Dots[C].AIP Conf.Proc.,2005,772:589-590.

[2]孙立忠,陈效双,郭旭光等.CdTe和HgTe能带结构的第一性原理计算[J].红外与毫米波学报,2004,23(4):271-275.

[3]El-Nahass M M,El-Salam F A,Seyam M A M.Optical and Structural Properties of Flash Evaporated HgTe Thin Films[J].J Mater Sci,2006,41:3573-3580.

[4]刘义族,于福聚.GaAs(001)衬底上经双缓冲层生长的Hg1-xCdxTe-HgTe超晶格结构[J].天津师范大学学报:自然科学版,2001,21(3):39-42.

[5]仇志军,桂永胜,疏小舟等.HgTe/HgCdTe量子阱中巨大电子Rashba自旋分裂[J].物理学报,2004,53(4):1186-1190.

[6]Wu K J,Wang M S,Zou J P,et al.Solvothermal Synthesis and Characterization of HgTe Nanoplatelets Using Mercury(I)Source[J].Chinese J Struct Chem,2008,27(4):461-466.

[7]Wang L,Chen X S,Lu W,et al.Optical Properties of Amorphous Semiconductor Mercury Cadmium Telluride from First-Principles Study[J].Sci China Ser E-Tech Sci,2009,52(7):1928-1932.

[8]魏彦锋,王庆学,陈新强等.Hg1-xCdxTe液相外延薄膜的X射线衍射[J].半导体学报,2004,25(8):946-950.

[9]邱岳明,刘 坤,袁诗鑫.HgTe/CdTe超晶格的分子束外延生长和电容-电压谱研究[J].红外与毫米波学报,1994,13(1):73-76.

[10]Rinnerbauer V,Kovalenko M,Lavchiev V,et al.Spectroscopic Ellipsometry of Layer by Layer Deposited Colloidal HgTe Nanocrystals Exhibiting Quantum Confinement[J].Physica E,2006,32:104-107.

[11]Chen X,Mintz A,Hu J,et al.First Principles Studies of Band Offsets at Heterojunctions and of Surface Reconstruction Using Gaussian Dual-space Density Functional Theory[J].J Vac Sci Technol B,1995,13(4):1715-1727.

[12]Sreĉkoviĉ M,Ivanoviĉ N,Ž ižiĉ O,et al.Electrical,Optical,and Thermodynamical Aspects of Sound Propagation in HgTe,HgSe,Hg1-xMnxSe,and MnZn Spinel Ferrites[J].J Electron Mater,2003,32(4):208-214.

[13]王新强,罗 强,何焕典等.HgTe小团簇几何结构与电子性质的第一性原理研究[J].原子与分子物理学报,2006(增刊):140-142.

[14]罗 强,王新强,何焕典等.CdSe和HgTe团簇基态性质的第一性原理计算[J].硅酸盐学报,2008,36(8):1159-1167.

[15]李春霞,党随虎,张可言等.应用第一性原理对CdSe和HgTe团簇结构和电子性质的研究[J].原子与分子物理学报,2008,25(3):542-546.

[16]M an P,Pan D S.Infrared absorption in HgTe[J].Phys Rev B,1991,44(16):8745-8758.

[17]Lu Z W,Singh D,Krakauer H.Total-energy Study of the Equation of State of HgTe and HgSe[J].Phys Rev B,1989,39(14):10154-10161.

[18]Hao A,Yang X,Yu R,et al.Study of Structural Stabilities and Optical Properties of HgTe under High Pressure[J].J Phys Chem Solids,2009,70:433-438.

[19]刘其军,刘正堂,冯丽萍.压力作用下六方钛电子结构和弹性性质的第一性原理计算[J].三峡大学学报:自然科学版,2009,31(4):72-75.

[20]刘其军,刘正堂,冯丽萍等.闪锌矿型CdTe电子结构和光学性质的第一性原理[J].中国科学院研究生院学报,2009,26(5):615-620.

[21]Segall M D,Lindan P J D,Probert M J,et al.Firstprinciples Simulation:Ideas, Illustrations and the Castep Code[J].J Phys:Condens Matter,2002,14:2717-2744.

[22]刘恩科,朱秉升,罗晋生等.半导体物理学[M].7版.北京:电子工业出版社,2008.

[23]Donald Long.Energy Bands in Semiconductors[M].New York:A Division of John Wiley and Sons,1968.

[24]Kuroiwa Y,Aoyagi S,Sawada A,et al.Evidence for Pb-O covalency in tetragonal PbTiO3[J].Phys Rev Lett,2001,87(21):217601-1-217604.

[25]Stampfl C,Van de Walle G.Density-functional Calculations for III-V nitrides Using the Local-density Approximation and the Generalized Gradient Approximation[J].Phys Rev B,1999,59:5521-5535.