基于谱峭度法和自适应遗传算法的轴承故障诊断

张亚洲，石林锁，秦 亮

(第二炮兵工程学院 五系，西安 710025)

包络分析是滚动轴承故障诊断中最有效的工具之一，可以清楚地指示故障的位置以及严重程度，通常应用在信噪比最高的频率范围，这就需要设计优良的带通滤波器以提取故障特征，但不同工况下，振动信号的信噪比最高的频率范围是不同的，因而也需要可变参数的带通滤波器。

谱峭度对淹没于噪声中的非平稳信号非常敏感，能更精确地指示出其发生的频率位置。在此基础上发展而来的基于时频分析的谱峭度法(包括基于STFT[1]和基于WT的谱峭度法[2])，是一种可以有效且自动进行回转机械故障诊断的方法。原始信号经时频分解(或时频滤波器组分解)后，计算其谱峭度值并求最大值，以此最大谱峭度值构造或寻找最优滤波器，对原始信号进行最优滤波，最后结合包络分析法诊断故障。

基于时频分析的谱峭度法能够有效地得到较优的带通滤波器参数。而遗传算法具有泛优化能力，因此，结合谱峭度法和自适应遗传算法，以原始信号经带通滤波器滤波后信号的谱峭度作为适应度函数，建立了滚动轴承故障诊断的一种新方法。

1 基于谱峭度法和自适应遗传算法的包络分析

1.1 带通滤波器参数的编码

包络分析的关键是带通滤波器的设计[3-4]，一个典型带通滤波器的指标要求如图1所示。可知以下参数：以dB计的通带波纹Apass和阻带衰减Astop，通带下限截止频率Fpass1，通带上限截止频率Fpass2，阻带下限截止频率Fstop1和阻带上限截止频率Fstop2便可以表述一个带通滤波器。

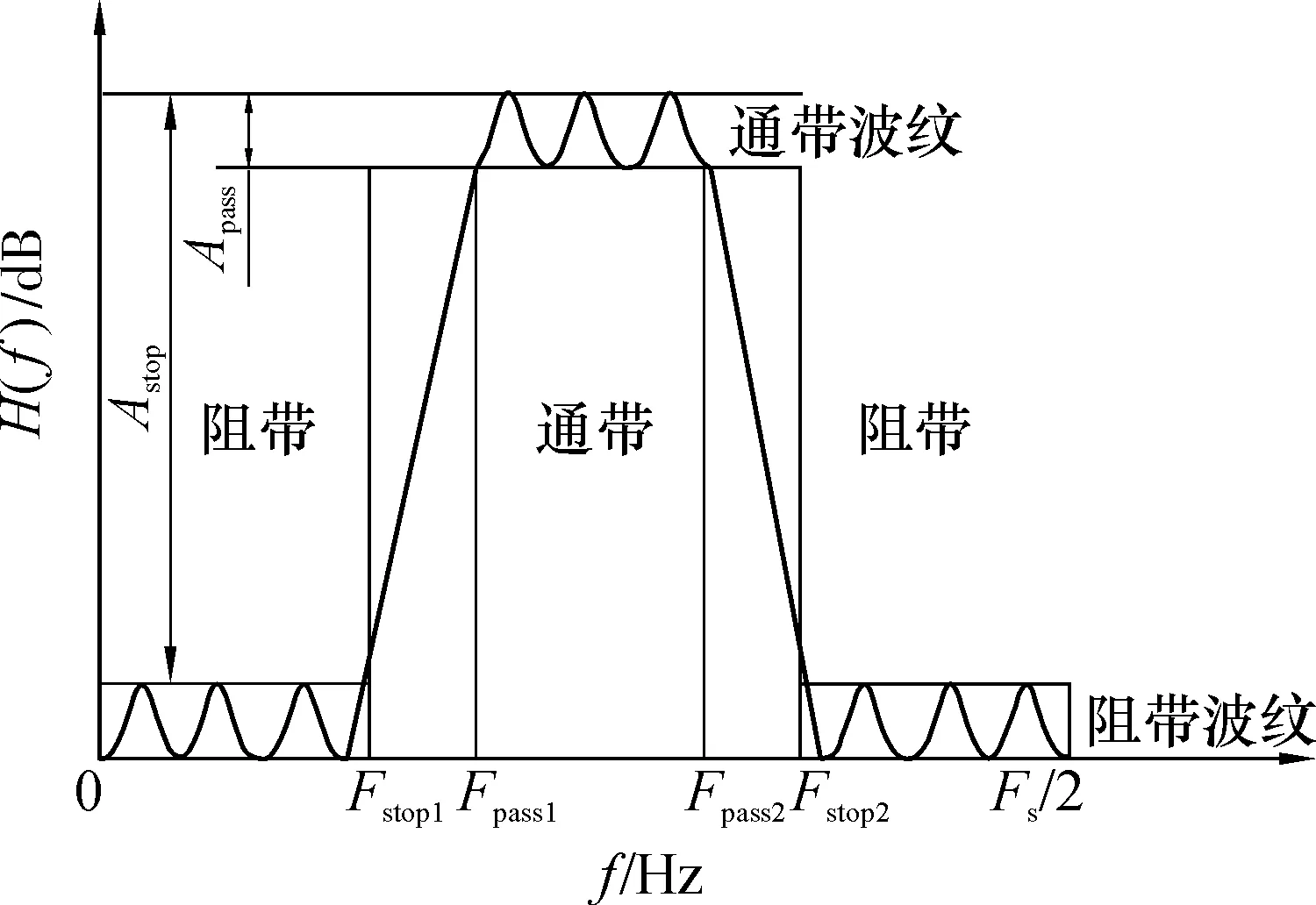
图1 带通滤波器的指标要求

采用二进制编码方法分别对带通滤波器参数进行编码，依次为Astop占7位，Apass占2位，Fpass1，Fpass2，Fstop1和Fstop2分别占10位，共49位。各段二进制编码之间的对应关系为：

(1)

(2)

(3)

(4)

(5)

(6)

其中，chrom(i)是原始种群的一位二进制数；As，Ap，Fs2，Fp2，F0，Fp1和Fs1分别是由基于时频分析的谱峭度法得到的较优的滤波器参数(阻带衰减、通带波纹、阻带上限截止频率、通带上限截止频率、中心频率、通带下限截止频率和阻带下限截止频率)。这样，通过上述二进制编码建立初始种群基因，便确定了一个带通滤波器。本例采用Matlab7中的Parks-McClellan算法设计带通滤波器。

1.2 自适应遗传操作

一旦滤波器的初始种群基因编码实现后，基于谱峭度法和自适应遗传算法(AGA)的包络分析可按图2所示流程进行。

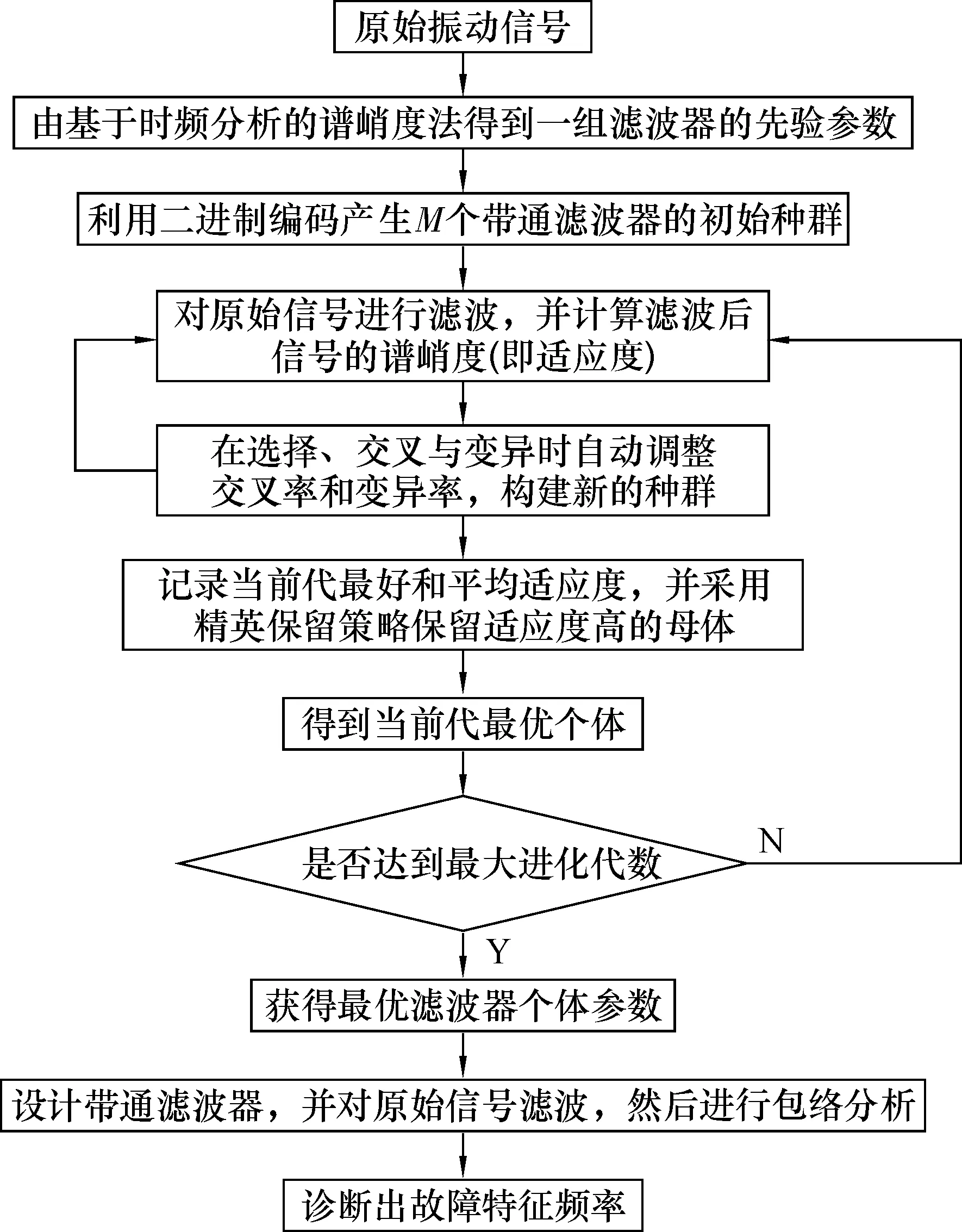
图2 基于谱峭度法和自适应遗传算法的包络分析流程

1.2.1 初始种群的产生

一般产生初始种群的方法有两种：(1)完全随机产生，适用于对问题的解无任何先验知识的情况；(2)将某些先验知识转变为必须满足的一组要求，然后在满足这些要求的解中再随机地选取样本。后一种方法可以使遗传算法更快地到达最优解[5]。

由于在滤波器基因编码中已经加入了从谱峭度法得来的一组先验知识，所以，在此采用完全随机的方法产生初始种群。

根据工程经验，初始种群的规模M在40～100范围内已能满足工程要求[3-4]，为寻求最优效果，在此取M=100。

1.2.2 适应度函数的确定

在故障信号x(t)出现的频率上，谱峭度取大的正值；而在仅含有背景噪声n(t)的频率上，谱峭度近似于取零值。故以原始信号经带通滤波器滤波后信号的谱峭度作为适应度函数。设经带通滤波器滤波后信号的时域平方包络为y=|x|2，则每个滤波器对应的谱峭度值为：

(7)

利用自适应遗传算法全局寻优得到最大谱峭度(即适应度)所对应的就是最优滤波器的参数，由其再设计的带通滤波器对原始信号重新进行滤波，结合包络分析，便可以诊断出故障。

2 工程实测信号分析

分析的实际振动信号在如图3所示的试验装置上采集。齿轮箱的输入轴和输出轴平行布置，均采用KOYO 1205型轴承支承。利用电火花在输出轴承的内圈滚道设置面积大约为3.58 mm2的点蚀。加速度响应传感器(B&K 4508)安装于靠近故障轴承的齿轮箱顶部。在25 N·m的载荷下，轴的转速大约为600 r/min，采样频率为4.8 kHz。滚动体数为12个，滚动体直径7.12 mm，接触角0°，滚子组节圆直径为38.5 mm。计算出轴承内圈故障的特征频率为71.1 Hz。

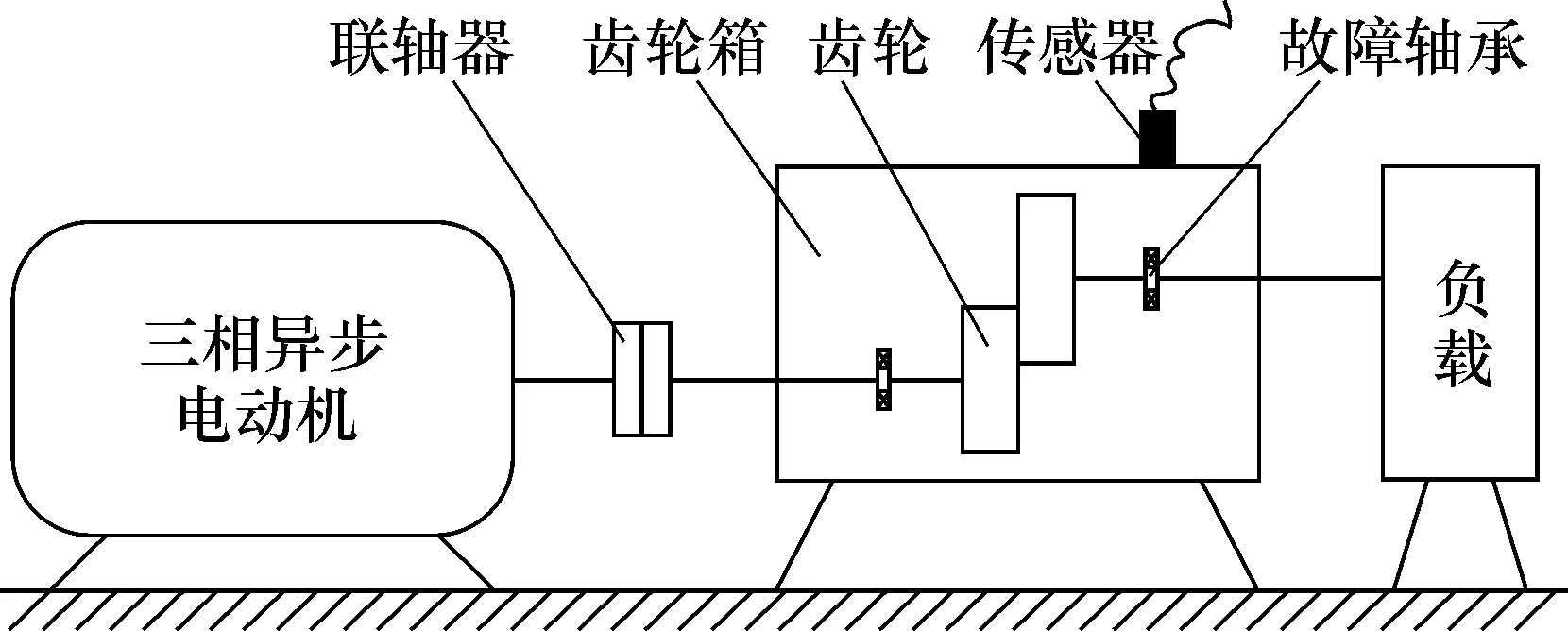
图3 试验装置原理图

首先，由基于STFT的谱峭度法得到一组滤波器的先验参数，见表1。然后，利用基于谱峭度法和自适应遗传算法的包络分析法进行故障诊断。确定初始种群大小M=100，终止进化代数T=200。经过自适应全局优化后，达到优化要求，得到的最优滤波器参数见表1。其历代适应度变化与最优个体如图4所示，而诊断过程与结果如图5所示。从中可以清晰地诊断出轴承内圈故障的特征频率为71.1 Hz。

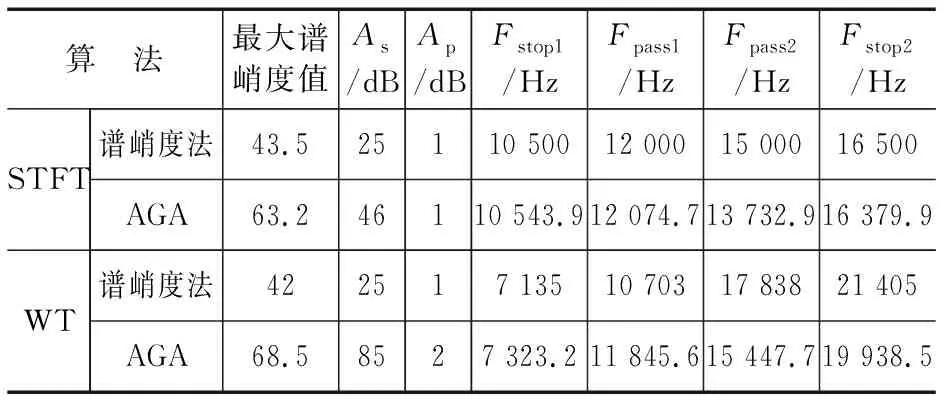
表1 基于谱峭度法和自适应遗传算法的滚动轴承故障诊断结果

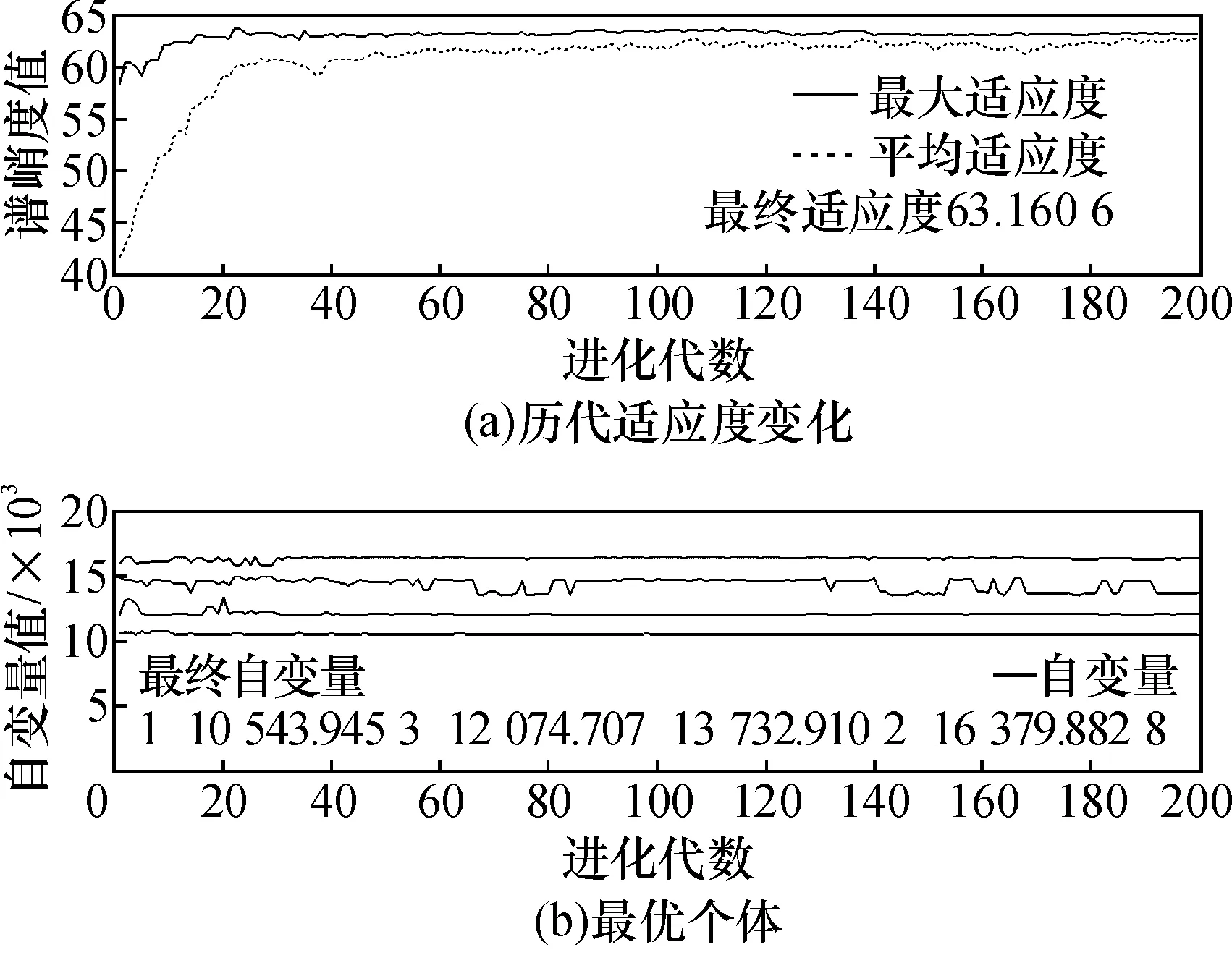
图4 谱峭度法(STFT)结合自适应遗传算法的历代适应度变化与最优个体

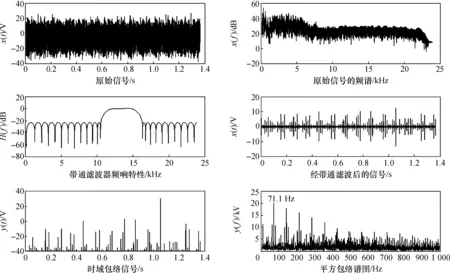
图5 谱峭度法(STFT)结合自适应遗传算法的诊断结果

同样，利用基于WT的谱峭度法得到一组滤波器的先验参数，并经优化后得到最优滤波器参数(表1)。其诊断过程与结果如图6所示，从中亦可以清晰地诊断出轴承内圈故障的特征频率为71.1 Hz。

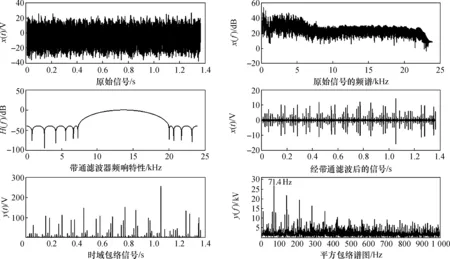
图6 谱峭度法(WT)结合自适应遗传算法的诊断结果

3 结束语

(1)基于谱峭度法和自适应遗传算法的包络分析法是实际可行的，它能够适应变工况下滚动轴承的故障诊断。

(2)与基于时频分析的谱峭度法相比，加入由谱峭度法得到的滤波器先验参数而设计的基于谱峭度法和自适应遗传算法的包络分析法，能够进一步优化带通滤波器，提高滤波后信号的谱峭度，从而更好地诊断滚动轴承的故障。

另外，还进行了基于谱峭度法和基本遗传算法的包络分析法研究，经比较，基于谱峭度法和自适应遗传算法的包络分析法避免了交叉率和变异率的影响，优化效果更好，速度更快，并且降低了对硬件的要求。