大跨度独塔双索面斜拉桥静动载试验研究

2010-07-30蒲黔辉勾红叶

铁道建筑 2010年4期

姜军，蒲黔辉，勾红叶

(西南交通大学，成都 610031)

1 工程概述

泸州泰安长江大桥是泸州绕城高速公路的控制性工程。该桥为独塔双索面斜拉桥，桥梁全长1 543 m，其中引桥为25×40 m预应力混凝土简支T梁桥，主桥为(208+270+35+30)m预应力混凝土箱梁斜拉桥。主桥总宽29.50 m，引桥总宽27.50 m，设计行车速度为60 km/h，设计荷载等级为汽—超20、挂—120级，人群荷载3.5 kN/m2。泸州泰安长江大桥实景见图1。

图1 泸州泰安长江大桥实景

为了验证设计理论和计算分析的可靠性，判断斜拉桥的实际承载能力是否达到设计要求，掌握斜拉桥的组成部份(主梁、塔、拉索)在多种形式车辆动荷载作用下的动反应并积累斜拉桥静、动力反应的技术资料，推动斜拉桥设计、施工、研究的技术进步，本文针对泸州泰安长江大桥主桥进行了理论分析以及静、动载试验研究。并将试验结果与理论分析结果作了比较，结果表明泸州泰安长江大桥的设计计算可靠，施工质量优良，同时结构具有很好的力学性能[1]。

2 理论分析

泸州泰安长江大桥主桥的理论分析计算采用有限元方法。对于斜拉桥的一般计算，采用平面杆系结构有限元方法，需考虑横向作用的分析和结构动力性能及抗震研究采用空间杆系有限元方法。另外，为了更好地考虑斜缆索的整体空间效应，还采用了索面单元，该单元能考虑主梁、塔和索的整体空间刚度，计算出偏载和其它荷载作用下主梁的扭转及翘曲反应。

关于非线性计算，缆索的垂度影响采用了修正弹性模量法(Ernst公式)，而结构的几何非线性影响则采用动态拖动坐标方法来处理[2]。

2.1 普通梁单元

对于一般空间梁单元，每节点有6个自由度，其单元刚度为12×12的方阵。在进行结构的空间计算，如面外风荷载、截面偏载及结构地震反应计算时，要采用空间单元。

2.2 薄壁箱梁单元

一般空间梁单元每节点有6个位移参数和6个杆端力参数。为了反应薄壁箱梁的约束扭转特征，必须增加1个力和1个位移参数，故其单元刚度为14×14的方阵。关于薄壁梁弹性阶段的研究成果很多，而本文薄壁箱梁单元的特点在于:①采用了能同时适用于开口和闭口薄壁结构的弯曲、扭转应变能公式，在此基础上导出的有限元公式对于薄壁结构具有普遍的适用性;②选择薄壁梁弯、扭微分方程的齐次解作为薄壁梁单元的位移插值函数，得到了较为精确的薄壁梁单元的单元刚度矩阵和几何刚度矩阵。用此方法对箱梁进行弹性阶段的分析，避免了板壳元巨大的工作量，也克服了梁格分析方法物理概念模糊的缺陷。与有限条方法相比，该方法更易得到对结构的总体认识与建立明确的物理概念。

3 静载试验

3.1 静载加载设计

试验加载位置与加载工况的确定主要根据设计控制荷载在主梁、主塔上产生的最不利弯矩效应值，按0.80～1.05的效率系数等效换算而得。尽可能用最少的加载车辆达到最大的试验荷载效率，同时应考虑简化加载工况，缩短试验时间。每一加载工况依据某一检验项目为主，兼顾其它检验项目。泸州泰安长江大桥主要针对主桥主跨与边跨主梁的正、负最大弯矩、主塔的最大负弯矩以及斜拉索最大索力作等效加载，静载测点布置见图2。加载过程中采用分级加载，既可以确保结构的安全，同时可以测试偏载工况下结构的受力状况。

3.2 静载测试内容与方法

静载加载工况下主要测试主梁、主塔应力，斜拉索的索力增量，主梁挠度与主塔塔顶变位。应力测试采用粘贴箔式应变计，主梁B-B截面应力测点布置见图2。由电阻应变测量系统测量，温度补偿用搁置在测点附近事先贴好应变花的混凝土块实现补偿［3-4］。斜拉索索力增量采用激振测定法，即在加载前后分别对斜拉索的自振频率进行测量，利用斜拉索的几何材料特性确定的弹性模量推测斜拉索力增量。几何变位测量采用测距精度1 mm+2 ×10－6D(D为测距)，测角精度±2″的全站仪进行极坐标四测回观测。在试验过程中并用温度枪对斜拉索、梁体、主塔进行点温度测量。

3.3 静载试验结果与分析

满载工况下主梁对应截面处的挠度测试结果见表1，偏载工况作用下主梁挠度实测值与偏载效应见表2，主塔塔顶变位测试并与计算结果的比较见表3。表1至表3中挠度数据以向上为正，向下为负，塔偏以泸州方向为正。表3中E工况为主塔最大负弯矩工况。

表1 满载工况下对应截面挠度测试结果 cm

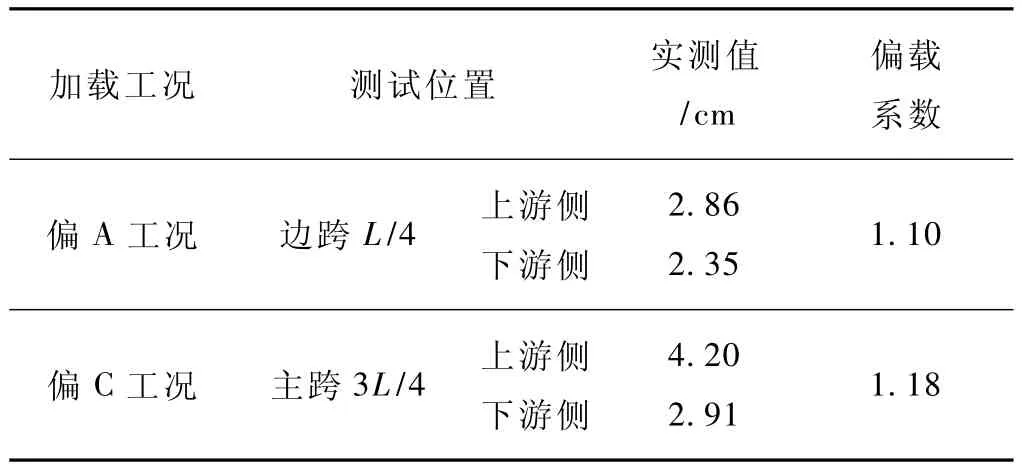
表2 偏载工况作用下主梁挠度实测值与偏载效应

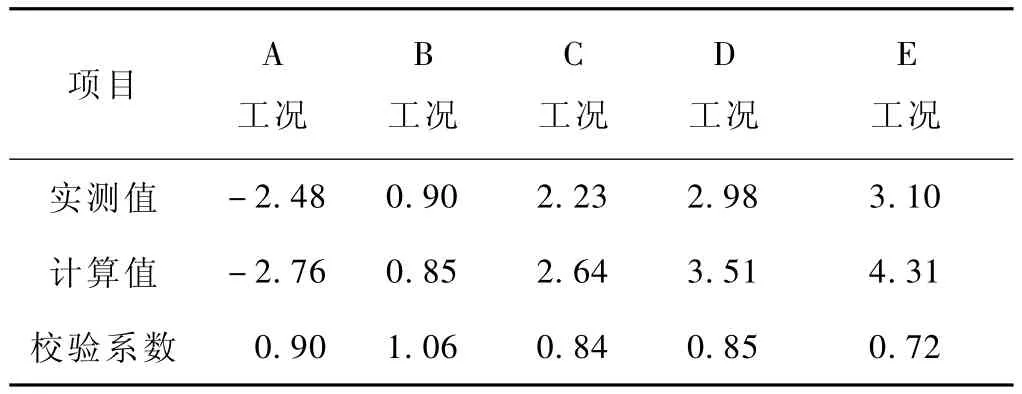
表3 满载工况下主塔塔顶变位结果 cm

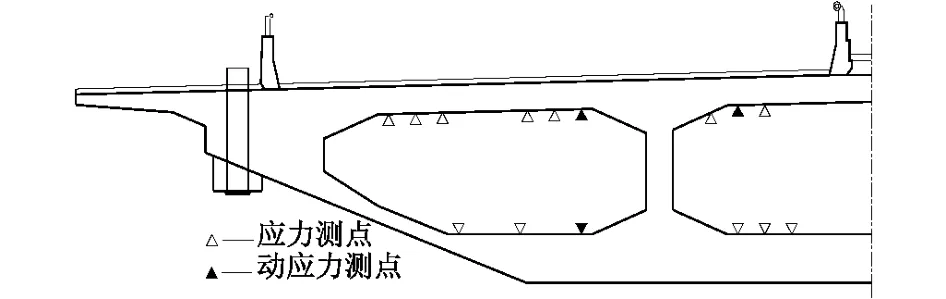
图2 主梁B-B截面应力测点布置

A、B、C、D、E加载工况下挠度的结构校验系数介于0.79～0.87。各工况挠度的结构校验系数均小于1.0，基本在合理范围之内，说明在试验荷载下结构均处于弹性工作状态，也说明主梁的刚度性能良好。偏载工况下，挠度的结构校验系数介于1.10～1.18之间。说明梁体受力有一定的偏载效应，但并不显著，表明箱梁的抗扭性能良好。在各满载工况下，主塔塔顶变位的结构校验系数介于0.72～1.06之间，除B工况的校验系数为1.06外，其余工况均小于1.0，且基本处于合理范围之内。而B工况下塔顶变位的量值很小，因此认为主塔具有较好的整体刚度。

斜拉索索力增量测点布置为对应加载工况下，上、下游两侧各测试5～6对受力最不利斜拉索。在满载工况下，边跨加载A工况测试斜拉索的索力增量校验系数介于0.66～0.88之间;主跨加载C工况测试斜拉索的索力增量校验系数介于0.70～0.89之间。最大索力(主跨23号索)试验工况上下游索力增量校验系数分别为0.72和0.71。索力增量的结构校验系数处于合理范围内，说明索力增量的实测值与计算值相符较好，表明斜拉索受力合理，符合设计要求。

4 动载试验

4.1 自振特性测试结果与分析

自振特性的理论分析采用大型有限元程序ANSYS建立空间梁杆单元模型作模态分析。桥跨结构的实测自振特性与理论计算值的比较见表4，自振频率的实测值和理论值基本相符。存在一定偏差的原因主要是理论计算模型与实际结构的差异以及测试误差的影响。实测结构阻尼较小，说明桥跨结构在环境荷载激励下为小阻尼振动，这和斜拉桥的结构形式是一致的。

表4 实测自振频率与理论计算比较表

4.2 行车激振结果与分析

无障碍行车是重车以10、20、…60 km/h的速度通过桥面，测试主梁A、C截面处的动态应变。有障碍行车是重车以5、10、15、…30 km/h的速度通过设置障碍的桥面，测试主梁A、C截面处的动态应变。行车激振下实测主梁动应变时程曲线见图3、图4。

图3 40 km/h无障碍行车时C截面上缘测点应变时程曲线

A截面无障碍行车测点实测冲击系数(1+μ)介于1.04～1.15之间，最大值出现在时速为40 km/h时，其值为1.15。C截面无障碍行车测点实测冲击系数(1+μ)介于1.06～1.15之间，最大值出现在时速为50 km/h时，其值为1.15。可见无障碍行车对主梁的冲击系数很小，说明当桥面平整时，桥面行车对桥跨结构的冲击作用很小。

图4 20 km/h障碍行车时C截面上缘测点应变时程曲线

A截面有障碍行车测点实测冲击系数(1+μ)介于1.14～1.50之间，最大值出现在时速为10 km/h时，其值为1.50，冲击系数相对较大，说明行车对A截面处的冲击作用明显。C截面有障碍行车测点实测冲击系数(1+μ)介于1.12～1.30之间，最大值出现在时速为15 km/h时，其值为1.30，冲击系数也相对较大，说明行车对C截面的冲击明显。有障碍行车试验表明:当桥面不平整时，桥面行车对桥跨结构的冲击作用将明显增大。

车辆对桥跨结构的冲击作用缘于三个方面:车辆自身的振动，桥面不平引起车辆的振动，车辆作为移动力对桥跨结构产生的广义扰动力作用，而这三个作用又是相互耦合相互促进的。对于公路桥梁来说，桥面不平整引起的冲击作用则是主要的。