基于曲线拟合单位线法的桥梁水害预测
2010-07-30崔阳华文雨松
崔阳华,文雨松
(中南大学 土木建筑学院,长沙 410075)
1 问题的提出
近年来桥梁事故时有发生,从调查结果来看,这些桥梁很少是被车辆荷载破坏的,往往是被洪水冲毁的。据交通部1995~1997年统计[1],这三年我国平均每年公路水毁的直接经济损失达52亿元,其中水毁桥梁达3945座。2006年截至8月8日,广东省公路中断1149处539条,其中国省道中断383处121条;桥梁冲毁113座,局部毁坏638座。2007年,我国南方省份公路、桥梁等交通基础设施水毁严重。据交通部初步统计,截至7月中旬,全国共18个省(区、市)发生公路水毁,先后有3条高速公路、79条国道、409条省道出现局部交通中断,造成经济损失几十亿元。
由于许多既有桥梁已建年代久远,用一般方法鉴定其抗洪能力时,收集水文资料存在很大的难度。即使是保存有原始的水文资料,由于修桥后经长期运营和自然演变,其周围的自然环境,包括地形、地貌及植被等,都已经发生了变化[2],设计桥梁时的水文资料也不能很好的表征现在的河流状况,难以进行水害预测。因此,在缺乏水文实测资料的不利因素下,能否寻求一种比较简便的方法,用于既有中小桥水害预测,是人们非常关心的问题。
现行中小桥抗洪能力预测方法普遍采用从雨量到流量、再从流量到水位的方法。对于求流量的方法,根据桥梁所在地,有地区经验公式法、推理公式法、单位线法、铁路设计院法等[3]。对于由流量推求水位的方法,多采用谢才—满宁公式计算。这种方法需要确定过水断面面积 A、水力比降 i、糙率系数 n等参数[4],劳动强度大、收集困难多。特别对于很多没有水文观测站的中小桥,由于资料的缺乏,实现难度很大。在《基于水位单位线和桥墩水痕的既有中小桥水害预测》[5]一文中,提出了水位单位线法,克服了许多中小桥缺乏实测资料的不利因素,而且比较简便。
从降雨到洪水的形成,往往需要一定的时间,即造峰期。而在洪灾发生前的这段时间就非常珍贵,如果在灾害发生前,能提前几分钟甚至几小时做出预测,并及时防护,就可以挽救很多宝贵的生命和减少灾害对国家财产造成的重大损失。
但是文献[5] 方法求得的都是整数时段的水位值,并且间隔时间过长,一般都在3 h以上。在实际情况中,会出现最大水位值在两个整数时段中间的情况,这样上述方法关于时间的预测就不是很准确,对于桥梁水害预防来说有很大影响。
基于上述原因,本文从单位线法公式出发,提出了一种以曲线拟合单位线为基础推求洪水到达时间的新方法。即利用实测水位和雨量,拟合出以水位和时间为记录对象的水位单位线,再利用计算出的水位单位线直接预测洪水水位的到达时间,在洪水到来之前的这段宝贵时间内就可以进行合理的防灾调配,对有危险的桥梁进行保护。
2 曲线拟合单位线法的推导
参照单位线的两个基本假定,仍认为水位单位线服从两个基本假定。根据水位过程线的形成过程,水位单位线的推求可依下式进行:
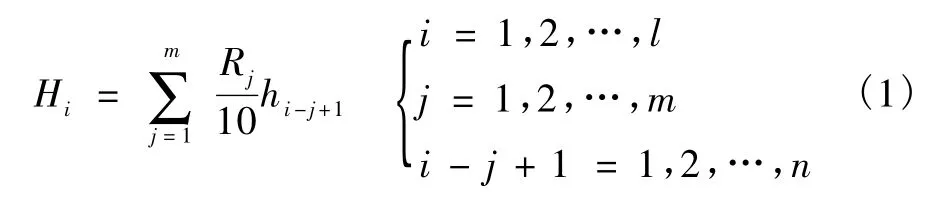
式中 Hi——流域出口断面i时刻水位值,单位 m;
Rj——流域上 j时刻净雨量,mm;
hi-j+1——水位单位线(i- j+1)时刻纵坐标,m;
l——流域出口断面水位过程线时段数,l=n+m-1;
m——净雨时段数;
n——水位单位线时段数。则有如下线性方程组

其中用[R]来表示系数矩阵(净雨量),用[h]来表示未知数向量(单位线),用[H]来表示水位过程向量,求解方程组式,其解为
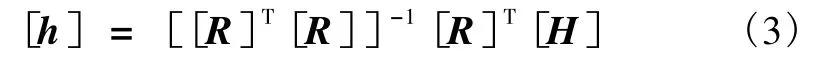
式中的[R]T为[R]的转置。
最小二乘法推求的单位线数值,可得到误差最小的唯一解。但是仍可能出现单位线呈锯齿跳动,或出现负值的不合理现象,并且极值不在整数时段上的情况,所以应对其修正。这里采用拉格朗日插值和用多项式作最小二乘曲线拟合的方法[6]。
首先进行最小二乘曲线拟合,设拟合的曲线方程为
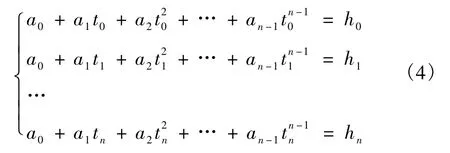
对全部数据进行拟合的话,很可能会出现最大值不在所求曲线方程上的情况,所以,选取hmax附近的5个点进行拟合,采用高斯—若当全主元消去法可求得方程组的解,则最小二乘数据拟合多项式为
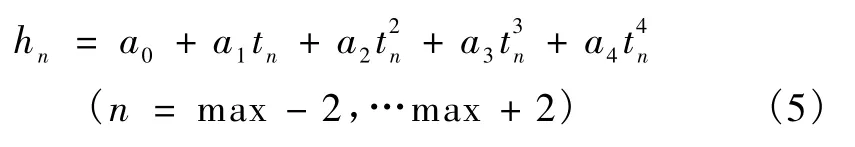
拉格朗日插值多项式对非线性曲线上的任意x值可以求得其对应的函数值,并且达到一定的精度,设插值多项式为

分别代入 (t0,h0)…(tmax-2,hmax-2) 和 (tmax+2,hmax+2)…(tn,hn),即可求得 Ln1(x) 和 Ln2(x),与前面的所得方程,即为水位单位线。
由水位单位线[7],在降雨来临的时候,只要获得未来雨量的预测值,就可以确定相应的水位值,而且根据水位与时间的对应关系,就可以得出每个水位到来的时间,进行水位与时间预测。
3 水位单位线法预测实例
浙江某县水文站的一场洪水,有2个时段降雨,计算时段长Δt=3 h。由流量资料,得知实际上洪峰可能为9~12 h或12~15 h之间到达,但是具体的时间确定不了,即使确定了,时间间隔也很大。下面用新方法进行计算,见表1。
选取计算出的单位线数据,进行拟合,得到以下方程[8]
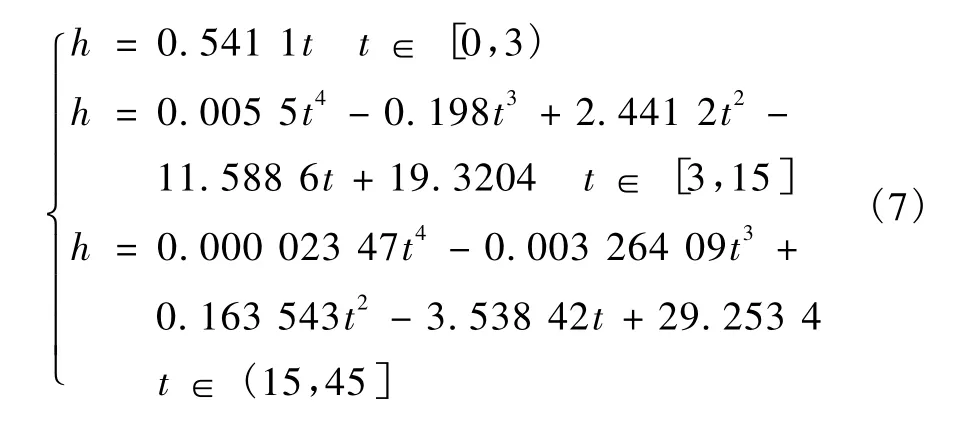
此为拟合出的水位单位线的曲线方程,选取适当的点,得到单位线的图形见图1。
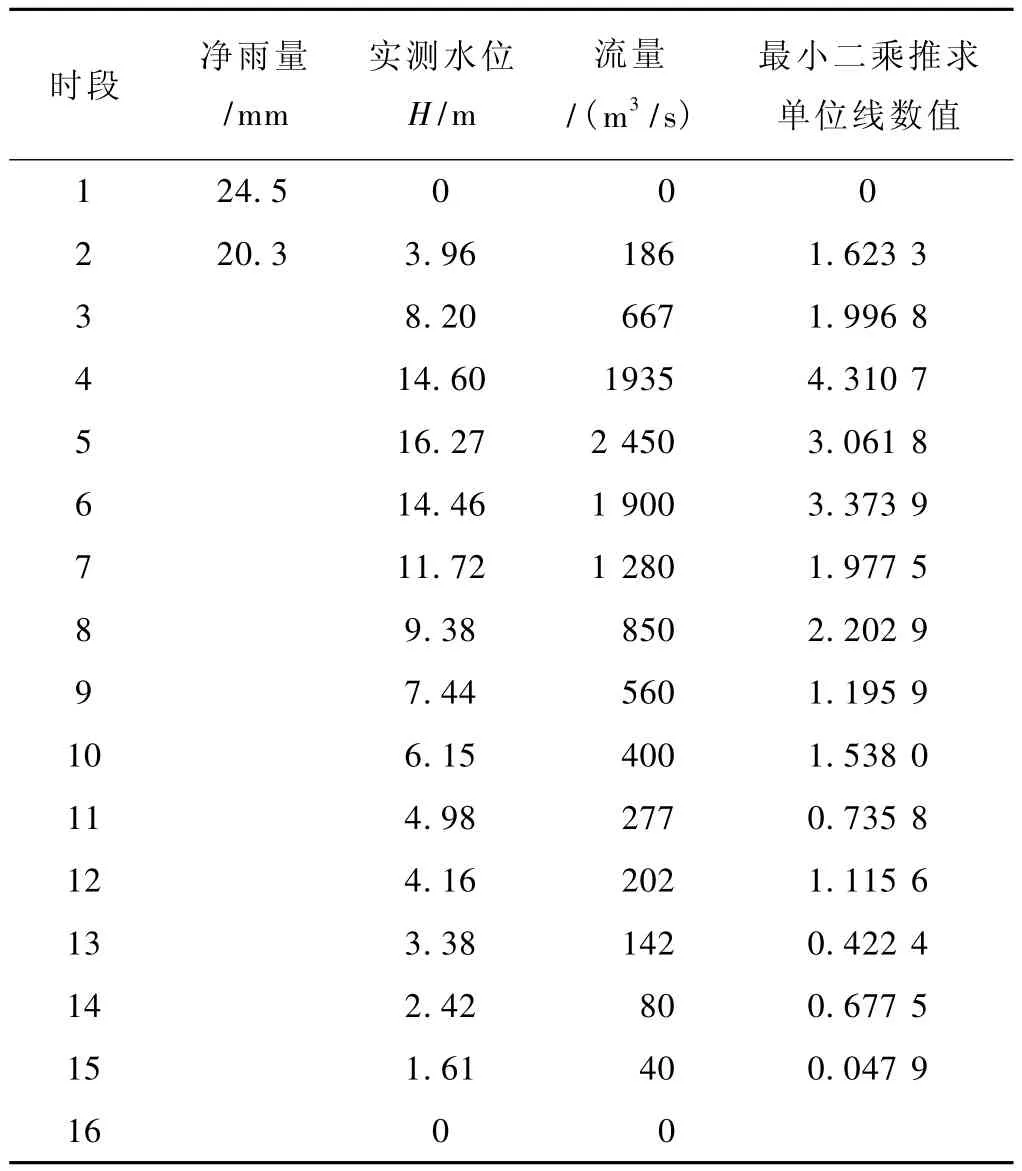
表1 最小二乘法推求单位线数值
当有了以上所得结果,在工作中,当得知雨量的时候,可以由水位单位线推出洪峰到来的时间为11个小时之后,水位为19.477 8 m,时间和水位值相比于以前的方法都更加精确。如洪水超过了设计水位,就可以提前做好救灾物资调配,安排好抗洪抢险队伍,进行有效的桥梁水害预防。

图1 对数据拟合得到的水位单位线
有了水位单位线,就可以对此桥新的雨量进行洪峰预测。某日有3个时段降雨,计算时段长Δt=3 h,见表2。

表2 实测净雨和水位数据
经计算,预测洪峰为13 h之后到达,洪峰水位为18.729 92 m,与实际洪峰水位相符(见表3),而且可以看到,相对误差控制在10%以内,可以满足实际要求。
4 结论
1)为了解决其他方法存在的时间间隔大、洪峰可能漏测的问题,本文首次提出了曲线拟合单位线法。如果需要,在时间上甚至可以精确到10 min。
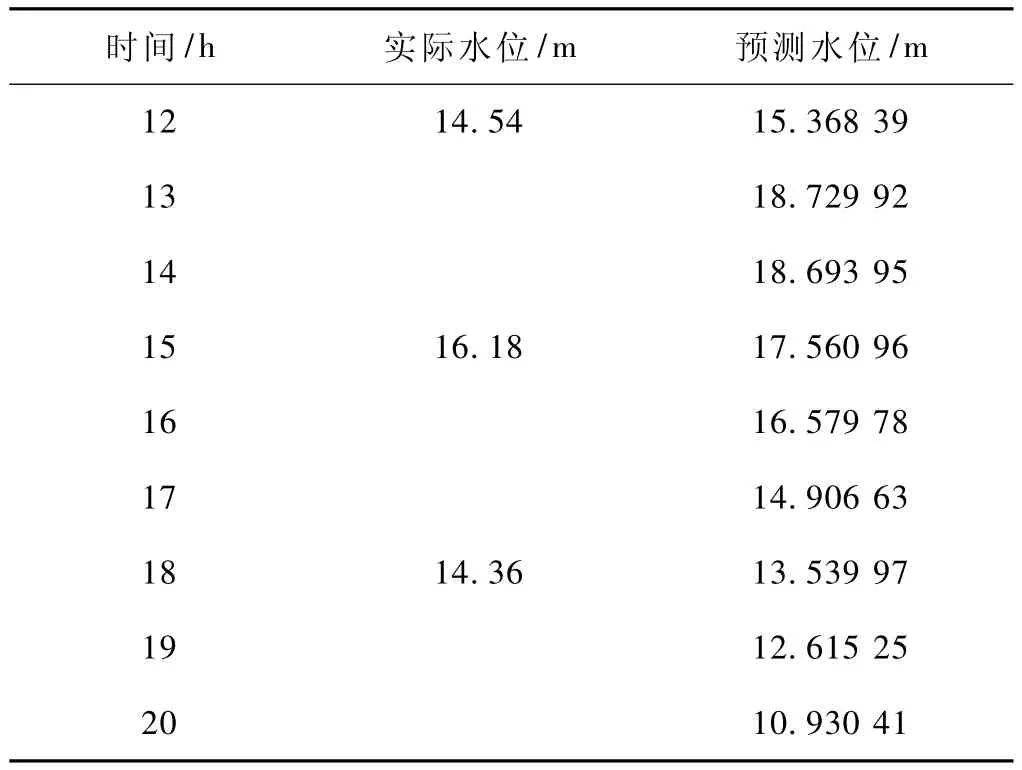
表3 预测水位和时间
2)本文采用最小二乘法和拉格朗日插值法进行曲线拟合,概念清晰。因为得到了曲线函数,所以可以预测出洪峰的到来时间。相比于以前的方法时间间隔短,拟合出的数据对灾害预防更加有实际意义。特别是高水位区,相对误差绝对值控制在10%以内,能够满足实际生产的要求。
3)本文在水位单位线法不用收集流域面积、流域坡度、主河道长度、河床糙率、桥位断面数据等优点的基础上,水位和时间计算更加准确,此方法具有更高的实用价值和更广阔的应用前景。
[1] 黄朝迎,张清.暴雨洪水灾害对公路交通的影响[J].气象,2000,26(9):12-14.
[2] 王中强,文雨松.原始断面的模糊识辨方法[J].长沙铁道学院学报,2002,20(3):30-34.
[3] 文雨松.桥涵水文[M].北京:中国铁道出版社,2005.
[4] 廖松,王燕生,王路.工程水文学[M].北京.清华大学出版社.1991.
[5] 曹二星,文雨松.基于水位单位线和桥墩水痕的既有中小桥水害预测[J].铁道建筑,2008(9):22-25.
[6] 肖筱南.现代数值计算方法[M].北京:北京大学出版社,2003.
[7] 庄一鸽,林三益.水文预报[M].北京:水利电力出版社,1986.
[8] 沈剑华.数值计算基础[M].上海:同济大学出版社,2005.
