钢管混凝土轴心受压短柱承载力概率分布研究
2010-07-30徐腾飞向天宇赵人达
徐腾飞,向天宇,赵人达
(西南交通大学 桥梁工程系,成都 610031)
钢管混凝土构件由于受力过程中在钢管和混凝土之间产生了紧箍力,改善了整体工作性能,使钢管混凝土结构具有一系列优越的性能,在公路及铁路桥梁中有广阔的应用前景[1-2]。利用可靠度研究方法,可以考虑构件抗力的随机性,更加真实地反应钢管混凝土构件的承载能力。韩林海对钢管混凝土构件(包括短柱、长柱和中长柱)的可靠度问题展开系统研究[2],该研究对钢管混凝土轴压、偏压、纯弯与压弯构件进行可靠度分析。由于钢管混凝土短柱极限承载能力公式比较复杂,含有多个随机变量,进行可靠度分析时多采用一次二阶矩法或蒙特卡洛模拟方法。当失效面的形状和n维超平面偏离较大时,一次二阶矩法的计算误差将显著增大,且对误差的界限无法估计[3]。极限状态方程的非线性程度很高时,可靠度指标宜采用更精确的方法计算,例如蒙特卡罗方法[4]。而为了获得足够的精度,尤其是小失效概率时,蒙特卡罗方法需进行大量的抽样,这将消耗大量的机时与引入大周期随机数生成问题,制约了其在工程上的应用。
本文利用《钢管混凝土结构设计与施工规程》中的钢管混凝土极限承载力公式与蒙特卡罗方法研究了钢管混凝土轴压短柱极限承载能力的概率分布,并回归得到了钢管混凝土轴压短柱构件承载能力的均值与方差的表达式,利用该分布模型可以简化钢管混凝土短柱可靠度指标的计算。
1 钢管混凝土轴压短柱极限承载能力
钢管混凝土轴压短柱极限承载能力公式为[5]
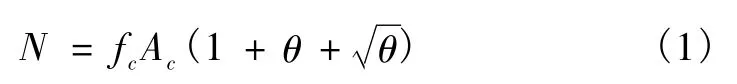
式中,N为轴心受压短柱承载能力;fc为混凝土的轴心抗压强度;Ac为核心混凝土面积;θ为钢管混凝土套箍系数,θ=fsAs/(fcAc)(fs为钢管的屈服强度;As为钢管的面积)。
将式(1)整理得到式中,变量上方加“-”表示该变量的均值;¯θ为钢管混凝土套箍系数均值,;D为钢管的直径;t为钢管的厚度。
将式(2)中的随机变量做如下无量纲处理


式(2)的无量纲形式为
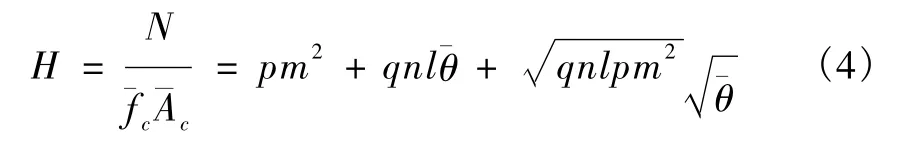
由文献[6-7]可知,变量 fy,fc均满足正态分布,则变量p、q是均值为1.0的正态分布变量,变异系数如表1所示。变量 D、t满足正态分布,变异系数 δD、δt为0.05[2]。假设 D、t相互独立,则随机变量 m、n、l是均值为1.0的正态分布变量,其均方差可写为

在绝大多数情况下,D≫t,式(5)和式(7)可简化为
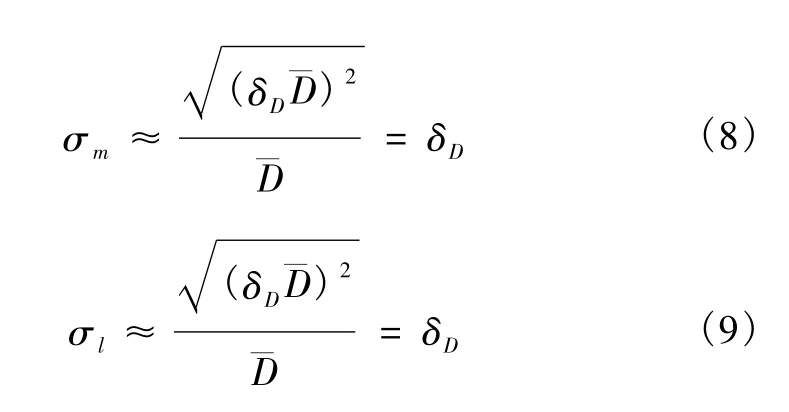

表1 变量 p、q的变异系数 δp、δq
2 极限承载力概率分布
一般情况下,钢管混凝土的套箍系数不宜大于4,也不宜小于0.3[2]。本文利用蒙特卡罗方法(抽样次数100万次)计算H函数的概率密度函数,以套箍系数作为参数,对常见钢材牌号与混凝土标号分别计算。按照置信率0.01进行H函数的K-S检验。结果表明,H函数不拒绝正态分布。
图1给出了H函数的抽样概率密度函数fH(图1中曲线自左向右,套箍系数依次为0.3、0.6、…、3.9),由图1可以看出,随着套箍系数的增大,钢管混凝土短柱轴压承载能力的均值与离散性均逐渐增大。图2给出了H函数的均方差与套箍系数的关系,由图2中可以看出,采用相同钢材的C40与C50钢管混凝土的均方差比较吻合,这是由于C40与C50混凝土材料变异系数相差不大,回归分析得到均方差函数为

对于不同材料的钢管混凝土柱,H函数均值的回归结果基本一致,回归公式为
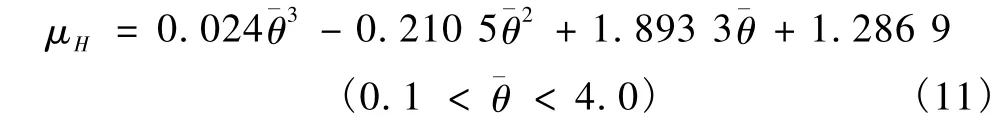
由H的概率特性可知,钢管混凝土短柱的轴心抗压承载能力服从分布。采用该分布可以直接计算结构承载能力的可靠度指标。
以直径D为100 mm,组成材料为 Q235与C60的钢管混凝土短柱为例,定义功能函数

式中,R和S分别为结构抗力和荷载效应。在给定S的情况下,可靠度指标可表示为

图3给出了不同壁厚t下的承载能力可靠度计算结果。作为对比,同时给出了对式(1)进行重点抽样[10]得到的可靠度指标结果,可以看出本文方法与重要抽样法计算的可靠度指标比较吻合,但是由于本文方法有一定的近似性,在小失效概率的情况下,与重要抽样计算有一定差距。

图1 H概率密度的函数

图2 H函数的均方差与套箍系数关系
3 结论
本文利用蒙特卡罗方法,考察了钢管混凝土短柱轴压极限承载能力概率分布。数值分析表明,其分布不拒绝正态分布。由抽样结果和回归分析得到了钢管混凝土短柱承载能力分布的均值与方差。随着套箍系数均值的增大,承载能力均值增大,分布的离散性也随之增大。本文提出的钢管混凝土轴心抗压承载能力概率分布模型,可用于简化钢管混凝土结构的可靠度指标计算。
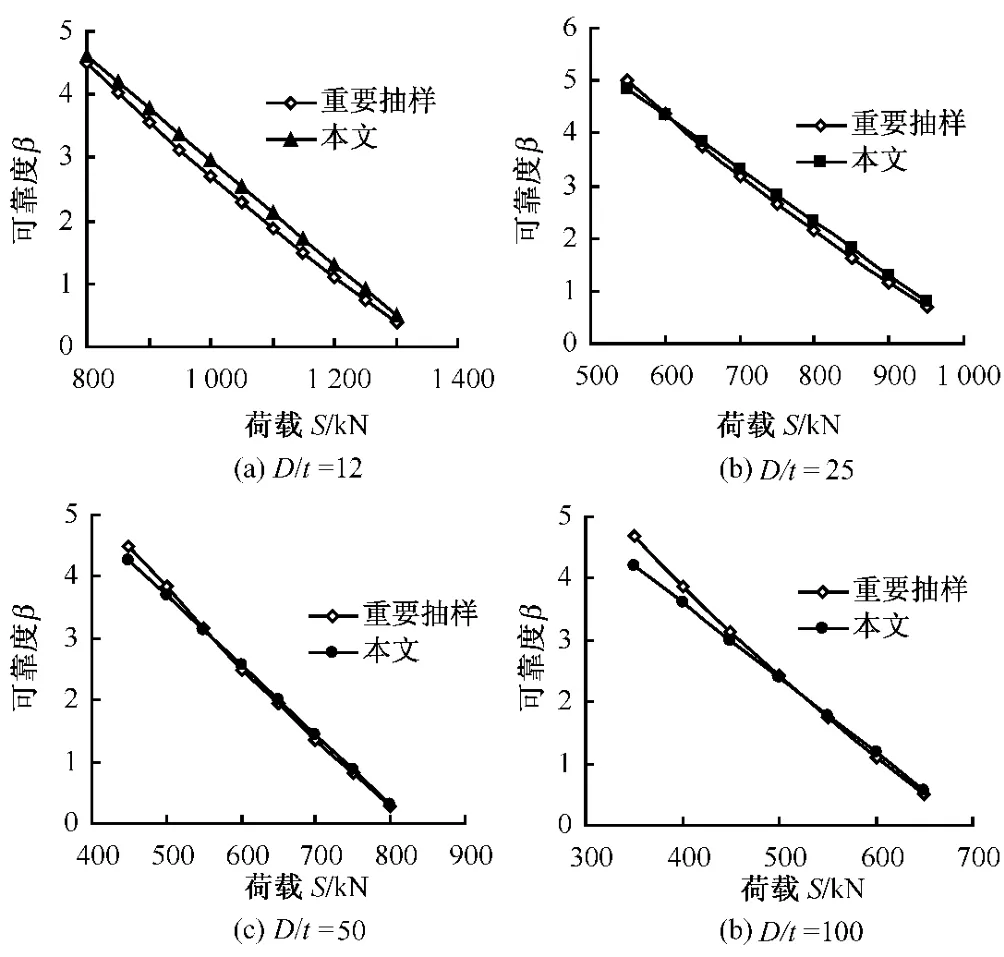
图3 可靠度指标计算比较
[1] 钟善桐.钢管混凝土结构[M].哈尔滨:黑龙江科学技术出版社,1994.
[2] 韩林海.钢管混凝土结构——理论与实践[M].北京:科学出版社,2004.
[3] 董聪,刘西拉.非线性结构系统可靠性理论及其模拟算法[J]. 土木工程学报,1998,31(31):33-42.
[4] 周圣斌.钢管混凝土柱极限承载力可靠度校准分析[J].建筑科学,2009,25(3):79-81.
[5] 中华人民共和国建设部.CECS 28:90 钢管混凝土结构设计与施工规程[S].北京:中国建筑工业出版社,1990.
[6] 赵国藩,金伟良,贡金鑫.结构可靠度理论[M].北京:中国建筑工业出版社,1990.
[7] 中华人民共和国建设部.GB 50010—2002 混凝土结构设计规范[S].北京:中国建筑工业出版社,2002.
[8] 陶忠,韩林海,杨华.钢管混凝土构件设计计算及可靠度分析[J]. 工业建筑,2000,30(6):1-6.
[9] MELCHERS R E. Structural reliability analysis and prediction[M].New York:John Wiley & Sons,1999.
[10] XIANG T, ZHAO R. Reliabilityevaluation ofchloride diffusion in fatigue damaged concrete[J].Engineering Structures,2007(29):1539-1547.
