大功率永磁电机温度场数值计算及实测对比
2010-07-25刘万平张新丽赵祥张世福
刘万平 张新丽 赵祥 张世福
(新疆金风科技股份有限公司,新疆 乌鲁木齐 830026)
1 引言
电机运行时会在线圈、铁心等部件上产生能量损耗,这部分损耗最终都将以热能的形式散发出去。如果电机的通风冷却设计不合理,就会使电机内部温度不能保持在合理的范围内,温升过高会导致绝缘老化,长时间运行时会使绝缘电气性能下降;同时局部温升不均匀,还会产生很大的热应力,造成电机结构上的永久性损害,最终导致的发电机故障,会直接影响用户的使用。因而温升是考核同步电机的一个重要指标。
目前温升的主要计算方法有三种:简化公式法[1]、等效热路法[2]和温度场法[3-4]。简化公式法是电机制造厂常用方法,首先计算出各部分的热负载,再通过牛顿散热公式得到相应的温升值。这种方法计算简单,但只能计算电机的平均温升,计算结果不太精确。等效热路法是根据传热学和电路理论来形成等效热路,热路图中的热源为绕组的铜损耗和铁损耗,这些损耗所在部件在计算中认为是均质的。损耗热量通过各种相应的热阻,由热源向冷却介质传递,形成一个复杂的热网络。此方法计算精度要高于简化公式法,但如果提高精度,必需增加网络节点和热阻数,使工作量增大[5-6]。温度场是现代数值方法来求解热传导方程,将求解区域离散成许多小单元后,在每个单元中建立方程,再对总体方程组进行求解。其优点是将研究对象从总体转为局部单元,使每个局部单元都能获得可靠的计算数据,从而更加准确合理地指导电机设计,缺点是计算量大,不适合用在设计初期的选型计算中。
本文以金风科技股份有限公司自主研发的3MW永磁同步发电机为实例,重点介绍热路法,并分别采用热路法和有限元方法对其在不同负载条件下的温度场进行了计算,并将计算结果与实测数据进行了对比,验证了热路法的可行性。
2 热路法计算发电机温升
2.1 基础理论
一个实体热源可通过三维空间上不同的面将热量传送出去。假设图1所示的均匀发热体内单位时间的发热量为P,其内部中心温升为T,发热体的热导率为λ,则可近似认为单位时间的等效热流量P将会沿着xyz六个方向传送出去。
假设通过x正方向传送的热量为Px,壁面温度为Tx1,则试验证明,传过平壁的每单位时间热量Px与面积S,温度差(T-Tx1)成正比,与壁厚(Lx/2)成反比[7],即:


图1 发热量为P的均匀发热体
式1即为热传导基本定律。
这样,类似欧姆定律,可以将温差看做是电路中的电压,单位时间的传输热量相当于电路中的电流,而热阻则相当于电路中的电阻。如果我们把电机分为n个这样的发热体,则每个发热体都可建立类似式1的方程,将n个方程联合求解,在热阻和热流量已知的情况下,可求解得到各点温度。如果电机离散成足够多的单元,则计算精度可以满足我们的要求。
我们也可从图2中看到一个单元之间热阻、温度及热流量之间的关系,即热网络图。假设发热体中的单位时间内所有热流量P从i点注入整个系统,并等效从6个方向散发出去。每个方向所遇的热阻可通过面积导热率及壁厚得到,如式2。而-1/6Rx、-1/6Ry、-1/6Rz为各方向的耦合热阻。

图2 热网络图
2.2 电机热路场分析模型
本文中的算例电机为金风自主研发的3 MW风力发电机组用三相永磁同步发电机,电机额定功率为3200 kW。冷却方式为IC666[8],即电机为空空冷却,一次冷却介质空气在独立外装风扇的作用下强迫电机内部空气循环流动,二次冷却介质为电机周围环境介质,也在独立外装风扇的作用下驱动周围冷却空气流动,从而使电机的发热功率最终通过二次冷却空气带走。
根据上述方法,对算例电机进行热网络分析,主要求解包括绕组、铁心和磁钢等地方的温升,对电机的温升设计进行校核。
在计算前做如下假设:
(1)电机定子共120个槽,以每个齿槽为一个单元,假设在圆周上单元与单元之间不存在热交换, 而温度差只在一个单元之内的齿、槽内分布;
(2)电机定子轴向均匀分成20段,为径向通风冷却,假设冷却系统沿轴向完全对称,铁心段之间不存在热交换,而两端部绕组温度场分布情况完全一致;
(3)电机内发热部分仅存在于上、下层绕组、铁心、转子磁轭和磁钢上,并假设为均匀发热体,其它电机部件上无损耗;
(4)电机内部的热流量方向为三维方向;
(5)电机所有冷却气体的温升相同,并按照下式进行计算。
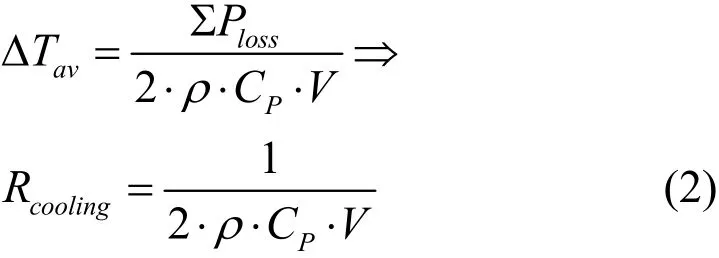
其中,V是气体的总流量,经过磁钢、绕组、定子齿部和转子轭部后所有冷却气体的平均温升为△Tav。
按照图 2所示方法,将电机主要发热体等效为热网络图,并将并联和串联的热阻进行简化,这样电机热网络图可表示为图3中的简化模型。
图3中所示各项的表示意义如下:
P1、P3、P9分别对应于轭部区域、齿部下层、和齿部上层单位时间等效热流量;P2为槽底下对应的铁心处单位时间等效热流量;P10、P4分别对应上下层绕组槽内单位时间热流量;P7、P8为磁钢和转子磁轭处的单位热流量,P5、P6、P11为求解方程时所需要的虚拟连接点,此点的热流量设为0。
图 3中所有热阻为简化后的值,分别代表各发热单元之间的等效热阻。

图3 一个齿槽内的热阻简化模型
I表示定子外圆处的通风区域,II表示与下层绕组端部相连,III表示与上层绕组的端部相连,IV表示转子内圆表面的区域,V表示与通风道相连的区域。
由于篇幅所限,在这里没有给出绕组端部的等效热网络,其建模方式与定转子建模方式相同。
2.3 计算过程与计算结果
根据电机实际运行环境及运行损耗,输入如下接口参数:

表1 3 MW永磁发电机温升计算接口参数
电机铁心、绕组等各部件的导热参数可根据查取相关材料特性手册得到。而电机对流换热系数的求解可分成三种,定转子铁心表面非强迫风冷的地方为自然对流换热方式,因而求解得到的是自然对流换热系数;通风道内(包含齿部、轭部、气隙)等地方为强迫对流换热方式,可根据风速求解得到相应的强迫对流换热系数;而在端部由于线圈端部连接形式复杂,通常采用经验系数来确定对流换热系数。
3 有限元模型
有限元方法是目前用来计算电机温升的常规方法,本文采用有限元方法,对3 MW永磁同步发电机的三维流场、温度场进行计算。考虑几何模型的对称性,只对四分之一几何模型进行分析,计算流体部分的流场分布。然后,从流体部分的流场分布中找到速度最小的流场通道,针对该通道进行网格局部划分,并精细网格。采用 mpcci商业软件进行流固耦合计算,分别用abaqus软件进行固体部分计算,fluent软件进行流体部分计算,从而达到整个流场的温度分布。
网格剖分图如图 4。为了保证计算精度及考虑经济性,采用全六面体网格划分策略,此四分之一的电机模型需要网格数为400万。

图4 网格剖分图
图5中给出了温度场计算结果,有限元计算结果与热路法计算结果见表 2。可以看出除转子磁轭外,绝大部分的平均温升差值在 5℃以内。而之所以磁轭部分温升相差较大,是由于热路法计算中无法计及冷却气体经过电机不同部件后的温度改变。在热路法中,认为冷却气体的温升均为经过所有部件后的平均温升,因而经过磁轭时冷却气的温升计算偏高,导致磁轭处的温升比实际值偏大。

图5 温度场计算结果
4 实测对比
在全功率试验台上对3 MW永磁发电机做温升试验,试验台组成:两台1600 kW 的直流电动机并联拖动齿轮箱1, 经扭矩仪(30000 Nm)、过渡支撑、万向节、齿轮箱2、3 MW 永磁同步发电机、3MW ABB 变流器、升压变压器及调压器后并入电网,其它设备包括电流互感器CT(精度0.2 级)等测试仪器。

表2 热路法与有限元法的计算对比

图6 全功率试验台
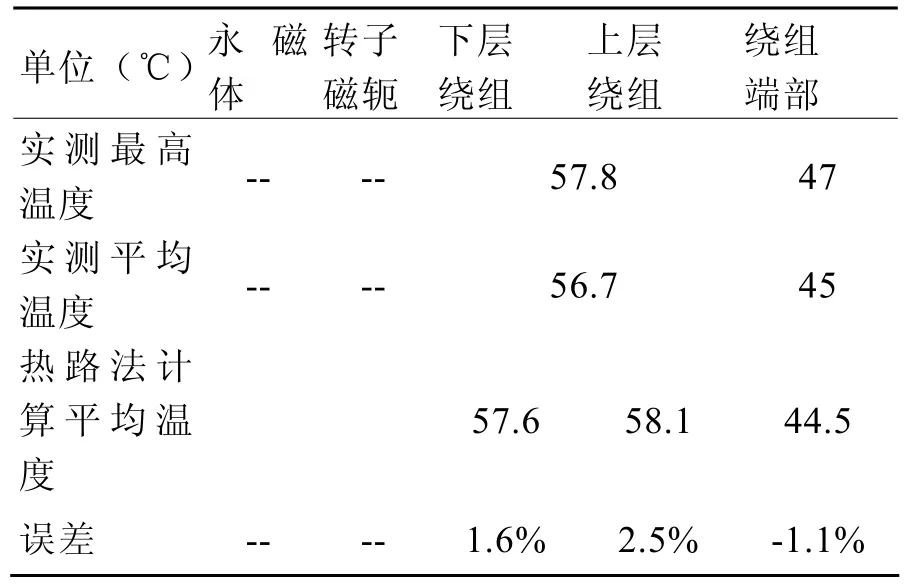
表3 热路法计算与实测温升数据对比
在电机温升测量中,限于测试条件,通常只能在上下层绕组间以及绕组端部处埋设PT100传感器,并根据PT100显示的测试数据来判断温升是否超限。在本文的算例电机中,在绕组槽内和绕组端部处各均布放置了6个PT100。
由于受到电网限制,算例电机在试验中限功率运行为2 MW,因而温升数据为2 MW发电下的测量数据,为了对比,在热路法进行计算时,也折算成2 MW功率下的发热量,因而计算数据与实测数据具有可比性,表3中可以看出,测试与计算数据偏差很小,基本在2度以内。
5 结论
本文以金风科技股份有限公司自主研发的 3 MW永磁同步发电机为实例,分别采用热路法和有限元方法对其在不同负载条件下的温度场进行了计算,并将计算结果与实测数据进行了对比,证明了热路法具有较高的精度,同时相比有限元法减少了计算量,可作为通风冷却方案设计初期的选型方法。
[1] 李文宇. 同步电机热计算与通风计算[J]. 船电技术,2007, 27(2): 72-75
[2] Juha Pyrho¨ nen, Tapani Jokinen and Vale´ ria Hrabovcova, Design of Rotating Electrical Machines[M]. John Wiley & Sons, Ltd, 2008.
[3] 陈志刚. 等效热网络法和有限元法在电机三维温度场计算中的应用与比较[J]. 中小型电机, 1995. 22(1):3-6, 35
[4] 李广德,何刚,何文秀.大型水轮发电机定子三维温度场计算[J]. 大电机技术, 2000, 4(2): 1-5.
[5] 熊斌,大型水轮发电机内部流体场和温度场的数值计算, 哈尔滨理工大学硕士学位论文: 2-4
[6] 李和明, 李俊卿. 电机中温度计算方法及其应用综述. 华北电力大学学报, 2005,32(1): 1-5
[7] 程福秀 林金铭. 现代电机设计[M]. 北京: 机械工业出版社.
[8] GB/T1993-1993,旋转电机冷却方法.
