基于DSP的PWM整流器控制系统研究

张骁 宋义超

（华中科技大学电气与电子工程学院，武汉 430074）

1 引言

PWM 整流器具有直流输出电压纹波小、输入端电流呈正弦、单位功率因数以及能量可双向流动等优点，对电网而言可视为一个纯阻性负载，极大地减少了电力电子变换装置对电网的谐波注入，是一种主动的抑制谐波的方法。近几十年来由于PWM整流器主电路并无多大突破，更多的研究集中在整流器的控制技术上，现在广泛采用的是在同步坐标系下电压、电流的双闭环控制策略，根据整流器的双环控制结构，采用DSP芯片，利用其内部资源和高速数据处理能力，研究了空间矢量脉宽调制的原理以及DSP实现算法，最后给出了实验结果及分析。

2 PWM整流器控制结构

三相电压型PWM整流器的主电路结构如图1所示，Ls为网侧滤波电感，C为直流滤波电容，RL为直流负载，ura,urb,urc为整流桥三相控制电压。

图1 电压型PWM整流器的主电路

采用坐标变换，从三相坐标系变换到两相同步坐标系下，得到在同步坐标下的方程：

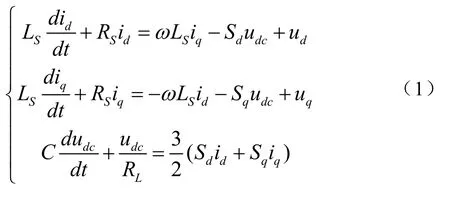
三相电压型PWM整流器目前应用最广泛、最为实用的控制方法是在同步坐标系下的电压、电流双闭环控制[1]。其控制原理为：输出直流电压与给定电压值的误差经过电压环的控制，输出作为有功电流指令。三相电源电流经同步坐标变换，得到有功电流和无功电流，无功电流的指令值由所需的功率因数角确定，若整流器运行于单位功率因数，则无功电流的指令值为零。 有功电流和无功电流实际值与其指令值经过电流解耦控制，得到整流桥中点控制电压，再经过空间矢量脉宽调制产生相应的PWM控制信号去驱动功率开关管的通断。在同步坐标系下，PWM 整流器的电压、电流双闭环控制结构框图如下图2所示：

图2 电压、电流双闭环控制框图

3 空间矢量脉宽调制的原理及其DSP实现

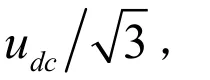
从三相电压型PWM整流器电路分析，六个开关管分别被 a, a’, b, b’, c, c’六个控制信号所控制，当整流器一个桥臂上的开关管开通时，对应的另一个开关管关闭。每相桥臂有两种开关模式，即上桥臂或下桥臂导通，因此整流器共有8种开关模式，用单极性二值逻辑开关函数Sj(j=a,b,c)描述，即：

空间电压矢量描述了三相PWM整流器整流桥交流侧相电压(ura, urb, urc)在复平面上的空间分布，由第二章所分析的，交流侧电压与开关函数和输出直流电压的关系为：

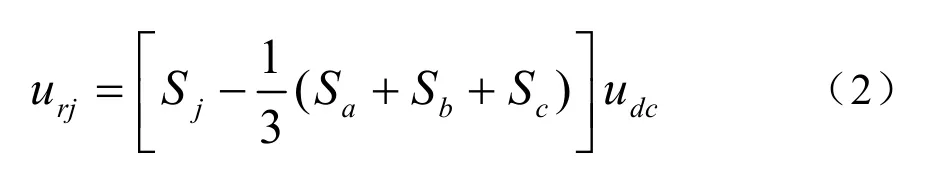
由坐标变换关系，从三相静止坐标系到两相静止坐标系，并考虑三相电压的平衡关系可得到：

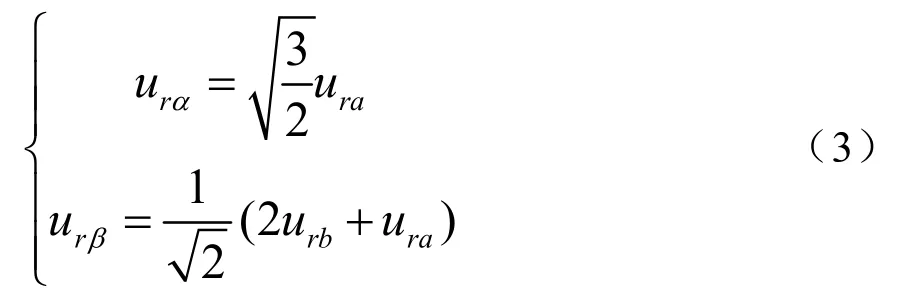
每个空间矢量与开关管的组合(c,b,a)相对应，例如：当(c,b,a)=001时，表示此时的空间矢量为U0，开关管的组合所决定的8个基本空间矢量如图3所示[4]：

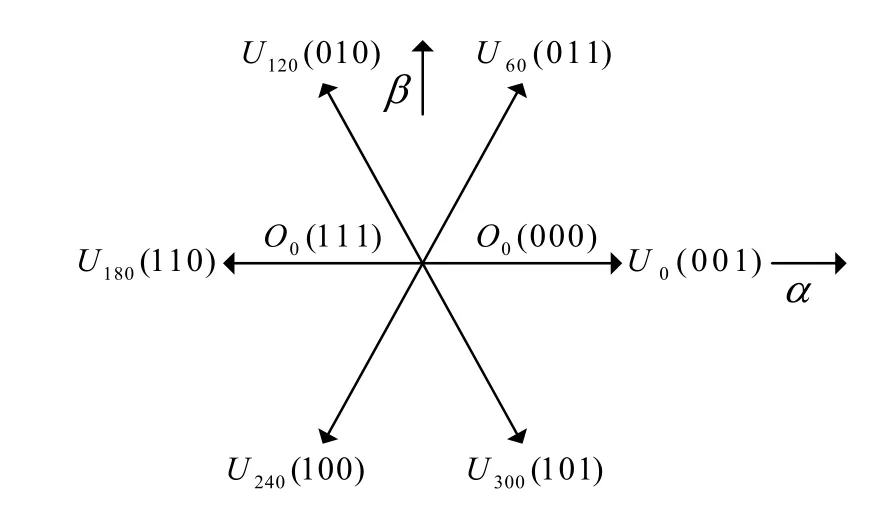
图3 基本空间矢量关系

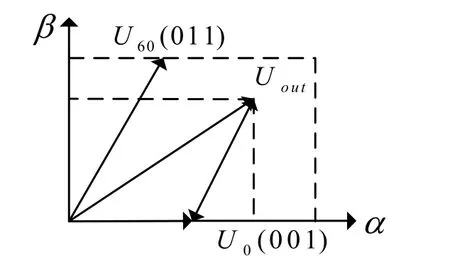
图4 坐标变换关系

空间矢量PWM的目的是通过与基本的空间矢量对应的开关组合得到一个给定的参考电压Uout，它的 α—β 轴分量分别用urα ,urβ表示。先考虑在第一扇区的情况，图4表示参考电压矢量Uout对应的urα ,urβ和基本空间矢量U0、U60的对应关系，有如下的表达式：

在图4中，Uout用U0、U60两个矢量来表示，有：

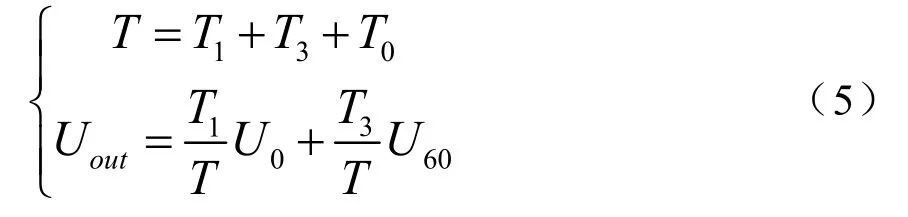
其中T1和T3分别是在周期时间T中基本空间矢量U0、U60各自作用的时间，T0是零矢量作用的时间。T1和T3可由下式计算：

同理，如果Uout位于被空间矢量U60、U120所包围的扇区2中，矢量作用时间的相对值也可表示为：

其中T2是空间矢量U120在周期中的作用时间。

为此，定义如下的X,Y,Z三个变量：

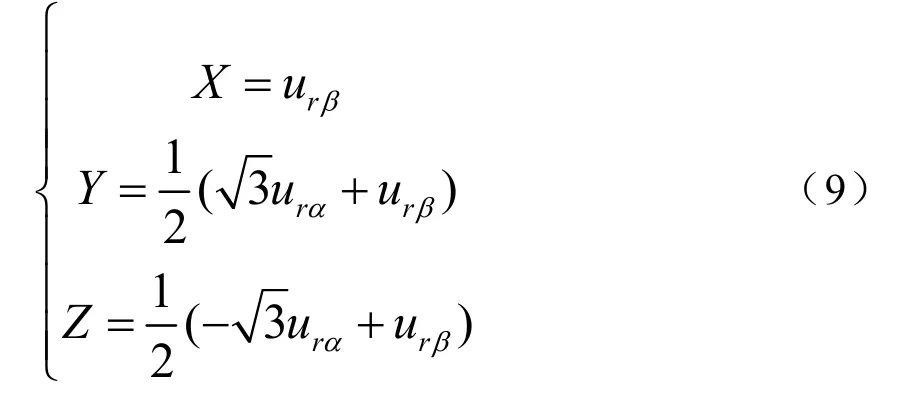
当Uou位于其他的空间矢量所包含的扇区中时，相应的t1,t2与X,Y,Z的对应关系为表1所示：

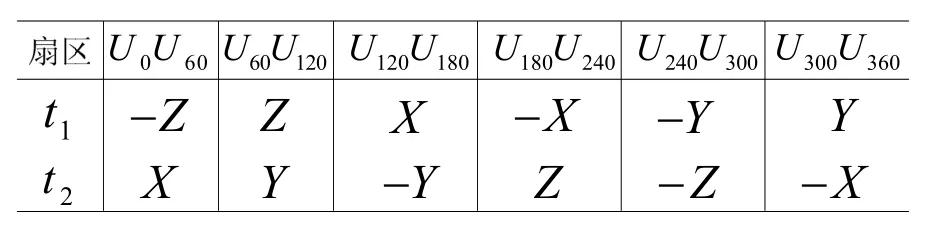
表1 t1,t2与X,Y,Z的对应关系

图5是当PWM控制周期为0.67 ms，正弦电压周期为20 ms时，TMS320LF2407输出的一路SVPWM波形。

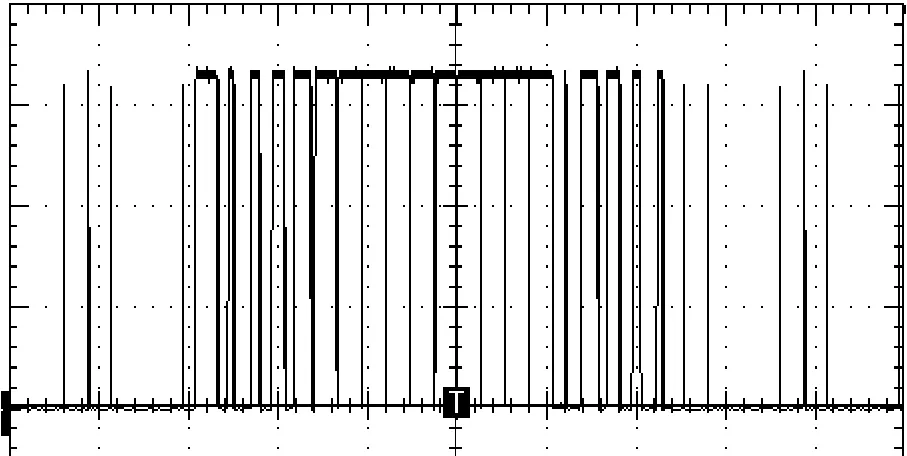
图5 DSP输出的一路SVPWM波形

程序设计需要在 DSP片内实现输入变量的采样、坐标变换、电压电流控制、空间矢量调制信号的运算等功能，系统的主程序框图如图6所示。数据处理子程序的框图如图7所示

图6 系统软件框图

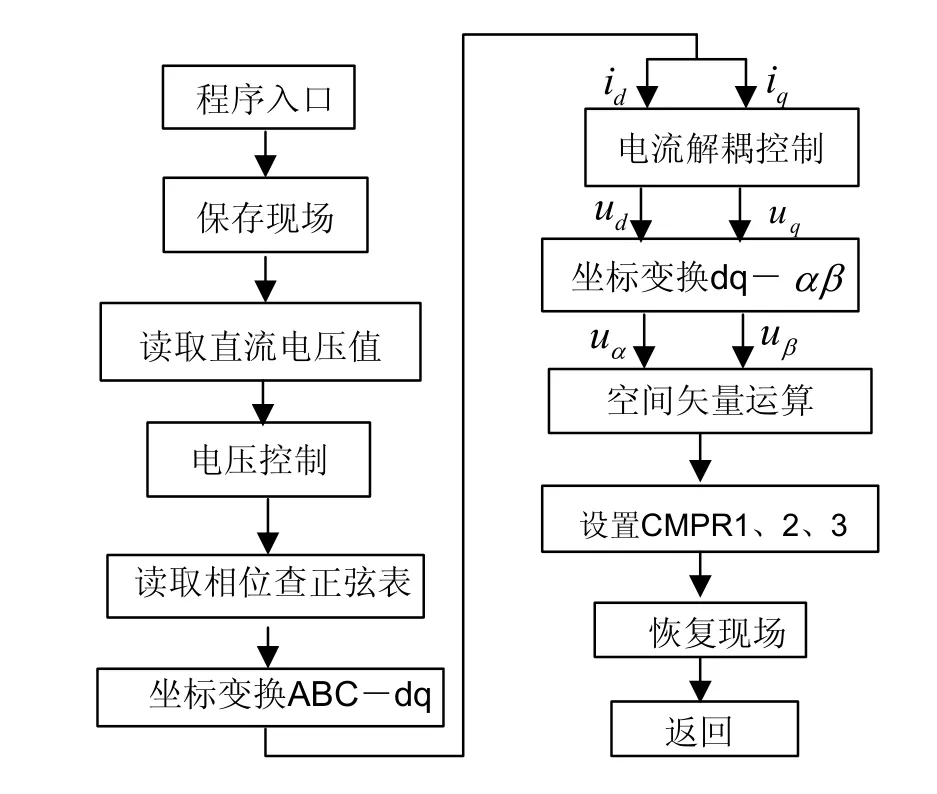
图7 数据处理程序框图

4 试验波结果及分析

图8是在1.5 kW纯阻性负载情况下，稳态时输出直流电压和a相输入电压、电流波形，可以看出，输出直流电压能很好地稳定在300 V，输入电流为正弦波，且与输入电压同相，基本上实现了单位功率因数。

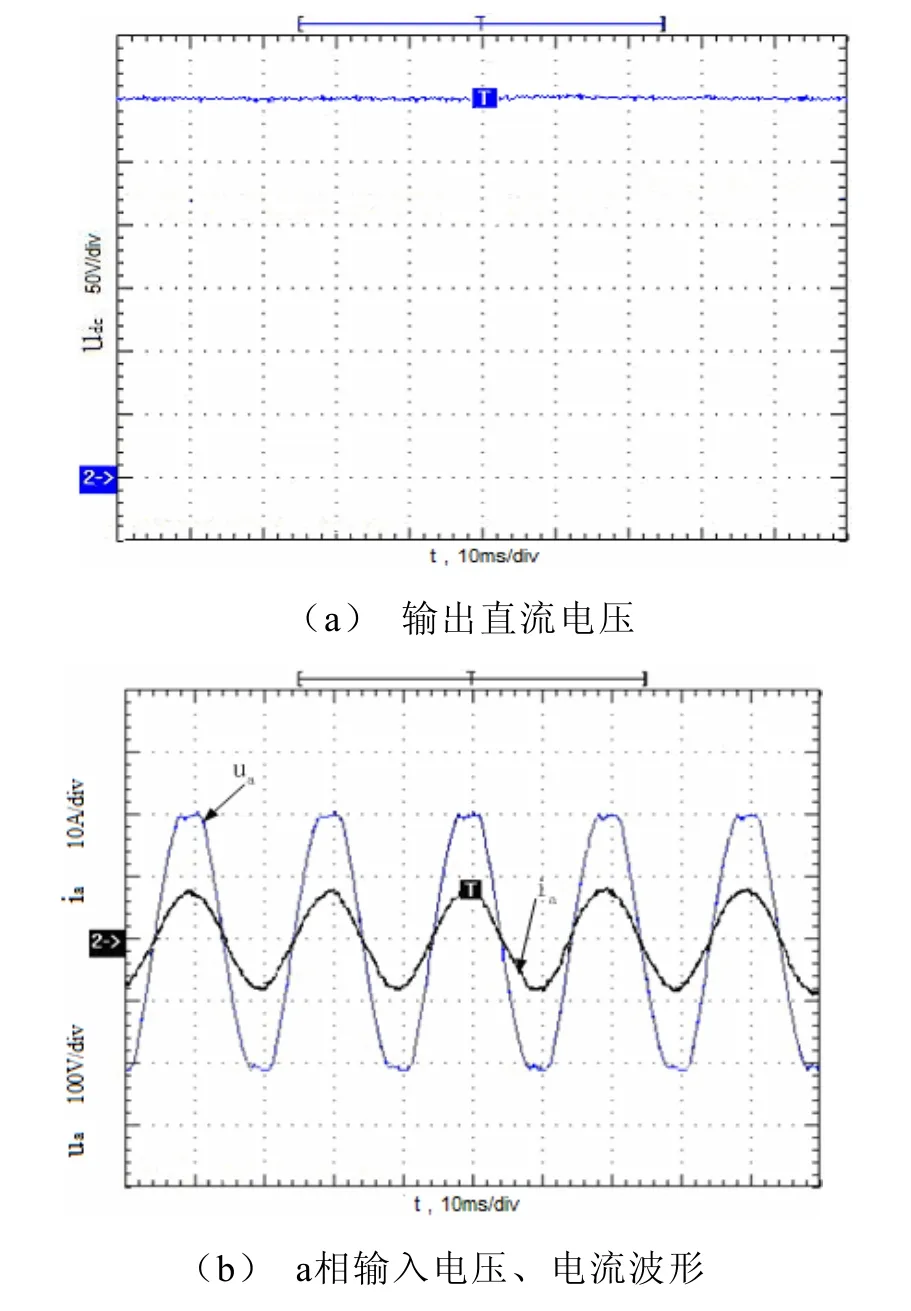
图8 PWM采用DSP控制时稳态波形

图9是在PWM整流器从空载突加1.5 kW纯阻性负载情况下，动态过程中输出电压和a相输入电压、电流的波形，输入电流也能很快地进入稳态，负载突变反应时间短，能很好地抗外部干扰。

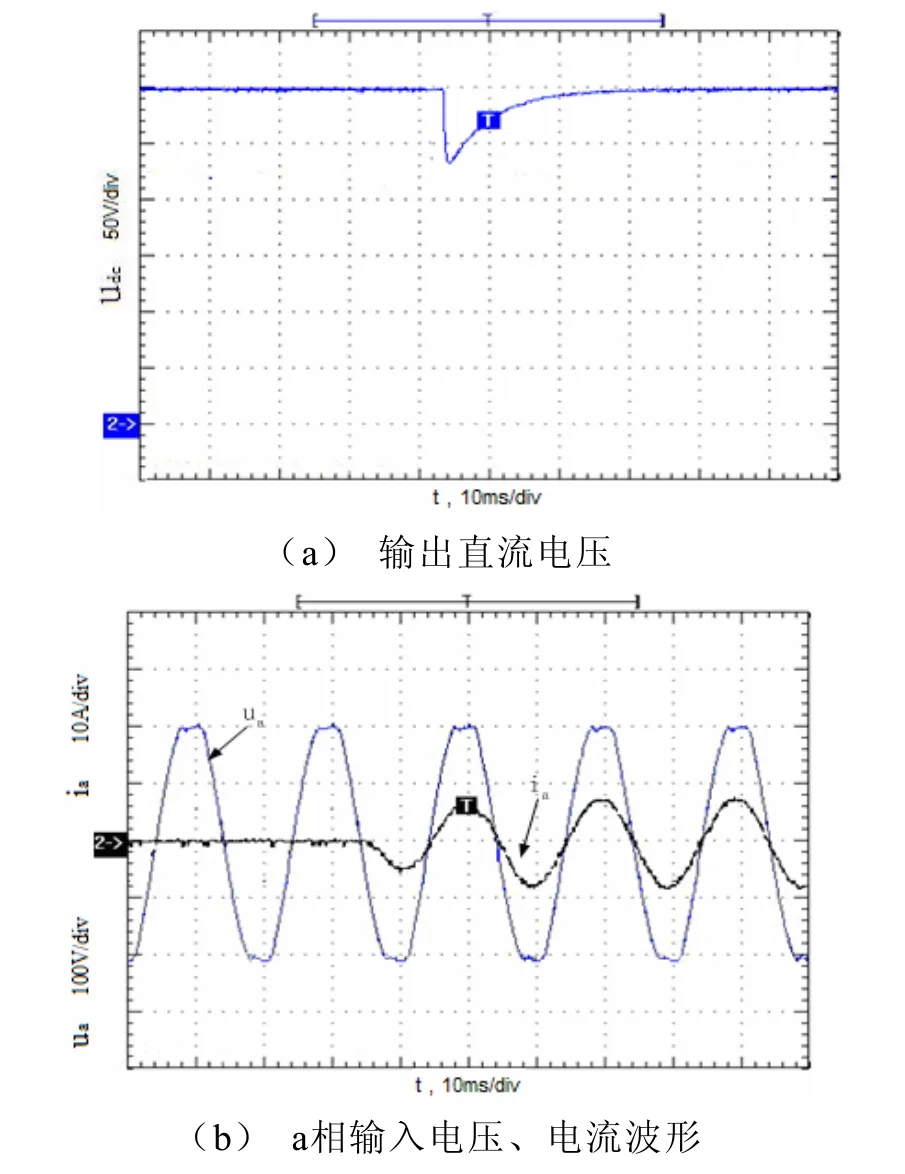
图9 PWM整流器负载突变调节时的波形

5 结论

本文介绍了PWM整流器的全数字化实现方法，采用在dq同步坐标系中的双闭环控制和空间矢量脉宽调制算法，实现了PWM整流器的单位功率因数，输出电压稳定、纹波小，在负载突变时能很快的进入稳定状态，具有一定的抗干扰能力。

[1] Ye Y, Kazerani M, Quintana V H..A novel modeling and control method for three-phase PWM converters. PESC.2001 IEEE 32th Annual, 2001.

[2] 张兴, 张崇巍. PWM 可逆变流器空间电压矢量控制技术研究. 中国电机工程学报, 2001, 21（10）.

[3] H. W. Van Der Broeck，H.C. Skudelny，G.V. Stanke.Analysis and realization of a pulse-width modulator based on voltage sapace vector. IEEE Trans.Ind Applicat, 1988, 24(1).

[4] 刘和平. MS320LF240x DSP结构、原理及应用. 北京: 北京航空航天大学出版社, 2002.